13.7.1. Свойства кодов

13.7.1.1. Длина кода и энтропия источника

13.7.2. Код Хаффмана

13.7.3. Групповые коды

13.7.3.1. Кодирование Хаффмана для факсимильной передачи

13.7.3.2. Коды Лемпеля-Зива (ZIP)

Кодирование с целью сокращения избыточности источника данных обычно влечет за собой выбор эффективного двоичного представления этого источника. Часто это требует замены двоичного представления символов источника альтернативным представлением. Замена обычно является временной и производится, для того чтобы достичь экономии при запоминании или передаче символов дискретного источника. Двоичный код, присвоенный каждому символу источника, должен удовлетворять определенным ограничениям, чтобы позволить обращение замены. К тому же код может быть далее ограничен спецификацией системы, например ограничениями памяти и простотой реализации.

Мы настолько привыкли к использованию двоичных кодов для представления символов источника, что можем забыть о том, что это всего лишь один из вариантов присвоения. Наиболее общим примером этой процедуры является двоичное присвоение количественным числительным (даже не будем рассматривать отрицательные числа). Можно прямо переводить в двоичную систему счисления, двоичные коды восьмеричных чисел, двоичные коды десятичных чисел, двоичные коды шестнадцате-ричных чисел, десятичные коды "два из пяти", десятичные коды с избытком три и т.д. В этом примере при выборе соответствия учитывается простота вычисления, определения ошибки, простота представления или удобство кодирования. Для определенной задачи сжатия данных основной целью является сокращение количества бит.

Конечные дискретные источники характеризуются множеством различных символов, Х(п), где п=1, 2,..., N — алфавит источника, a n - индекс данных. Полное описание требует вероятности каждого символа и совместных вероятностей символов, выбранных по два, три и т.д. Символы могут представлять двухуровневый (двоичный) источник, такой как черно-белые уровни факсимильного изображения, или многосимвольный источник, такой как 40 общих знаков санскрита. Еще одним общим многосимвольным алфавитом является клавиатура компьютерного терминала. Эти недвоичные символы отображаются посредством словаря, называемого знаковым кодом, в описание с помощью двоичного алфавита. (На рис. 2.2 представлен код ASCII, а на рис. 2.3 — код EBCDIC.) Стандартные знаковые коды имеют фиксированную длину, такую как 5-7 бит. Длина обычно выбирается так, чтобы существовало достаточно двоичных знаков для того, чтобы присвоить единственную двоичную последовательность каждому входному знаку алфавита. Это присвоение может включать большие и маленькие буквы алфавита, цифры, знаки пунктуации, специальные знаки и знаки управления, такие как знак забоя, возврата и т.д. Коды фиксированной длины обладают следующим свойством: знаковые границы отделены фиксированным числом бит. Это допускает превращение последовательного потока данных в параллельный простым счетом бит.

Двухкодовые стандарты могут определять один и тот же символ разными способами. Например, (7-битовый) код ASCII имеет достаточно бит, чтобы присвоить различные двоичные последовательности большой и маленькой версиям каждой буквы. С другой стороны, (5-битовый) код Бодо, который обладает только 32 двоичными последовательностями, не может сделать то же самое. Для подсчета полного множества знаков код Бодо определяет два контрольных знака, называемых переключением на печатание букв (letter shift — LS) и переключением на печатание цифр (figure shift — FS), которые должны использоваться как префиксы. При использовании эти контрольные знаки переопределяют отображение символа в двоичную форму. Это напоминает клавишу переключения регистра (shift key) на печатающем устройстве; эта клавиша полностью переопределяет новое множество символов на клавиатуре. Клавиатуры некоторых калькуляторов также имеют две клавиши переключения регистров, так что каждое нажатие клавиши имеет три возможных значения. Кроме того, некоторые команды текстового процессора используют двойные и тройные командные функции. В некотором смысле эти двух- и трехсловные команды представляют собой кодовое присвоение переменной длины. Эти более длинные кодовые слова присваиваются знакам (или командам), которые не встречаются так часто, как присвоенные отдельным кодовым словам. В обмен на использование соответствующих случаю более длинных слов получаем более эффективное запоминание (меньшая клавиатура) или более эффективную передачу источника.

Коды сжатия данных часто имеют переменную длину. Интуитивно ясно, что длина двоичной последовательности, присвоенной каждому символу алфавита, должна обратно зависеть от вероятности этого символа. Из всего сказанного очевидно, что если символ появляется с высокой вероятностью, он содержит мало информации и ему не должен выделяться значительный ресурс системы. Аналогично не будет казаться неразумным, что когда все символы одинаково вероятны, код должен иметь фиксированную длину. Возможно, наиболее известным кодом переменной длины является код (или азбука) Морзе (Morse code). Самуэль Морзе, чтобы определить относительную частоту букв в нормальном тексте, вычислил количество букв в шрифтовой секции печатающего устройства. Кодовое присвоение переменной длины отражает эту относительную частоту.

Если имеется существенное различие в вероятностях символов, может быть получено значительное сжатие данных. Чтобы достичь этого сжатия, необходимо достаточно большое число символов. Иногда, чтобы иметь достаточно большое множество символов, образуется новое множество символов, определенное из исходного множества и называемое кодом расширения. Эта процедура уже рассматривалась в примере 13.3, а общая технология будет изучена в следующем разделе.

13.7.1. Свойства кодов

Ранее обращалось внимание на свойства, которым должен удовлетворять полезный код. Некоторые из этих свойств являются очевидными, а некоторые — нет. Желаемые свойства стоят того, чтобы их перечислить и продемонстрировать. Рассмотрим следующий трехсимвольный алфавит со следующими вероятностными соответствиями.

Входному алфавиту сопутствуют следующие шесть двоичных кодовых соответствий, где крайний правый бит является наиболее ранним.

Изучите предлагаемые соответствия и попытайтесь определить, какие коды являются практичными.

Свойство единственности декодирования. Единственным образом декодируемые коды позволяют обратить отображение в исходный символьный алфавит. Очевидно, код 1 в предыдущем примере не является единственным образом декодируемым, так как символам а и b соответствует одна и та же двоичная последовательность. Таким образом, первым требованием полезности кода является то, чтобы каждому символу соответствовала уникальная двоичная последовательность. При этих условиях все другие коды оказываются удовлетворительными до тех пор, пока мы внимательно не изучим коды 3 и 6. Эти коды действительно имеют уникальную двоичную последовательность, соответствующую каждому символу. Проблема возникает при попытке закодировать последовательность символов. Например, попытайтесь декодировать двоичное множество 10111 при коде 3. Это b, a, b, b, b; b, a, b, с или b, а, с, b? Попытка декодировать ту же последовательность в коде 6 вызывает аналогичные сложности. Эти коды не являются единственным образом декодируемыми, даже если отдельные знаки имеют единственное кодовое соответствие.

Отсутствие префикса. Достаточным (но не необходимым) условием того, что код единственным образом декодируем, является то, что никакое кодовое слово не является префиксом любого другого кодового слова. Коды, которые удовлетворяют этому условию, называются кодами, свободными от префикса. Отметим, что код 4 не является свободным от префикса, но он единственным образом декодируем. Свободные от префикса коды также обладают таким свойством — они мгновенно декодируемы. Код 4 имеет свойство, которое может быть нежелательным. Он не является мгновенно декодируемым. Мгновенно декодируемый код — это такой код, для которого граница настоящего кодового слова может быть определена концом настоящего кодового слова, а не началом следующего кодового слова. Например, при передаче символа b с помощью двоичной последовательности 10 в коде 4, получатель не может определить, является ли это целым кодовым словом для символа b или частью кодового слова для символа с. В противоположность этому, коды 2 и 5 являются свободными от префикса.

13.7.1.1. Длина кода и энтропия источника

В начале главы были описаны формальные концепции информационного содержания и энтропии источника. Самоинформация символа Х_n в битах была определена следующим образом: I(Х_n)=log₂[1/P(X_n)]. С точки зрения того, что информация разрешает неопределенность, было осознано, что информационное содержание символа стремится к нулю, когда вероятность этого символа стремится к единице. Кроме того, была определена энтропия конечного дискретного источника как средняя информация этого источника. Поскольку информация разрешает неопределенность, энтропия является средним количеством неопределенности, разрешенной с использованием алфавита. Она также представляет собой среднее число бит на символ, которое требуется для описания источника. В этом смысле это также нижняя граница, которая может быть достигнута с помощью некоторых кодов сжатия данных, имеющих переменную длину. Действительный код может не достигать граничной энтропии входного алфавита, что объясняется множеством причин. Это включает неопределенность в вероятностном соответствии и ограничения буферизации. Средняя длина в битах, достигнутая данным кодом, обозначается как . Эта средняя длина вычисляется как сумма длин двоичных кодов, взвешенных вероятностью этих кодовых символов P(X_t).

Когда говорится о поведении кода переменной длины, массу информации можно получить из знания среднего числа бит. В кодовом присвоении переменной длины некоторые символы будут иметь длины кодов, превосходящие среднюю длину, в то время как некоторые будут иметь длину кода, меньшую средней. Может случиться, что на кодер доставлена длинная последовательность символов с длинными кодовыми словами. Кратковременная скорость передачи битов, требуемая для передачи этих символов, будет превышать среднюю скорость передачи битов кода. Если канал ожидает данные со средней скоростью передачи, локальный избыток информации должен заноситься в буфер памяти. К тому же на кодер могут быть доставлены длинные модели символов с короткими кодовыми словами. Кратковременная скорость передачи битов, требуемая для передачи этих символов, станет меньше средней скорости кода. В этом случае канал будет ожидать биты, которых не должно быть. По этой причине для сглаживания локальных статистических вариаций, связанных с входным алфавитом, требуется буферизация данных.

Последнее предостережение состоит в том, что коды переменной длины создаются для работы со специальным множеством символов и вероятностей. Если данные, поступившие на кодер, имеют существенно отличающийся перечень вероятностей, буферы кодера могут быть не в состоянии поддержать несоответствие и будет происходить недогрузка или перегрузка буфера.

13.7.2. Код Хаффмана

Код Хаффмана (Huffman code) [20] — это свободный от префикса код, который может давать самую короткую среднюю длину кода для данного входного алфавита. Самая короткая средняя длина кода для конкретного алфавита может быть значительно больше энтропии алфавита источника, и тогда эта невозможность выполнения обещанного сжатия данных будет связана с алфавитом, а не с методом кодирования. Часть алфавита может быть модифицирована для получения кода расширения, и тот же метод повторно применяется для достижения лучшего сжатия. Эффективность сжатия определяется коэффициентом сжатия. Эта мера равна отношению среднего числа бит на выборку до сжатия к среднему числу бит на выборку после сжатия.

Процедура кодирования Хаффмана может применяться для преобразования между любыми двумя алфавитами. Ниже будет продемонстрировано применение процедуры при произвольном входном алфавите и двоичном выходном алфавите.

Код Хаффмана генерируется как часть процесса образования дерева. Процесс начинается с перечисления входных символов алфавита наряду с их вероятностями (или относительными частотами) в порядке убывания частоты появления. Эти позиции таблицы соответствуют концам ветвей дерева, как изображено на рис. 13.34. Каждой ветви присваивается ее весовой коэффициент, равный вероятности этой ветви. Теперь процесс образует дерево, поддерживающее эти ветви. Два входа с самой низкой относительной частотой объединяются (на вершине ветви), чтобы образовать новую ветвь с их смешанной вероятностью. После каждого объединения новая ветвь и оставшиеся ветви переупорядочиваются (если необходимо), чтобы убедиться, что сокращенная таблица сохраняет убывающую вероятность появления. Это переупорядочение называется методом пузырька [21]. Во время переупорядочения после каждого объединения поднимается ("всплывает") новая ветвь в таблице до тех пор, пока она не сможет больше увеличиваться. Таким образом, если образуется ветвь с весовым коэффициентом 0,2 и во время процесса находятся две другие ветви уже с весовым коэффициентом 0,2, новая ветвь поднимается до вершины группы с весовым коэффициентом 0,2, а не просто присоединяется к ней. Процесс "всплытия" пузырьков к вершине группы дает код с уменьшенной дисперсией длины кода, в противном случае — код с такой же средней длиной, как та, которая получена посредством простого присоединения к группе. Эта сниженная дисперсия длины кода уменьшает шанс переполнения буфера.

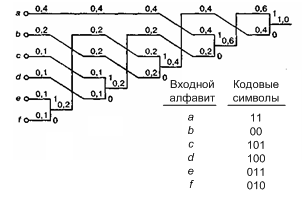
Рис. 13.34. Дерево кодирования Хаффмана для шестизначного множества

В качестве примера этой части процесса кодирования применим процедуру Хаффмана к входному алфавиту, изображенному на рис. 13.34. Протабулированный алфавит и связанные с ним вероятности изображены на рисунке. После формирования дерева, чтобы различать две ветви, каждая вершина ветви снабжается двоичным решением "1/0". Присвоение является произвольным, но для определенности на каждой вершине будем обозначать ветвь, идущую вверх как "1", и ветвь, идущую вниз как "0". После обозначения вершин ветвей проследим траектории дерева от основания (крайнее правое положение) до каждой выходной ветви (крайнее левое положение). Траектория — это двоичная последовательность для достижения этой ветви. В следующей таблице для каждого конца ветви указана последовательность, соответствующая каждой траектории, где i = 1,..., 6.

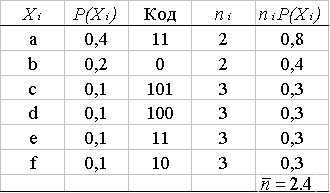
Находим, что средняя длина кода п для этого алфавита равна 2,4 бит на знак. Это не означает, что необходимо найти способ передачи нецелого числа бит. Это означает, что для передачи 100 входных символов через канал связи в среднем должно пройти 240 бит. Для сравнения, код фиксированной длины, требуемый для охвата шестизначного входного алфавита, должен иметь длину 3 бит и энтропию входного алфавита (используем формулу (13.32)), равную 2,32 бит. Таким образом, этот код дает коэффициент сжатия 1,25 (3,0/2,4) и достигает 96,7% (2,32/2,40) возможного коэффициента сжатия. В качестве еще одного примера рассмотрим случай, для которого можно продемонстрировать использование кода расширения. Изучим трехзначный алфавит, представленный в разделе 13.6.1.

Дерево кода Хаффмана для этого алфавита изображено на рис. 13.35, а его элементы протабулированы ниже.

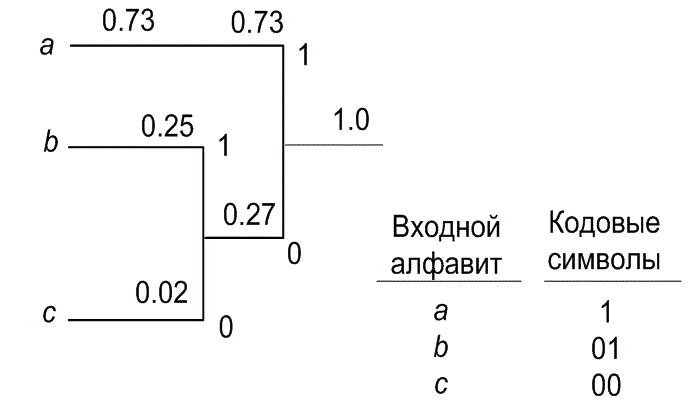
Рис. 13.35. Дерево кодирования Хаффмана для трехзначного множества

Здесь i = 1, 2, 3. Средняя длина кода в приведенном примере равна 1,31 бит; она будет равна 2 бит для кода Хаффмана фиксированной длины. Коэффициент сжатия для этого кода равен 1,53. И снова, используя равенство (13.32), получим, что энтропия для алфавита равна 0,9443 бит, так что эффективность кода (0,944/1,31 = 72%) значительно меньше, чем для предыдущего примера.

Чтобы улучшить эффективность кодирования или достичь большего сжатия, следует переопределить алфавит источника. Больший алфавит источника увеличивает разнообразие, что является одним из требований при сокращении средней длины кода и увеличении числа ветвей дерева для присвоения кода переменной длины. Это делается посредством выбора знаков (по два) из алфавита источника, которые становятся новыми знаками в расширенном алфавите. Если предположить, что .символы независимы, вероятность каждого нового элемента является произведением отдельных вероятностей. Алфавит расширения имеет следующий вид.

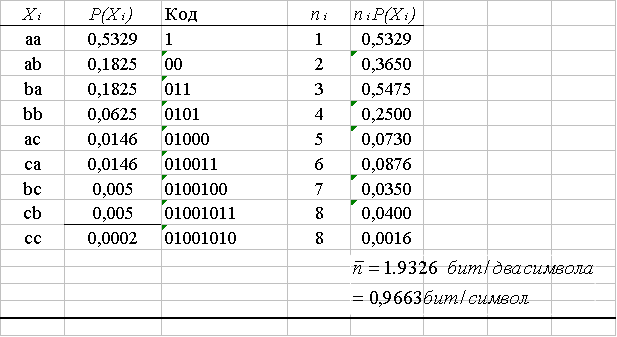
Здесь i — 1, ..., 9, а кодовая последовательность для каждого X_i была найдена с использованием выше приведенной процедуры Хаффмана. Коэффициент сжатия для этого кода расширения равен 2,076, а эффективность кодирования — 97,7%. Коды расширения предлагают очень мощную технологию включения эффектов множеств символов, которые не являются независимыми. Например, в английском алфавите соседние буквы являются высоко коррелированными. Очень часто встречаются следующие пары букв.

Здесь подчеркивание представляет пробел. Наиболее общими английскими наборами трех букв являются следующие.

Таким образом, вместо того чтобы производить кодирование Хаффмана отдельных букв, более эффективно расширить алфавит, включив все 1-кортежи плюс распространенные 2-и 3-кортежи, а затем произвести кодирование с помощью кода расширения.

13.7.3. Групповые коды

Во многих приложениях последовательность символов, которую необходимо передать или запомнить, характеризует последовательное кодирование определенных символов. Иногда, вместо того чтобы кодировать каждый символ последовательности, есть смысл описать группу с помощью подстановочного кода. В качестве примера рассмотрим случай, когда последовательности пробелов (наиболее употребимый символ в тексте) кодируются во многих протоколах связи с помощью символа управления, за которым следует счетчик символов. Протокол IBM 3780 BISYNC имеет опцию замены последовательности пробелов с помощью знака "IGS" (если имеем дело с EBCDIC) или "GS" (если имеем дело с ASCII), за которым следует счетчик от 2 до 63. Более длинные последовательности делятся на серии по 63 знака.

Групповое подстановочное кодирование может быть применено к исходному алфавиту символов или двоичному представлению этого алфавита. В частности, групповое кодирование является удачным для двоичных алфавитов, полученных от специфических источников. Наиболее важным коммерческим примером является факсимильное кодирование, используемое для передачи документов по мгновенной электронной почте [22].

13.7.3.1. Кодирование Хаффмана для факсимильной передачи

Факсимильная передача — это процесс передачи двухмерного образа как последовательности последовательных строчных разверток. В действительности наиболее распространенными образами являются документы, содержащие текст и цифры. Положение строчной развертки и положение вдоль развертки квантуются в пространственные расположения, которые определяют двухмерную координатную сетку элементов картинки, называемых пикселями. Ширина стандартного документа МККТТ определяется равной 8,27 дюймов (20,7 см ), а длина— 11,7 дюймов (29,2 см), почти 8,5 дюймов на 11,0 дюймов. Пространственное квантование для нормального разрешения составляет 1728 пикселей/строку и 1188 строк/документ. Стандарт также определяет квантование с высоким разрешением с теми же 1728 пикселями/строку, но с 2376 строками/документ. Общее число отдельных пикселей для факсимильной передачи с нормальным разрешением составляет 2 052 864, и оно удваивается для высокого разрешения. Для сравнения, число пикселей в стандарте NTSC (National Television Standards Committee — Национальный комитет по телевизионным стандартам) коммерческого телевидения составляет 480 х 460, или 307 200. Таким образом, факсимильное изображение имеет разрешение в 6,7 или 13,4 раза больше разрешения стандартного телевизионного образа.

Относительная яркость или затемненность развернутого образа в каждом положении на строке развертки квантуется в два уровня: Ч (черный) и Б (белый). Таким образом, сигнал, наблюдаемый на протяжении линии развертки, — это двухуровневая модель, представляющая элементы Ч и Б. Легко видеть, что горизонтальная развертка данной страницы будет представлять последовательность, состоящую из длинных групп уровней Ч и Б. Стандарт МККТТ схемы группового кодирования для сжатия отрезков Ч и Б уровней базируется на модифицированном коде Хаффмана переменной длины, который приведен в табл. 13.1. Определяются два типа шаблонов, группы Б и Ч. Каждый отрезок описывается кодовыми словами деления. Первое деление, названное созданное кодовое слово, определяет группы с длинами, кратными 64. Второе деление, именуемое оконечное кодовое слово, определяет длину оставшейся группы. Каждая серия из знаков Ч (или Б), длиной от 0 до 63, обозначает единственное кодовое слово Хаффмана, как и каждая группа длины 64К, где К= 1, 2, ..., 27. Также кодом определен уникальный символ конца строки (end of line — EOL), который указывает, что дальше не следуют черные пиксели. Следовательно, должна начаться следующая строка, что подобно возврату каретки пишущей машинки [23].

Таблица 13.1. Модифицированный код Хаффмана для стандарта

Длина группы	Белые		Черные		Длина группы	Белые	Черные
Созданные кодовые слова
64 128 192 256 320 384 448 512 576 640 704 768 832 896		11011 10010 010111 0110111 00110110 00110111 01100100 01100101 01101000 01100111 011001100 011001101 011010010 011010011		0000001111 000011001000 000011001001 000001011011 000000110011 000000110100 000000110101 0000001101100 0000001101101 0000001001010 0000001001011 0000001001100 0000001001101 0000001110010	960 1024 1088 1152 1216 1280 1344 1408 1472 1536 1600 1664 1728 EOL	011010100 011010101 011010110 011010111 011011000 011011001 011011010 011011011 010011000 010011001 010011010 011000 010011011 000000000001	0000001110011 0000001110100 0000001110101 0000001110110 0000001110111 0000001010010 0000001010011 0000001010100 0000001010101 0000001011010 0000001011011 0000001100100 000000110010J 000000000001
Длина группы		Белые		Черные	Длина группы	Белые	Черные
Созданные кодовые слова
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18		00110101 000111 0111 1000 1011 1100 1110 1111 10011 10100 00111 01000 001000 000011 110100 110101 101010 101011 0100111		000110111 010 11 10 011 ООП 0010 00011 000101 000100 0000100 0000101 0000111 00000100 00000111 000011000 0000010111 0000011000 0000001000	32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50	00011011 00010010 00010011 00010100 00010101 00010110 00010111 00101000 00101001 00101010 00101011 00101100 00101101 00000100 00000101 00001010 00001011 01010010 01010011	000001101010 000001101011 000011010010 000011010011 000011010100 000011010101 000011010110 000011010111 000001101100 000001101101 000011011010 000011011011 000001010100 000001010101 000001010110 000001010111 000001100100 000001100101 000001010010
Длина группы		Белые		Черные	Длина группы	Белые	Черные
Созданные кодовые слова
19 20 21 22 23 24 25 26 27 28 29 30 31		0001100 0001000 0010111 0000011 0000100 0101000 0101011 0010011 0100100 0011000 00000010 00000011 00011010		00001100111 00001101000 00001101100 00000110111 00000101000 00000010111 00000011000 000011001010 000011001011 000011001100 000011001101 000001101000 000001101001	51 52 53 54 55 56 57 58 59 60 61 62 63	01010100 01010101 00100100 00100101 01011000 01011001 01011010 01011011 01001010 01001011 00110010 00110011 00110100	000001010011 000001000100 000000110111 000000111000 000000100111 000000101000 000001011000 000001011001 000000101011 000000101100 000001011010 000001100110 000001100111

Пример 13.8. Код группового кодирования

Используйте модифицированный код Хаффмана для сжатия строки

200 Б, 10 Ч, 10 Б, 84 Ч, 1424 Б,

состоящей из 1728 пиксельных элементов.

Решение

Используя табл. 13.1, определим, каким должно быть кодирование для этой модели (для

удобства чтения введены пробелы).

Итак, требуется всего 56 бит, чтобы послать эту строку, содержащую последовательность 1188 бит.

13.7.3.2. Коды Лемпеля-Зива (ZIP)

Основной сложностью при использовании кода Хаффмана является то, что вероятности символов должны быть известны или оценены и как кодер, так и декодер должны знать дерево кодирования. Если дерево строится из необычного для кодера алфавита, канал, связывающий кодер и декодер, должен также отправлять кодирующее дерево как заголовок сжатого файла. Эти служебные издержки уменьшат эффективность сжатия, реализованную с помощью построения и применения дерева к алфавиту источника. Алгоритм Лемпеля-Зива (Lempel-Ziv) и его многочисленные разновидности используют текст сам по себе для итеративного построения синтаксически выделенной последовательности кодовых слов переменной длины, которые образуют кодовый словарь.

Код предполагает, что существующий словарь содержит уже закодированные сегменты последовательности символов алфавита. Данные кодируются с помощью просмотра существующего словаря для согласования со следующим коротким сегментом кодируемой последовательности. Если согласование найдено, код следует такой философии: поскольку получатель уже имеет этот сегмент кода в своей памяти, нет необходимости пересылать его, требуется только определить адрес, чтобы найти сегмент. Код ссылается на расположение последовательности сегмента и затем дополняет следующий символ в последовательности, чтобы образовать новую позицию в словаре кода. Код начинается с пустого словаря, так что первые элементы являются позициями, которые не ссылаются на более ранние. В одной, форме словаря рекуррентно формируется выполняемая последовательность адресов и сегмент символов алфавита, содержащийся в ней. Закодированные данные состоят из пакета <адрес словаря, следующий знак данных>, а каждый новый входной элемент словаря образован как пакет, содержащий адрес того словаря, за которым следует следующий символ. Рассмотрим пример такой технологии кодирования.

Закодируйте последовательность символов [a b a a b a b b b b b b b a b b b b a]

Закодированные пакеты:	<0,а>, <0,b>, <l,a>, <2,a>, <2,b>, <5,b>, <5,a>, <6,b>, <4,->
Адрес: Содержимое:	1 a	2 b	3 aa	4 ba	5 bb	6 bbb	7 bba	8 bbbb

Начальный пакет <0,а> показывает нулевой адрес, потому что в словаре еще нет ни одной позиции. В этом пакете знак "а" является первым в последовательности данных, и он приписан к адресу 1. Следующий пакет <0,b> содержит второй знак данных b, который еще не был в словаре (следовательно, адресное значение есть 0); b приписывается адресу 2. Пакет <1,а> представляет кодирование следующих двух знаков "аа" с помощью вызова адреса 1 для первого и присоединения к этому адресу следующего знака "а". Пара знаков "аа" приписывается адресу 3. Пакет <2,а> представляет кодирование следующих двух знаков данных "bа" с помощью вызова адреса 2 для знака "b" и присоединения к этому адресу следующего знака "а". Пара знаков данных "bа" приписывается адресу 4 и т.д. Отметим, как завершается групповое кодирование. Восьмой пакет составлен из адреса 6, содержащего три знака "b", за которыми следует другой знак "b". В этом примере закодированные данные могут быть описаны с помощью трехбитового адреса с последующим битом 0 или 1 для определения присоединенного знака. В закодированной последовательности существует последовательность из 9 символов для общего содержимого в 36 бит для кодирования данных, содержащих 20 знаков. Как во многих схемах сжатия, эффективность кодирования не достигается для коротких последовательностей, как в этом примере, и имеется только для длинных последовательностей.

В другой форме алгоритма Лемпеля-Зива закодированные данные представлены как три словесных пакета вида <число знаков сзади, длина, следующий знак>. Здесь концепция адреса не используется. Наоборот, имеются ссылки на предшествующие последовательности данных, а также допускаются рекуррентные ссылки на параметр длины. Это показано в следующем примере, представленном как позиция <1,7,а>.

Закодируйте последовательность символов [a b a a b a b b b b b b b a b b b b b a]

Здесь также не видно эффективности кодирования для короткой серии данных. Разновидности кода ограничивают размер обратной ссылки, например 12-битовая для максимума в 4 096 пунктов обратной ссылки. Это ограничение уменьшает размер памяти, требуемой для словаря, и сокращает вероятность перегрузки памяти. Возможны также модификации кода, ограничивающие длину префикса или фразы, определенной первыми двумя аргументами <назад n1, вперед п2, ххх>, которые должны быть меньше некоторого значения (например, 16) с целью ограничения сложности обратного поиска во время кодирования. Алгоритм Лемпеля-Зива присутствует во многих коммерческих и пробных программах, которые включают сжатие LZ77, Gzip, LZ78, LZW и UNIX.