Обычно способ передачи (способ кодирования и модуляции) задан и нужно определить помехоустойчивость, которую обеспечивают различные способы приема. Какой из возможных способов приема является оптимальным? Указанные вопросы являются предметом рассмотрения теории помехоустойчивости, основы; которой разработаны академиком В. А. Котельниковым.

Помехоустойчивостью системы связи называется способность системы различать (восстанавливать) сигналы с заданной достоверностью.

Задача определения помехоустойчивости всей системы в целом весьма сложная. Поэтому часто определяют помехоустойчивость отдельных звеньев системы: приемника при заданном способе передачи, системы кодирования или системы модуляции при заданном способе приема и т. д.

Предельно достижимая помехоустойчивость называется, по Котельникову, потенциальной помехоустойчивостью. Сравнение потенциальной и реальной помехоустойчивости устройства позволяет дать оценку качества реального устройства и найти еще неиспользованные резервы. Зная, например, потенциальную помехоустойчивость приемника, можно судить, насколько близка к ней реальная помехоустойчивость существующих способов приема и насколько целесообразно их дальнейшее усовершенствование при заданном способе передачи.

Сведения о потенциальной помехоустойчивости приемника при различных способах передачи позволяют сравнить эти способы передачи между собой и указать, какие из них в этом отношении являются наиболее совершенными.

При отсутствии помех каждому принятому сигналу х соответствует вполне определенный сигнал s. При наличии помех это однозначное соответствие нарушается. Помеха, воздействуя на передаваемый сигнал, вносит неопределенность относительно того, какое из возможных сообщений было передано, и по принятому сигналу х только с некоторой вероятностью можно судить о том, что был передан тот или иной сигнал s. Эта неопределенность описывается апостериорным распределением вероятностей P(s/x).

Если известны статистические свойства сигнала s и помехи w, то можно создать приемник, который на основании анализа сигнала х будет находить апостериорное распределение P(s/x). Затем по виду этого распределения принимается решение о том, какое из возможных сообщений было передано. Решение принимается оператором или самим приемником по правилу, которое определяется заданным критерием.

Задача состоит в том, чтобы воспроизвести передаваемое сообщение наилучшим образом в смысле выбранного критерия. Такой приемник называется оптимальным, а его помехоустойчивость будет максимальной при заданном способе передачи.

Несмотря на случайный характер сигналов х, в большинстве случаев имеется возможность выделить множество наиболее вероятных сигналов соответствующих передаче некоторого сигнала st. Геометрическое представление позволяет множество сигналов заменить областью многомерного пространства.

Пусть область X принимаемых сигналов разбита на неперекрывающиеся области причем каждому сигналу sсоответствует область Х. Если принятый сигнал попал в эту область, то приемник принимает решение о том, что передавался сигнал s С некоторой вероятностью сигнал Xi может попасть в любую другую область , и тогда принимается ошибочное решение: вместо сигнала s, воспроизводится сигнал . Вероятность того, что переданный сигнал принят правильно, равна , а вероятность того, что он принят ошибочно, равна . Условная вероятность ) зависит от способа формирования сигнала, от помех, имеющихся в канале, и от выбранной решающей схемы приемника. Полная вероятность ошибочного приема элемента сигнала, очевидно, будет равна:

(5.1)

где — априорные вероятности передаваемых сигналов.

В случае двоичного канала область принимаемых сигналов разбивается на две области X и Xz. Если сигнал х попадает в область X , то воспроизводится сигнал, а если в область X, то — s2.

В канале последовательность элементов входного сообщения u(t) преобразовывается в последовательность элементов выходного сообщения v(t). В геометрическом представлении это означает преобразование пространства входных сообщений U в пространство выходных сообщений V. При изучении каналов иногда удобно рассматривать вместо элементов исходного сообщения последовательность кодовых символов.

Канал называется дискретным, если входные и выходные пространства (сообщения) дискретны, и непрерывным, если эти пространства непрерывны. Если одно из пространств дискретно, а другое — непрерывно, то канал называется соответственно дискретно-непрерывным или непрерывно-дискретным.

Свойства дискретного канала определены, если заданы: алфавиты входных кодовых символов и выходных , скорость передачи символов V и вероятности переходов т. е. вероятности того, что принят символ , когда был передан символ ,-. В общем случае и символы могут отличаться по своей природе от символов , . Например, звуки речи, составляющие входной алфавит при телефонной передаче, могут воспроизводиться на приемном конце не только в виде звука, но и в виде текста, записанного на пленку.

Если вероятности переходов Р(/) для каждой пары i, j не зависят от времени и от того, какие символы передавались и принимались ранее, то такой канал называется однородным без памяти. Если эти вероятности зависят от времени, то канал называется неоднородным, а если они зависят от того, какие символы передавались и принимались ранее, то канал называется каналом с памятью. Математическим описанием канала с памятью является дискретная цепь Маркова.

Если в однородном канале алфавиты кодовых символов на входе и выходе одинаковы и для любой пары вероятности переходов постоянны , то такой канал называется симметричным (рис. 5.1а).

Среди каналов, в которых алфавиты на входе и выходе неодинаковы, представляет интерес так называемый стирающий канал,

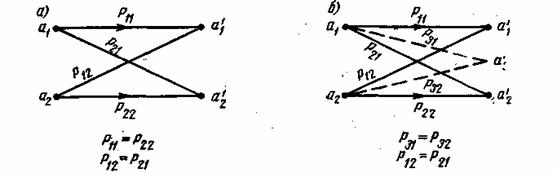
Рис. 5.1. Графическое представление работы однородного бинарного канала: симметричный канал (а), канал со стиранием (б)

в котором . В таком канале выходной алфавит содержит дополнительный символ обозначающий «стирание». Появление этого символа на выходе означает, что переданный символ искажен помехами и не может быть опознан. Как будет показано в дальнейшем, введение такого стирающего символа облегчает возможность правильного декодирования принятой кодовой комбинации. Геометрическое представление стирающего канала дано на рис. 5.16. В канале без помех каждому входному символу однозначно соответствует символ a'k на выходе (вероятности неправильных переходов равны нулю).