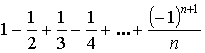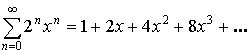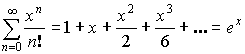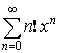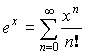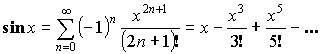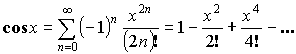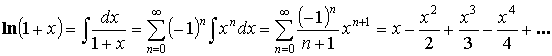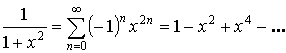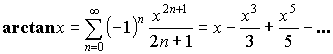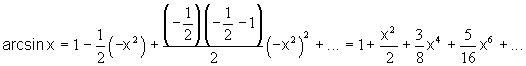9.1. Числовые ряды
Сходимость ряда. Сумма ряда
Пусть даны ![]() , тогда
, тогда 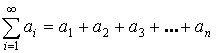 – ряд, где
– ряд, где ![]() – член ряда.
– член ряда.
Примеры различных рядов:
- 1+2+4+…+
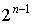 – ряд сходится.
– ряд сходится. - 1–1+1–1+…+
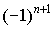 – расходится.
– расходится.
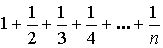 – расходится (гармонический ряд).
– расходится (гармонический ряд).
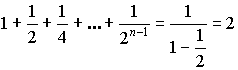 - сходится.
- сходится.
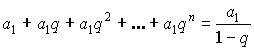 , при
, при ![]() .
.
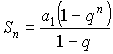
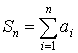 – частичная сумма
– частичная сумма
Если ![]() , то
, то ![]() – сумма ряда. Ряд сходится, если этот предел существует, и расходится, если не существует.
– сумма ряда. Ряд сходится, если этот предел существует, и расходится, если не существует.
Пример:
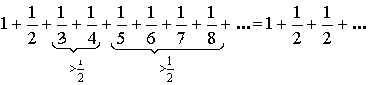
![]()
Теорема. О сходимости ряда
Сходимость ряда не измениться, если отбросить конечное число его членов.
Признаки сходимости ряда
- Необходимый признак сходимости:
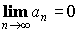
- Достаточный признак расходимости:
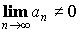
Доказательство:
![]()
![]()
![]()
Если ![]() , то ряд сходится.
, то ряд сходится.
-
- Достаточный признак сходимости (для знакопостоянных рядов):
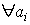
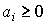
- Признак сравнения:
- Достаточный признак сходимости (для знакопостоянных рядов):
Имеем ![]() и
и ![]() , то
, то
![]()
![]() и
и ![]() – сходится, тогда
– сходится, тогда ![]() – сходится.
– сходится.
![]() или
или ![]() .
.
Если 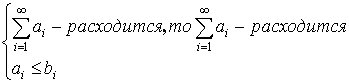
Пример:
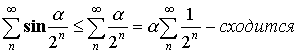 , а значит
, а значит 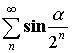 – сходится.
– сходится.
-
- Признак Даламбера:
Пусть 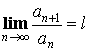 , тогда при
, тогда при
![]() – ряд сходится,
– ряд сходится, ![]() – ряд расходится,
– ряд расходится, ![]() – требуются дальнейшие исследования.
– требуются дальнейшие исследования.
Доказательство:
Пусть ![]() , тогда
, тогда ![]() , начиная с некоторого
, начиная с некоторого ![]() .
.
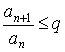
![]() или
или ![]()
Получаем 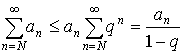
Пример:
Ряд – ![]()
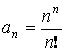 и
и 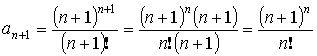
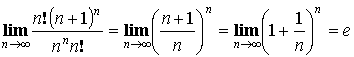 – ряд расходится.
– ряд расходится.
- Радикальный признак Коши:
![]() , при
, при ![]() ,
, ![]() .
.
Тогда если ![]() , то ряд сходится, если
, то ряд сходится, если ![]() – ряд расходится.
– ряд расходится.
Доказательство:
-
- Пусть
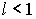 и
и 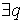
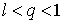
- Пусть
Тогда, начиная с некоторого ![]() ,
, ![]() , выполняется неравенство
, выполняется неравенство ![]() или
или ![]() .
.
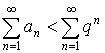
![]() – сходится (бесконечно убывающая геометрическая прогрессия), а значит
– сходится (бесконечно убывающая геометрическая прогрессия), а значит ![]() –сходится по принципу сравнения.
–сходится по принципу сравнения.
- Пусть
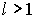 и
и 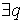
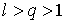
Тогда, начиная с некоторого ![]() ,
, ![]() , выполняется неравенство
, выполняется неравенство ![]() или
или ![]() .
.
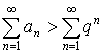
Получаем, что ![]() –расходится.
–расходится.
Пример:
Ряд – ![]() .
.
Получаем 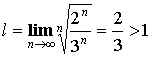 – ряд сходится.
– ряд сходится.
- Интегральный признак Коши:
![]() , при
, при ![]() .
.
![]()
![]()
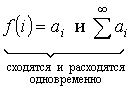
Доказательство:
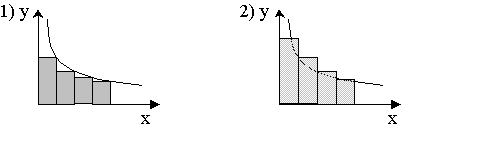
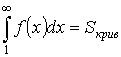 и
и 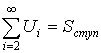
![]()
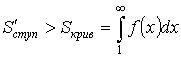
Значит, если ![]() – сходится
– сходится 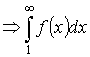 – сходится.
– сходится.
Знакочередующиеся ряды
Ряды вида: ![]() , где
, где ![]() .
.
Теорема Лейбница
Если ![]() и
и ![]() , то ряд
, то ряд 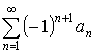 – сходится.
– сходится.
Доказательство:
Пусть ![]() , тогда
, тогда
![]() . При
. При ![]()
![]() .
. ![]() ограниченна сверху
ограниченна сверху ![]() .
.
Так как ![]() – возрастает и ограниченна сверху
– возрастает и ограниченна сверху ![]()
Пример: ![]() – сходится.
– сходится.
Пусть дан ряд ![]() , тогда
, тогда
-
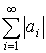 – сходится, тогда ряд – абсолютно сходится.
– сходится, тогда ряд – абсолютно сходится.
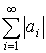 – расходится и
– расходится и 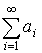 – сходится, тогда ряд сходится условно.
– сходится, тогда ряд сходится условно.
Теорема. Если ряд абсолютно сходится, то любая перестановка членов не меняет сумму.
Если ряд сходится условно, то подходящей перестановкой можно сделать его сумму равной любому числу и даже сделать его расходящимся.
Действия над рядами
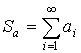 ,
, 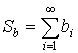 – абсолютно сходящиеся.
– абсолютно сходящиеся.
Тогда 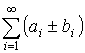 – абсолютно сходится.
– абсолютно сходится.
Функциональные ряды
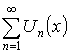 , где
, где ![]() – функция.
– функция.
Область сходимости
Пусть ![]() фиксировано.
фиксировано.
Тогда 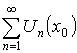 сходится, если
сходится, если ![]() –точка сходимости, и расходится, если
–точка сходимости, и расходится, если ![]() – точка расходимости.
– точка расходимости.
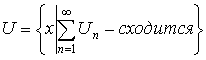 – область сходимости.
– область сходимости.
Пример:
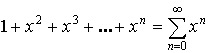
![]() , то ряд сходится.
, то ряд сходится.
![]()
![]() , где
, где ![]() – остаток ряда.
– остаток ряда.
Если ряд сходится, то ![]()
Мажорируемые ряды
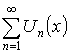 , где
, где ![]() – мажорируемы.
– мажорируемы.
Тогда ![]() – мажоранжа (если ряд сходится), при
– мажоранжа (если ряд сходится), при ![]() .
.
Теорема. О непрерывности суммы ряда
Пусть 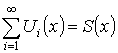 .
.
![]()
![]() – сходится и
– сходится и ![]() ,
, ![]() – непрерывна на
– непрерывна на ![]() .
.
Тогда ![]() – непрерывна на
– непрерывна на ![]() .
.
Доказательство:
![]() (из определения непрерывности)
(из определения непрерывности)
![]() ,
,
где ![]() .
.
При ![]() и
и ![]() .
.
Отсюда ![]()
Пример:
![]() на
на ![]()
![]()
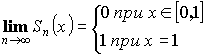 , разрыв при
, разрыв при ![]()
Теорема. О почленном интегрировании ряда
Пусть 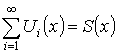 на
на ![]() – мажорируемый,
– мажорируемый, ![]() – интегрируемы на
– интегрируемы на ![]() (
(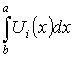 – существует). Тогда
– существует). Тогда 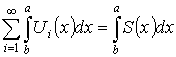
Теорема. О почленном дифференцировании ряда
Пусть 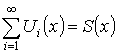 на
на ![]() – мажорируемый,
– мажорируемый, ![]() – дифференцируемы на
– дифференцируемы на ![]() (
(![]() – существует). Тогда
– существует). Тогда 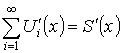
9.2. Степенные ряды
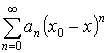 , где
, где ![]() – коэффициент,
– коэффициент, ![]() – произвольная точка,
– произвольная точка, ![]() .
.
Частный случай: 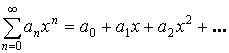
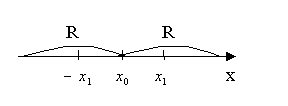
Теорема Абеля: У каждого степенного ряда существует радиус сходимости.
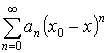 , при
, при
![]() – сходится
– сходится
![]() – расходится.
– расходится.
![]() – точка сходимости.
– точка сходимости.
Если ![]() , то
, то ![]() , т.е.
, т.е. ![]() – мажорируемый.
– мажорируемый.
Область сходимости: ![]()
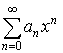 – сходится при
– сходится при ![]()
Пример:
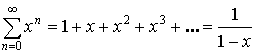 – сходится при
– сходится при ![]() .
.
Теорема. Радиус сходимости ![]() определяется как
определяется как 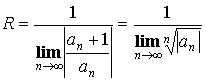 .
.
Доказательство:
Возьмем ![]() , тогда
, тогда 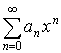
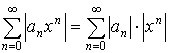
По признаку Даламбера:
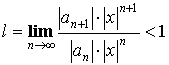
Отсюда 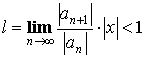 или
или 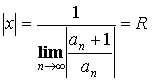
Внутри радиуса сходимости степенной ряд мажорируем, его сумма непрерывна, его можно почленно интегрировать и дифференцировать.
Пример:
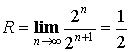 или при
или при ![]() ряд сходится.
ряд сходится.
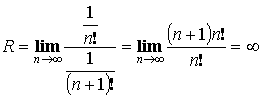 , значит ряд сходится при любых
, значит ряд сходится при любых ![]()
![]() , значит при
, значит при ![]() ряд сходится.
ряд сходится.
Разложение функций в степенной ряд
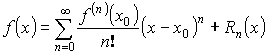 – ряд Тейлора.
– ряд Тейлора.
![]() , тогда
, тогда 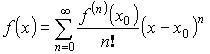
При ![]()
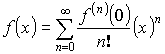 – ряд Маклорена.
– ряд Маклорена.
Разложение некоторых функций в степенной ряд
![]() или
или ![]() – любое.
– любое.
![]() или
или ![]() – любое.
– любое.
![]() или
или ![]() – любое.
– любое.
-
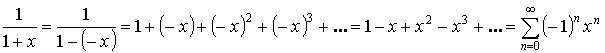
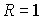 или при
или при 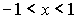 ряд сходится
ряд сходится
![]() или при
или при ![]() ряд сходится
ряд сходится
Сумма знакочередующегося ряда имеет погрешность не превосходящую первого отброшенного члена.
![]()
![]()
Пример:
![]()
Имеем
![]()
![]()
![]()
Получаем
![]()
![]()
Считая, что 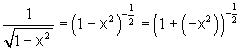
Пример:
![]()
Контрольные примеры:
-
- Разложим в ряд
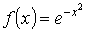 и посчитаем
и посчитаем 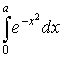
- Разложим в ряд
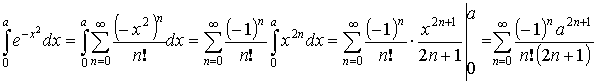
- Разложим в ряд
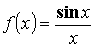 и посчитаем
и посчитаем 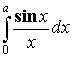
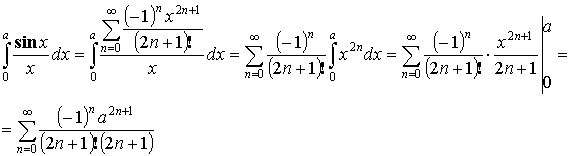
Пример разложения функции в ряд Маклорена:
![]()
![]()
![]()
![]()
![]()
Получаем ![]()