Энтропия дискретного случайного сигнала определяется выражением (2). Для непрерывной случайной величины воспользуемся этим же выражением, заменив вероятность p(x) на w(x)dx.
В результате получим
.
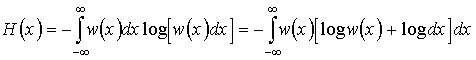Но логарифм бесконечно малой величины (dx) равен минус бесконечности, в результате чего получаем
.
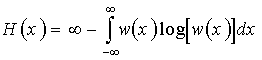Таким образом, энтропия непрерывной случайной величины бесконечно велика. Но так как в последнем выражении первое слагаемое (¥) от величины x или от w(x) не зависит, при определении энтропии непрерывной величины это слагаемое отбрасывают, учитывая только второе слагаемое (некоторую “добавку” к бесконечности). Эта добавочная энтропия, определяемая формулой
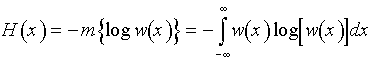(31)
-называется дифференциальной энтропией непрерывной случайной величины.
В дальнейшем слово “дифференциальная” в определении энтропии будем иногда опускать.
Как и для дискретных сообщений, существуют следующие разновидности дифференциальной энтропии непрерывной величины.
1. Условная энтропия случайной величины y относительно случайной величины x.
, или
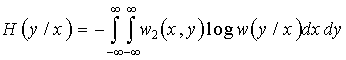. (32)
2. Совместная энтропия двух непрерывных случайных величин равна
, или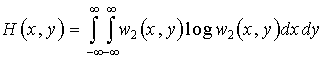 
. (33)
Для независимых x и y H(x,y)=H(x)+H(y).
Для совместной дифференциальной энтропии непрерывной случайной величины справедливы соотношения (17) и (18).
3. Взаимная информация I(x,y), содержащаяся в двух непрерывных сигналах x и y, определяется формулой (16).
Для независимых x и y взаимная информация I(x,y)=0.
4. Если случайная величина ограничена в объёме V=b-a, то её дифференциальная энтропия максимальна при равномерном закона распределения этой величины (рис. 10).
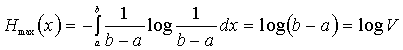. (34)
Так как эта величина зависит только от разности (b-a), а не от абсолютных величин b и a, следовательно, Hmax(x) не зависит от математического ожидания случайной величины x.
5. Если случайная величина не ограничена в объёме (т.е. может изменяться в пределах от -¥ до +¥), а ограничена только по мощности, то дифференциальная энтропия максимальна в случае гауссовского закона распределения этой величины. Определим этот максимум.
В соответствии с (31)
;
.
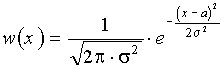Отсюда
.
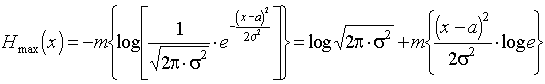Но математическое ожидание m{(x-a2)}=s2, отсюда получаем
,
или окончательно
. (35)
Cледовательно, энтропия зависит только от мощности s2.
Эта очень важная формула будет использоваться позднее для определения пропускной способности непрерывного канала связи.
Заметим, что, как и ранее, Hmax(x) не зависит от математического ожидания a случайной величины x. Это важное свойство энтропии. Оно объясняется тем, что математическое ожидание является не случайной величиной.
Вопросы
- Как определяется дифференциальная энтропия непрерывной случайной величины? Разновидности энтропии непрерывной случайной величины.
- Чему равна максимальная дифференциальная энтропия, если случайная величина ограничена в объёме, при каком законе распределения она максимальна?
- Чему равна максимальная дифференциальная энтропия, если случайная величина не ограничена в объёме?
- Как влияет математическое ожидание случайной величины на её энтропию?