Д.1.1. Стандартное преобразование Лапласа
Д.1.2. Свойства преобразования Лапласа
Д.1.3. Использование преобразования Лапласа
Д.3.1. Передаточная функция цифрового фильтра
Д.3.2. Устойчивость однополюсного фильтра
Д.3.3. Устойчивость произвольного фильтра
Д.3.4. Диаграмма полюсов-нулей и единичная окружность
Д.3.5. Дискретное преобразование Фурье импульсной характеристики цифрового фильтра
Д.4. Фильтры с конечной импульсной характеристикой
Д.4.1. Структура фильтра с конечной импульсной характеристикой
Д.5. Фильтры с бесконечной импульсной характеристикой
Д.1. Преобразование Лапласа
Напомним преобразование Фурье, приведенное в формуле (А.26) приложения А.
или 
, (Д.1)
где 
.
Определим новую функцию v(t), равную x(t), умноженному на 
, где 
- вещественное число, т.е. v(t) = x(t). Фурье-образ функции v(t) будет выглядеть следующим образом.
(Д.2)
Таким образом, можно переписать формулу (Д.1).
(Д.3)
Пусть s - комплексная частота, s =
, тогда Фурье-образ временного сигнала x(t) можно определить следующим образом.
, (Д.4)
где s — переменная Лапласа. Перепишем обратное преобразование Фурье, приведенное в формуле (А.27), через угловую частоту ; тогда 
и
(Д.5)
Поскольку 
, из этого следует, что ds/dw = i, и мы можем определить обратное преобразование Лапласа следующим образом.
(Д.6)
Формулы (Д.4) и (Д.6) представляют пару преобразований Лапласа 
, или, более точно, пару двусторонних преобразований Лапласа. Если (разумно) предположить, что до момента t = 0 сигнал не существует (т.е. является причинным), то преобразование можно назвать односторонним, что записывается следующим образом.
(Д.7)
Обратное одностороннее преобразование Лапласа аналогично преобразованию, приведенному в формуле (Д.6). Таким образом, формулы (Д.6) и (Д.7) можно называть парой односторонних преобразований Лапласа.
Д. 1.1. Стандартное преобразование Лапласа
В табл. Д.1 приведены некоторые стандартные односторонние преобразования Лапласа. Отметим, что (двустороннее) преобразование Лапласа, приведенное в формуле (Д.4), идентично преобразованию Фурье, приведенному в формуле (А.26), при s=iw, где . Для создания преобразования Лапласа x(t) умножается на "множитель сходимости" , где - любое вещественное число. Таким образом, при фактическом вычислении значений интегралов преобразование Лапласа может существовать для многих функций, для которых отсутствует соответствующее преобразование Фурье. Одним из ключевых преимуществ преобразования Лапласа является возможность преобразования функций, не являющихся абсолютно интегрируемыми.
Таблица Д.1. Преобразования Лапласа
|
Тип сигнала |
Временная функция |
Преобразование Лапласа |
| Импульс |
|
|
|
Единичная ступенчатая функция (Хевисайда) |
|
|
| Линейно растущая функция |
|
|
| Экспоненциальные функции |
|
|
| Синусоида |
|
|
| Косинусоида |
|
|
| Затухающая синусоида |
|
|
| Затухающая косинусоида |
|
|
Д.1.2. Свойства преобразования Лапласа
Можно показать, что если известна пара преобразований Лапласа y(t)
Y(s), то для запаздывающей версии сигнала, которая записывается как y(t -t0), справедливо следующее.
(Д.8)
Данное свойство называется свойством смешения во времени. Другие свойства-преобразования Лапласа приведены в табл. Д.2. Их справедливость можно проверить путем простой подстановки в интегральное выражение, описывающее соответствующее преобразование. Отметим, что соотношение 
между преобразованиями Фурье и Лапласа означает, что существует простой эквивалентный переход между преобразованиями, приведенными в табл. Д.1 и А.1, и свойствами, указанными в табл. Д.2 и А.2.
Таблица Д.2. Свойства преобразования Лапласа
|
Свойство |
Временная функция |
Преобразование Лапласа |
|
Произвольная функция |
|
|
|
Произвольная функция |
|
|
|
Линейность |
|
|
|
Сдвиг во времени ( |
|
|
|
Масштабирование времени |
|
|
|
Модуляция |
|
|
|
Дифференцирование |
|
|
|
Интегрирование |
|
|
|
Свертка |
|
|
> 0)
Д.1.3. Использование преобразования Лапласа
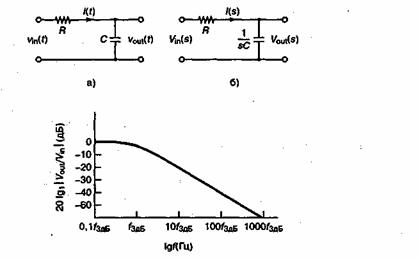
Преобразования Лапласа полезны, когда требуется решать дифференциальные (по времени) уравнения или выполнять операцию свертки. Например, для нахождения тока i(t) простой RС-цепи, показанной на рис. Д.1, отметим, что сумма напряжений на конденсаторе и сопротивлении равна входному напряжению.
(Д.9)
Если входное напряжение — это единичная ступенчатая функция 
, a, q — заряд конденсатора (в кулонах), то, применяя к обеим частям формулы (Д.9) преобразование Лапласа и используя табл. Д.1 и Д.2, получаем следующее.
откуда следует 
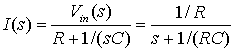(Д.10)
в)
Рис. Д.1. Использование преобразования Лапласа:
а) КС-контур; б) представление с помощью преобразования Лапласа;
в) амплитудная характеристика
(Для единичной ступенчатой функции Vin(s) = 1/s.) Затем, возвращаясь во временную область (и снова используя таблицы свойств преобразования Лапласа), получаем следующее.
(Д.11)
Д.1.4. Передаточная функция
С помощью преобразования Лапласа можно определить (через переменную s) передаточную функцию линейной системы. Из уравнения (Д. 10) при нулевом сопротивлении R= 0 импеданс конденсатора можно вычислить следующим образом.
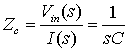(Д.12)
Входное и выходное напряжения (в s-области) можно записать следующим образом.
и 
(Д.13)
Таким образом, (в s-области) передаточную функцию можно определить следующим образом.
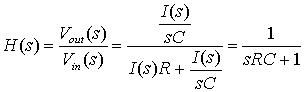(Д.14)
Д.1.5. Фильтрация нижних частот в RC-цепи
Пусть на вход RС-цепи подается комплексная синусоида 
. Используя сказанное выше, можем перейти к преобразованию Фурье, положив s = iw, где . Таким образом, из передаточной функции можно получить частотную характеристику цепи.
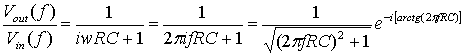(Д.15)
Для малых значений 
; а для больших значений 
. Если 
, то |H(f)|
. Отметим, что 
дБ; следовательно, f0 - это частота по уровню -3дБ, когда выходное напряжение вдвое меньше входного. Следовательно, формула (Д.15) задает тот же фильтр нижних частот, что и формула (1.63). Низкие частоты проходят через фильтр, а высокие — подавляются; данная ситуация показана на рис. Д.1, в.
Д.1.6. Полюсы и нули
Линейные системы, а, следовательно, и (линейные) аналоговые фильтры, можно представить через дифференциальные уравнения во временной области. Рассмотрим, например, следующее уравнение второго порядка.
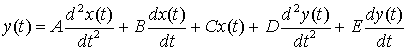(Д.16)
Реализация дифференцирования и/или интегрирования различных порядков происходит с использованием емкостей и индуктивностей вместе с усилителями с обратной связью, имеющими нужный порядок [2]. Применяя преобразование Лапласа к обеим частям уравнения (Д. 16), получаем более удобное (с точки зрения математики и формы записи) уравнение Лапласа.
Y(s) = As2X(s) + BsX(s) + CX(s) + Ds2Y(s) + EsY(s) (Д.17)
Передаточная функция записывается в следующем виде.
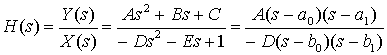(Д.18)
Корни числителя 
называются нулями, а корни знаменателя 
- полюсами. Отметим, что если А, В и С - вещественны, нули являются комплексно-сопряженными.
Д.1.7. Устойчивость линейных систем
Рассмотрим однополюсное уравнение, соответствующее некоторой линейной системе.
(Д.19)
Импульсную характеристику данной системы можно (используя табл. Д.1) найти как обратное преобразование Лапласа выражения (Д.19); если 
, то импульсная характеристика выглядит следующим образом.
(Д.20)
Видим, что Re[] =
; если >0, импульсная характеристика расходится с увеличением t (времени). В то же время, если <0, импульсная характеристика сходится с увеличением t. Член 
— это комплексная (осциллирующая) синусоида (см. раздел А.2.1). Используя формулировку, несколько отличающуюся от применяемых ранее, можно сказать, что система устойчива, если все полюса в s-области имеют отрицательную действительную часть.
Таким образом, если изобразить полюса на комплексной s-плоскости, все они должны располагаться в ее левой части. На рис. Д.2 показана область устойчивости и приведен пример устойчивой передаточной функции третьего порядка, все полюса которой попадают в левую часть комплексной s-плоскости, т.е. имеют отрицательную действительную часть. Отметим, что нули функции могут быть в левой или правой части s-плоскости, и это не влияет на устойчивость.
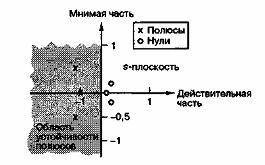
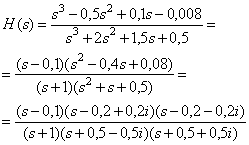
Нули в точках s = 0,1, 0,2-0,2i, 0,2+0,2i
Полюсы в точках s= -1, -0,5-0,5i, -0,5+0,5i
Рис. Д.2. Нули и полюса передаточной функции, изображенные в s-области
Если цепь имеет более одного полюса, передаточную функцию можно рассматривать как последовательность однополюсных функций.
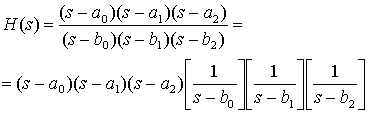(Д.21)
Для устойчивости все полюсы должны находиться в левой части комплексной плоскости. Отметим, что для реальных схем с вещественными коэффициентами Лапласа (т.е. в уравнении (Д. 16) а, В, С, D и Е — вещественные) полюсы и нули будут вещественными или будут разбиты на пары комплексно-сопряженных величин, как показано на рис. Д.2.
Для нашего предыдущего примера RС-цепи передаточная функция в формуле (Д.14) является безусловно устойчивой, поскольку 
— это всегда положительная величина, что, разумеется, является ожидаемым результатом. Неустойчивость в линейных системах возникает только при наличии в них обратной связи (рекурсии), например, при использовании фильтров с инвертирующими или неинвертирующими усилителями.
Д.2. z-преобразование
По сути, z-преобразование — это дискретный эквивалент преобразования Лапласа. Оно делает возможным удобный математический анализ (стационарный анализ и анализ переходных процессов) и манипулирование сигналами и спектрами. Возможно, наиболее распространенным современным применением z-преобразования является описание дискретных систем и анализ их устойчивости.
z-преобразование позволяет вычислять свертку входного сигнала и характеристики дискретной линейной системы в математически удобном виде. Кроме того, могут определяться нули и полюса системы, что позволяет извлекать информацию о динамическом поведении и устойчивости дискретной системы. Следует отметить, что нули и полюса z-преобразования отличаются от нулей и полюсов преобразования Лапласа.
Д.2.1. Вычисление z-преобразования
z-преобразование можно вывести непосредственно из преобразования Лапласа, определенного в формуле (Д.4), рассмотрев для этого сигнал x(t), выборка которого производится каждые T секунд. Таким образом, сигнал будет представлен как функция дискретного времени: x(0), х(Т), х(2Т), ...= {x(kT)}. Дискретные данные представляют множество взвешенных и смещенных дельта-функций, применение к которым преобразования Лапласа дает следующий результат (использовано свойство сдвига во времени).
(Д.22)
Введем параметр z =
и заменим дискретное время kT номером выборки k. В результате получаем следующее.
(Д.23)
Приведем в качестве примера результат применения z-преобразования к единичной ступенчатой функции (Хевисайда).
(Д.24)
Выше при суммировании геометрической прогрессии было использовано предположение |z| < 1 (область сходимости). В табл. Д.З и Д.4 приведены, соответственно, примеры применения z-преобразования к некоторым распространенным функциям и представлены полезные свойства данного преобразования.
Таблица Д.3. z-преобразование некоторых функций
|
Тип сигнала |
Временная функция |
z-преобразование |
| Импульс |
|
|
| Задержанный импульс |
|
|
| Единичная ступенчатая функция (Хевисайда) |
|
|
| Линейно растущая функция |
|
|
| Экспоненциальная функция |
|
|
| Синусоида |
|
|
| Косинусоида |
|
|
Таблица Д.4. Свойства z-преобразования
|
Свойство |
Временная функция |
Преобразование Лапласа |
| Произвольная функция |
|
|
| Произвольная функция |
|
|
| Линейность |
|
|
| Сдвиг во времени |
|
|
| Модуляция |
|
|
| Экспоненциальное масштабирование |
|
|
| Линейное масштабирование |
|
|
| Свертка |
|
|
Д.2.2. Обратное z-преобразование
Переход из z-области во временную область выполняется посредством обратного z-преобразования [2].
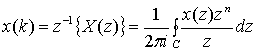(д.25)
Здесь интегрирование в комплексной области 
проводится по любому простому контуру в области сходимости X(z), включающему точку z = 0. Как правило, вычисление обратного z-преобразования сложнее вычисления прямого. Обычно приходится раскладывать подынтегральное выражение на сумму рациональных дробей, делить полиномы, использовать теорему о вычетах и составлять разностные уравнения. Поэтому большая часть z-преобразований и обратных z-преобразований вычисляется с использованием таблиц интегралов и их свойств, так что явного вычисления выражения (Д.25) обычно удается избежать. При современном анализе цифровых сигналов и систем используются программные пакеты, подобные SystemView [1], а z-преобразование большей частью представляет собой просто аналитическую форму записи, удобную для определения устойчивости дискретных сигналов и систем.
Д.З. Цифровая фильтрация
С помощью подходящих аналоговых и цифровых компонентов цифровой фильтр можно настроить на выполнение селекции желаемой частоты или модификации фазы. На рис. Д.З показаны компоненты, необходимые для создания цифрового фильтра, дающего фильтрованную последовательность y(k) при входной последовательности x(k) [2].Выходной сигнал фильтра y(k) создается из взвешенной суммы предыдущих входных сигналов x(k) и предыдущих выходных сигналов y(k-п), где п>0. На рис. Д.4 показан поточный граф сигнала (состоит только из сумматоров, умножителей и схем задержки выборки) для цифрового фильтра с четырьмя весовыми коэффициентами прямой связи и тремя весовыми коэффициентами обратной связи. (Задержка, длительность которой равна длительности одной выборки, обозначена символом 
. Довольно часто подобные графы изображаются с использованием обозначений временной области и z-области, где для представления задержки применяется запись z-1; несмотря на широкое распространение такой формы записи, она не является строгой.)
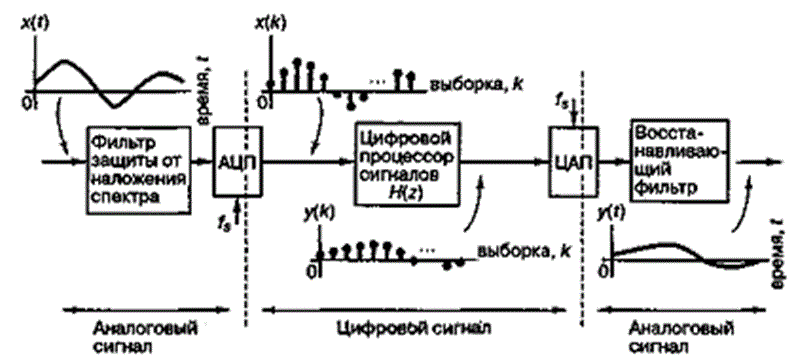
Рис. Д.3. Уравнения цифрового фильтра реализуются на устройстве цифровой обработки сигналов, преобразовывающем входной дискретный информационный сигнал в выходной информационный сигнал
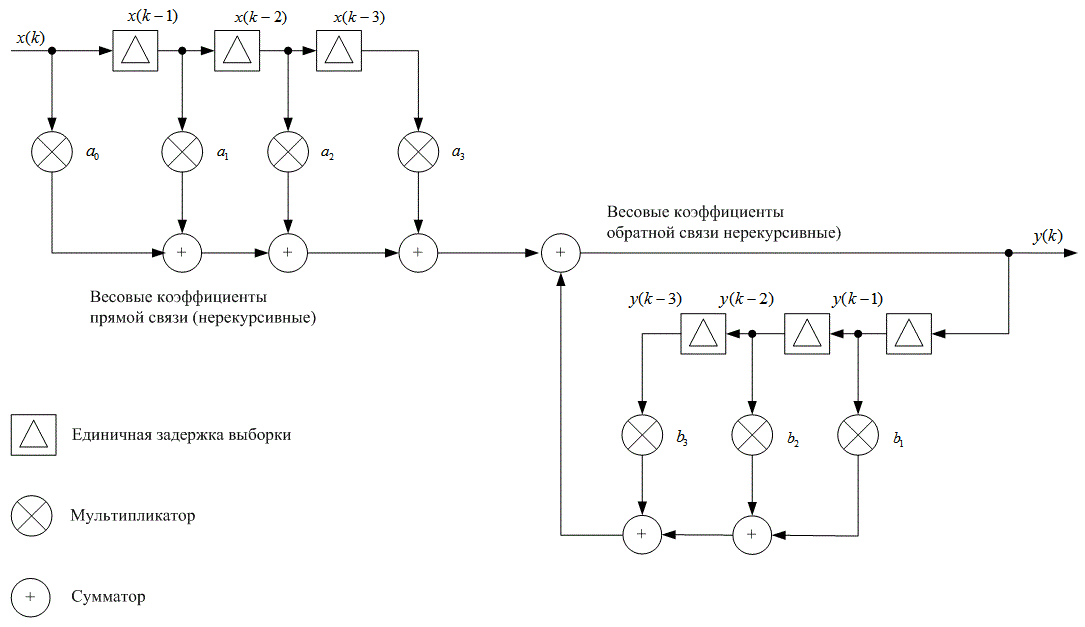
Рис. Д.4. Общая схема цифрового фильтра
Выход данного фильтра описывается следующим выражением.
y(k) = a0x(k) + alx(k-1) + a2x(k-2) + a3x(k-3) + b1у(k -1) + b2у(k - 2) + b3у(k -3) =
=
(Д.26)
Применение z-преобразования к формуле (Д.26) даёт следующий результат.
Y(z)=a0X(z)+alX(z)z-1+a2X(z)z-2+a3X(z)z-3+b1Y(z)z-1+b2Y(z)z-2+b3Y(z)z-3 (Д.27)
Д.3.1. Передаточная функция цифрового фильтра
Передаточная функция цифрового фильтра, изображенного на рис. Д.4, получается после преобразования выражения (Д.27) и выглядит следующим образом.
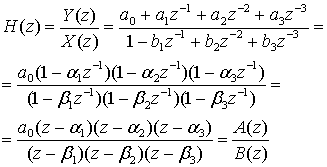(Д.28)
Здесь через 
обозначены нули, а через 
— полюса z-области, которые находятся как корни полинома числителя A(z) и полинома знаменателя B(z). Для цифрового фильтра, подобного изображенному на рис. Д.4, но имеющего N весовых коэффициентов прямой связи и М-1 коэффициентов обратной связи, полиномы числителя и знаменателя в передаточной функции, Приведенной в формуле (Д.28), будут иметь, соответственно, порядок N к М.
Д.3.2. Устойчивость однополюсного фильтра
Вследствие наличия в потоковом графе множественных обратных связей, цифровой фильтр может быть (численно) неустойчивым. Рассмотрим, например, фильтр с одним весовым коэффициентом обратной связи, изображенный на рис. Д.5.
y(k)= x(k) + by(k-1) (Д.29)
Импульсная характеристика данного фильтра (т.е. подача на вход единичного импульса 
плюс применение принципов свертки, описанных в разделе А.5) имеет следующий вид.
h(k) = bk (Д.30)
Если |b|<1, импульсная характеристика фильтра сходится (устойчива); если |b|>1, импульсная характеристика фильтра расходится (неустойчива). На рис. Д.5 показана сходящаяся импульсная характеристика с |b|< 1; более точно, -1<b<1. Применение z-преобразования к выражению (Д. 29) дает следующее.
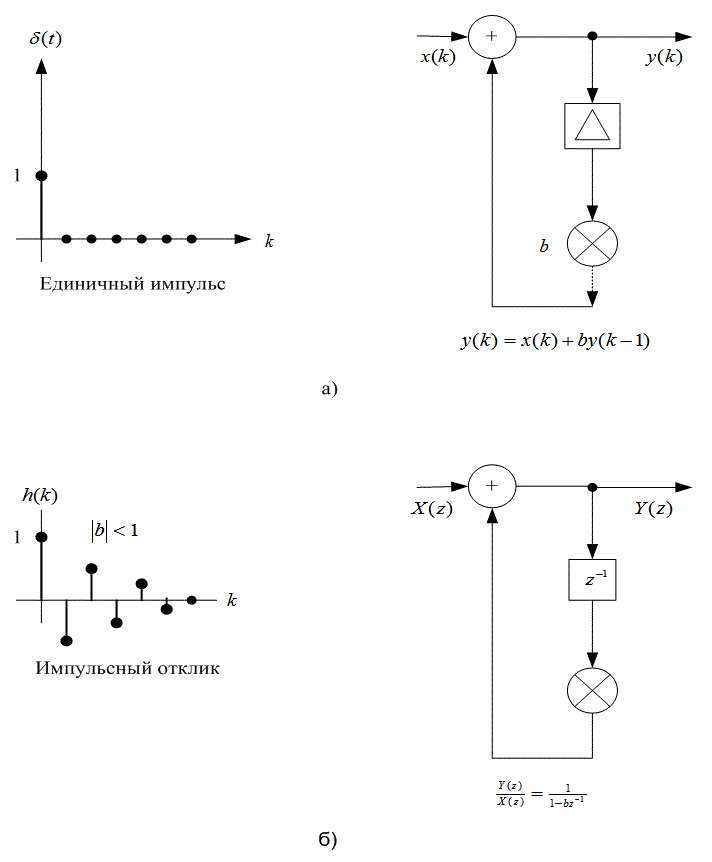
Рис. Д.5. Потоковый граф фильтра с одной обратной связью:
а) во временной области; б) в z-области
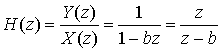(Д.31)
Используя формулу (Д.31), получаем потоковый граф в z-области (рис. Д.5, б), соответствующий потоковому графу во временной области, изображенному на рис. Д.5, а. Элемент задержки (который на рис. Д.5, а обозначен через А) теперь представляется как 
, а вход и выход заданы как z-образы Х(z) и Y(z). Отметим, впрочем, что общая топология двух графов одинакова. (Это частично объясняет то, что потоковые графы цифровых фильтров часто изображаются с использованием обозначений временной области и z-области.) Критерий устойчивости |b|<1) можно сформулировать следующим образом: система устойчива, если полюсы (или корни полинома знаменателя) передаточной функции цифрового фильтра меньше единицы.
Д.3.3. Устойчивость произвольного фильтра
При изучении факторизованной передаточной функции, приведенной в формуле (Д.28), поточный граф, представленный на рис. Д.4 для временной области, можно преобразовать в поточный граф в z-области (рис. Д.6). Последний граф — это, фактически, графическое представление формулы (Д.28), переписанной в следующем виде.
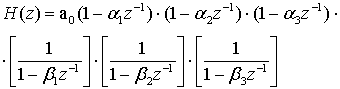(Д.32)
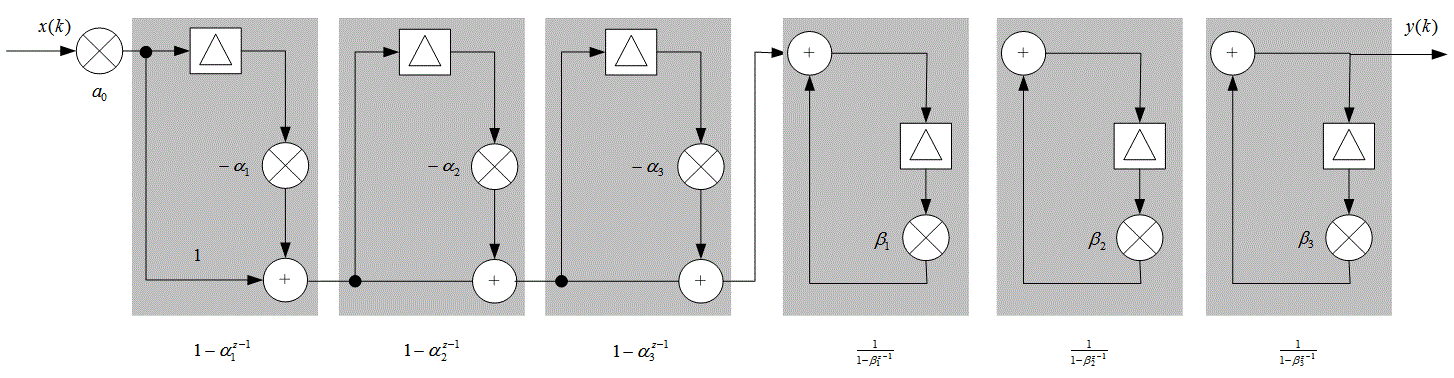
Рис. Д.6. Цифровой фильтр как последовательность каскадов прямой и обратной связи первого порядка
В данном выражении (и на рисунке) обособлены все блоки первого порядка, описываемые нулями и полюсами фильтра. Чтобы фильтр был устойчивым, модули всех полюсов 
каскада должны быть меньше 1. Если хотя бы один блок первого порядка неустойчив (или расходится), неустойчивым является и весь каскад. Как отмечалось для преобразования Лапласа, полюса (и нули) z-области могут быть комплексными, поэтому в качестве критерия устойчивости используется их абсолютная величина, а не амплитуда. (Стоит сказать, что реализация поточного графа, представленная на рис. Д.6, — это всего лишь иллюстрация принципов анализа; реальный цифровой фильтр никогда не реализуется в подобной факторизованной форме, поскольку в этом случае некоторые множители могут быть комплексными, а это может повлечь за собой ненужное усложнение вычислительных требований фильтров.)
Д.3.4. Диаграмма полюсов-нулей и единичная окружность
Если комплексные нули и полюса фильтра или линейной системы изобразить на плоскости с действительной и мнимой осями, данную плоскость можно будет назвать z-плоскостью (или комплексной плоскостью). Система является устойчивой, если все ее полюса находятся внутри единичной окружности. На рис. Д.7 показан вид z-плоскости для следующей передаточной функции.
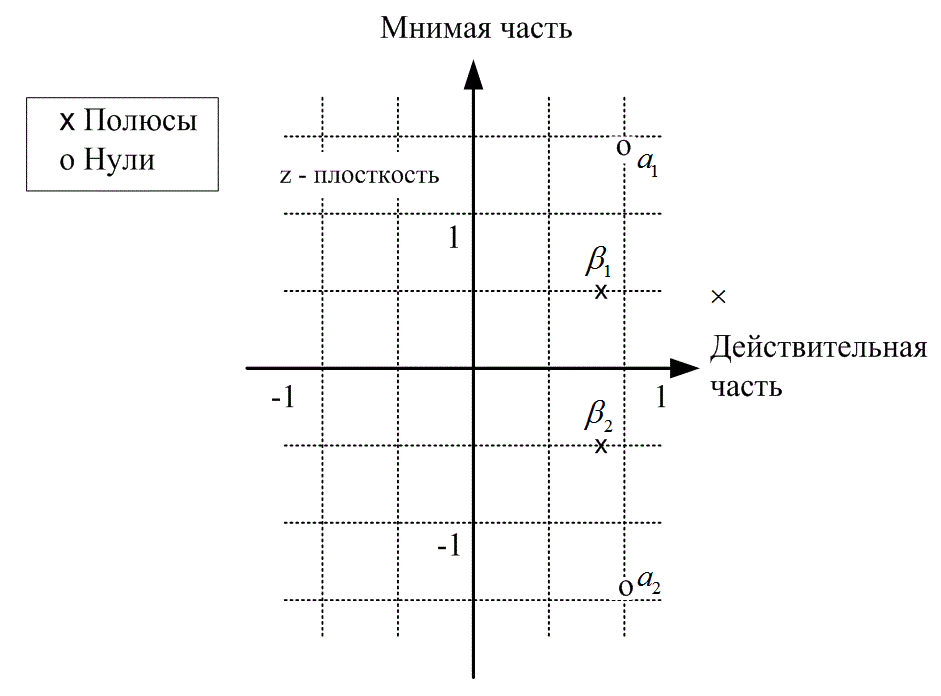
Рис. Д. 7. Полюсы и нули, изображенные на z-плоскости
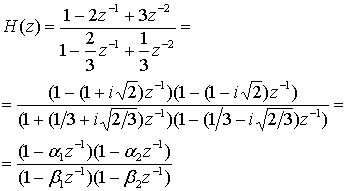(Д.33)
Нули данной функции - 
и 
, полюсы - 
и 
. Поскольку все полюсы лежат внутри единичной окружности, данный фильтр является устойчивым.
Д.3.5. Дискретное преобразование Фурье импульсной характеристики цифрового фильтра
Частотная характеристика цифрового фильтра вычисляется из дискретного преобразования Фурье (discrete Fourier transform — DFT, ДПФ) импульсной характеристики фильтра. Напомним вид преобразования Фурье, приведенного в формуле (А.26).
(Д.34)
Данную формулу можно использовать для вычисления Фурье-образа импульсной характеристики фильтра. Ее можно упростить, полагая, что используется дискретная версия сигнала x(t), причем выборка сигнала производится каждые Тs = 
секунд.
(Д.35)
Разумеется, импульсная характеристика цифрового фильтра является причинной, и первая выборка импульсной характеристики производится в момент k = 0, а последняя — в момент k = N- 1, что в сумме дает N выборок на одно преобразование. Таким образом, для данного конечного числа выборок можно переписать формулу (Д.25), использовав не явное время kTs, а число выборок k.
(Д.36)
Отметим, что значение выражения (Д.36) вычисляется для непрерывной частотной переменной f. В действительности же нам требуется знать это значение для некоторых определенных частот — нулевой частоты (постоянной составляющей) и гармоник "собственной" частоты; всего N дискретных; частот: 0, f0, 2f0 и так до f5, где 
.
для n от 0 до N-1 (Д.37)
Выражение выше можно упростить, использовав только временной индекс k и частотный индекс п. В результате получаем дискретное преобразование Фурье (discrete Fourier transform — DFT, ДПФ).
для n от 0 до N-1 (Д.38)
Поскольку частота дискретизации сигнала x(k) равна fs выборок/с, сигнал включает налагающиеся (или дублирующиеся) компоненты на частотах свыше 
. Следовательно, при вычислении значения выражения (Д.38) достаточно ограничиться частотами до . Отметим, что формула (Д.38) аналогична формуле (Д.23), если положить 
для последовательности длиной N выборок.
Д.4. Фильтры с конечной импульсной характеристикой
На настоящий момент наиболее распространенный тип цифровых фильтров - это фильтры с конечной импульсной характеристикой (КИХ), имеющие, как понятно из названия, импульсную характеристику конечной длительности. Данные фильтры не имеют весовых коэффициентов обратной связи (см. рис. Д.4); следовательно, можно сделать вывод об их безусловной устойчивости. Выход фильтра с конечной импульсной характеристикой, приведенного на рис. Д.8, описывается следующим выражением.
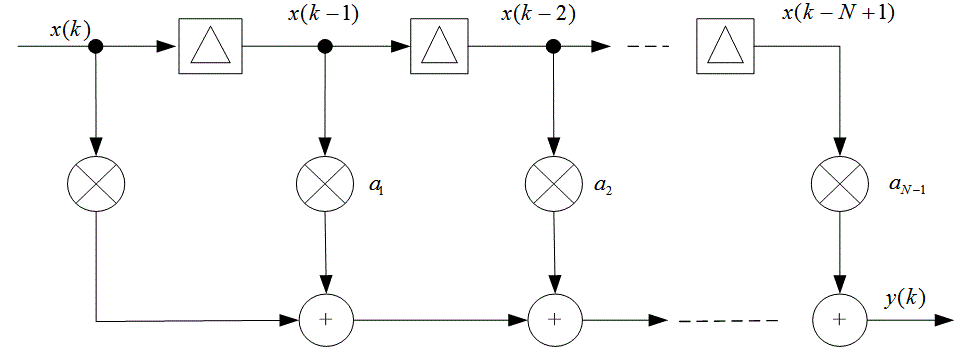
Рис. Д.8. Цифровой фильтр с конечной импульсной характеристикой
(Д.39)
Таким образом, передаточная функция фильтра имеет только нули и не имеет полюсов.
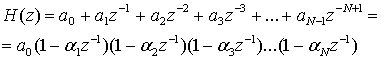(Д.40)
По сути, работа фильтра с конечной импульсной характеристикой — это вычисление текущего среднего; когда выход - это взвешенное среднее N последних входных выборок. Таким образом, фильтры данного типа часто называются фильтрами скользящего среднего (moving average filter). Кроме того, их еще называют линиями задержки с отводами (tapped delay line) и трансверсальными фильтрами (transversal filter).
Д.4.1. Структура фильтра с конечной импульсной характеристикой
В настоящее время цифровые фильтры с конечной импульсной характеристикой разрабатываются с использованием современного программного обеспечения, такого как SystemView [1]. При этом в основе разработки лежит график амплитудной характеристики, на котором указываются допустимые отклонения и пользовательские требования (рис. Д.9). Затем используются классические методы разработки фильтров, такие как метод Паркса-Мак-Леллана (Parks, McLellan), замена Ремеза (Remez Exchange), окно Кайзера и др. [4], в результате чего создается фильтр с подходящей частотной характеристикой, имеющей минимальное число весовых коэффициентов. Если не оговорено противное, большинство фильтров с конечной импульсной характеристикой разрабатывается в расчете на линейное изменение фазы или постоянную групповую задержку (что соответствует симметричной импульсной характеристике).
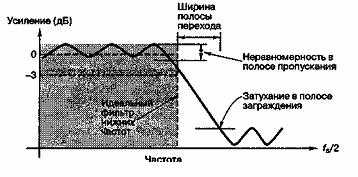
Рис. Д.9. Типичная амплитудная характеристика фильтра нижних частот. Чем строже требования к затуханию в полосе заграждения и полосе перехода и чем ниже допустимая неравномерность в полосе пропускания, тем больше требуется весовых коэффициентов
На рис. Д.10 показаны импульсная и частотная характеристики цифрового фильтра со следующими параметрами: частота среза = 1000Гц, затухание в полосе заграждения = 20дБ, неравномерность в полосе пропускания = 3дБ, полоса перехода = 500Гц, частота дискретизации, fs = 10000Гц. Если нужен фильтр с более строгими требованиями к частотной характеристике (например, нужно более сильное затухание в полосе заграждения), то, скорее всего, на стадии проектирования фильтра с конечной импульсной характеристикой обнаружится, что требуется больше весовых коэффициентов [4].
Д.4.2. Дифференциатор с конечной импульсной характеристикой
Рассмотрим простой цифровой дифференциатор, показанный на рис. Д.11. После изучения выхода для входных синусоид с высокой и низкой частотами, интуитивно можно предположить, что данный дифференциатор — это фильтр верхних частот. Выходная последовательность данного фильтра описывается следующим выражением.
(Д.41)
Применение z-преобразования к обеим частям формулы, (Д.41) приводит к следующему результату.
(Д.42)
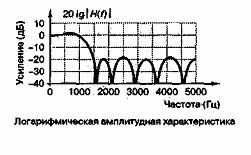
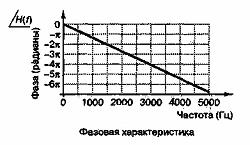
Рис. Д.10. Импульсная характеристика h(n) = wn и частотная харак-теристика Н(f) фильтра нижних частот с 15 весовыми коэффициентами; частота дискретизации = 10 000Гц, частота среза = 1000Гц
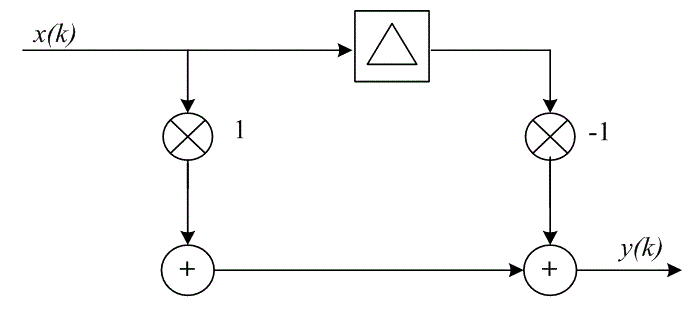
Рис. Д. 11. Дифференциатор/фильтр верхних частот
Следовательно, передаточная функция имеет следующий вид.
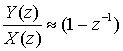(Д.43)
На рис. Д.12 показано, почему данная схема действует как фильтр верхних частот. По сути, выход фильтра — это разность двух последних выборок. Если разность последовательных выборок мала (как для случая низкой частоты), выход будет небольшим. Если разность велика (как для высоких частот), выход будет большим. Если на вход подать сигнал постоянного тока, то выходная амплитуда будет нулевой, т.е. будет происходить бесконечное затухание. Частотную характеристику также можно найти как Фурье-образ импульсной характеристики.
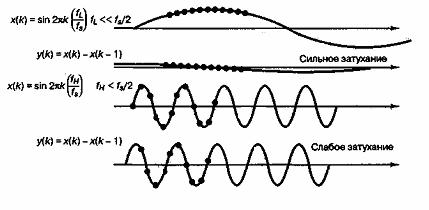
Рис. Д.12. Цифровой дифференциатор, действующий как фильтр верхних частот
Если весовые коэффициенты фильтра изменить с {1, -1} на {1/Т, -1/Т}, где частота дискретизации fs=1/Т, то для входных низкочастотных сигналов выход, у(k), — это приблизительно дифференциал входа.
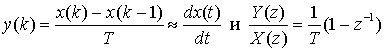(Д.44)
Д.5. Фильтры с бесконечной импульсной характеристикой
Фильтры с бесконечной импульсной характеристикой (infinite impulse response — IIR, БИХ) обычно создаются из аналоговых прототипов с использованием отображения из s-плоскости в z-плоскости. Как понятно из названия, импульсная характеристика таких фильтров (предполагая арифметику бесконечной точности) может иметь бесконечную длительность. Данные фильтры имеют весовые коэффициенты и прямой, и обратной связи, подобно тому, как показано на рис. Д.4. Вследствие рекурсивной природы поточного графа, данные фильтры могут иметь весьма длительные импульсные характеристики (до нескольких весовых коэффициентов). Следовательно, фильтры с бесконечной импульсной характеристикой могут создаваться с меньшим числом весовых коэффициентов, чем фильтры с конечной импульсной характеристикой при аналогичных функциональных амплитудных характеристиках. В общем случае в цифровых фильтрах с бесконечной импульсной характеристикой фаза изменяется нелинейно.
Д.5.1. Оператор левосторонней разности
Уравнение (Д.44) позволяет связать переменную преобразования Лапласа s (непрерывное время) и переменную z-преобразования z (дискретное время). Известно, что при преобразовании Лапласа дифференцирование по времени (d/dt) переходит в умножение на переменную s.
(Д.45)
Возьмем, например, следующую характеристику фильтра Баттерворта.
(Д.46)
Данную аналоговую схему (фильтр нижних частот) можно аппроксимировать дискретно, подставив приближение
(Д.47)
в уравнение (Д.46). Это дает следующее уравнение в z-области.
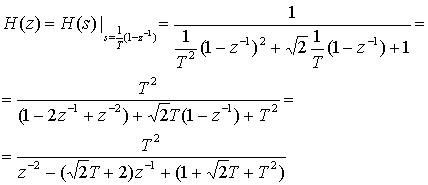(Д.48)
При низких частотах, когда приближение (Д.47) является "хорошим", данное преобразование может давать "разумный" цифровой эквивалент аналогового фильтра нижних частот. (Уравнение (Д.47) иногда называется "оператором левосторонней разности".) К сожалению, данное отображение является очень плохим при высоких частотах, а, следовательно, оно не может использоваться при создании фильтров верхних частот. Таким образом, на практике оно применяется редко.
Д.5.2. Использование билинейного преобразования для создания фильтров с бесконечной импульсной характеристикой
Билинейное преобразование получается при замене s следующим приближением.
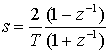(Д.49)
Данная подстановка приводит к отображению, сохраняющему устойчивость аналогового прототипа и дающему фильтры, значительно лучшие по своим характеристикам, чем в предыдущем случае (уравнение (Д.47)) [2]. В SystemView [1] билинейное преобразование используется для создания цифровых фильтров из стандартных аналоговых прототипов, таких как фильтры Баттерворта, эллиптические фильтры и фильтры Чебышева. Отметим, что билинейное преобразование всегда дает фильтр, имеющий нули и полюсы; следовательно, данные фильтры имеют бесконечную импульсную характеристику (БИХ).
Д.5.3. Интегратор с бесконечной импульсной характеристикой
Цифровой интегратор — это, по сути, БИХ-фильтр с одним весовым коэффициентом.
(Д.50) 
В z-области передаточная функция дискретного интегратора получается из соотношения
Y(z) = X(z) + z-1Y(z), (Д.51)
которое дает следующее.
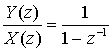(Д.52)
Реализация простого цифрового интегратора и графическое представление связи с интегрированием по непрерывному времени показаны на рис. Д.13.
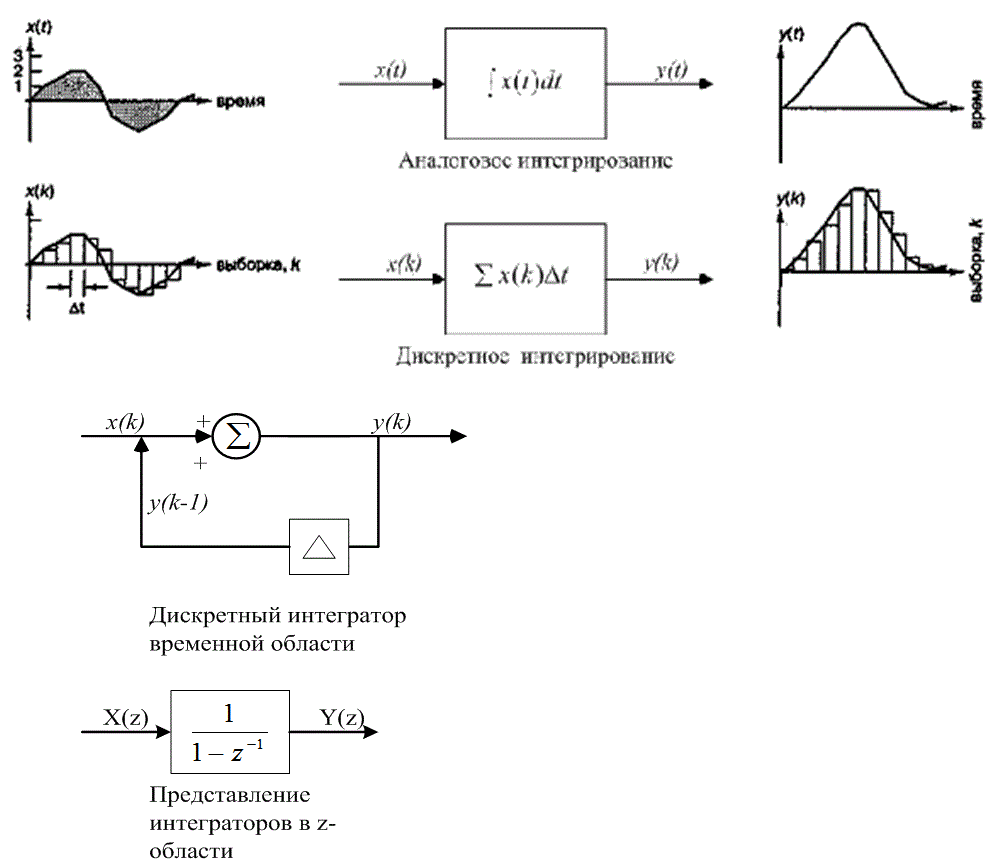
Рис. Д. 13. Однополюсный фильтр, действующий как интегратор. В контур обратной связи часто вводится весовой коэффициент, немного меньший 1, который обеспечивает "забывание " интегратора
Если в контур обратной связи вводится весовой коэффициент, меньший 1 (скажем, 0,99), интегратор часто называют квазиинтегратором (leaky integrator). При рассмотрении в частотной области, характеристики (квази) интегратора и фильтра нижних частот не отличаются.
Литература
1. SystemViev DSP Communications Software. Elanix, Westlake Village, CA, 2000.
2. Porat. B. A Course in Digital Signal Processing. John Wiley & Cons, 1997.
3. Moon T. K., Stirling W. C. Mathematical Methods and Algorithms for Digital Signal Processing. Prentice Hall, 2000.
4. Stewart R. W. The DSPedia: A Multimedia Resource for DSP. BlueBox Multimedia, UK, 2000.