4.9.1. Вероятность символьной ошибки для модуляции MPSK
4.9.1. Вероятность символьной ошибки для модуляции MPSK
Для больших отношений сигнал/шум вероятность символьной ошибки ![]() для равновероятных сигналов в M-арной модуляции PSK с когерентным обнаружением можно выразить как [7]
для равновероятных сигналов в M-арной модуляции PSK с когерентным обнаружением можно выразить как [7]
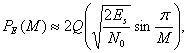 (4.105)
(4.105)
где ![]() — вероятность символьной ошибки,
— вероятность символьной ошибки, ![]() — энергия, приходящаяся на символ, а М = 2k — размер множества символов. Зависимость
— энергия, приходящаяся на символ, а М = 2k — размер множества символов. Зависимость ![]() от
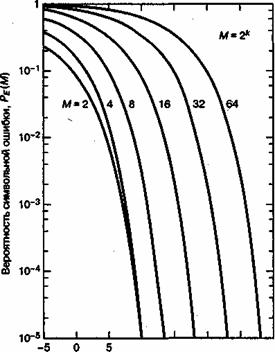
от ![]() для передачи сигналов MPSK с когерентным обнаружением показана на рис. 4.35.
для передачи сигналов MPSK с когерентным обнаружением показана на рис. 4.35.
![]()
Рис. 4.35. Вероятность символьной ошибки для многофазной передачи сигналов с когерентным обнаружением. (Перепечатано с разрешения авторов из W. С. Lindsey and M. К. Simon. Telecommunication Systems Engineering. Prentice-Hall, Inc., Engle-wood Cliffs, N. J., 1973.)
Вероятность символьной ошибки для дифференциального когерентного обнаружения М-арной схемы DPSK (для больших значений ![]() ) выражается подобно тому, как это было приведено выше [7].
) выражается подобно тому, как это было приведено выше [7].
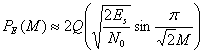 (4.106)
(4.106)
4.9.2. Вероятность символьной ошибки для модуляции MFSK
Вероятность символьной ошибки ![]() для равновероятных ортогональных сигналов с когерентным обнаружением можно выразить как [5]
для равновероятных ортогональных сигналов с когерентным обнаружением можно выразить как [5]
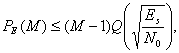 (4.107)
(4.107)
где ![]() — энергия, приходящаяся на символ, а M — размер множества символов. Зависимость
— энергия, приходящаяся на символ, а M — размер множества символов. Зависимость ![]() от
от ![]() для М-арных ортогональных сигналов с когерентным обнаружением показана на рис. 4.36.
для М-арных ортогональных сигналов с когерентным обнаружением показана на рис. 4.36.
Вероятность символьной ошибки для равновероятных М-арных ортогональных сигналов с некогерентным обнаружением дается следующим выражением [9].
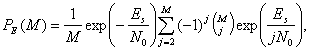 (4.108)
(4.108)
где
![]() (4.109)
(4.109)
является стандартным биномиальным коэффициентом, выражающим число способов выбора j ошибочных символов из М возможных. Отметим, что для бинарного случая формула (4. 108) сокращается до
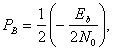 (4.110)
(4.110)
что совпадает с результатом, полученным в выражении (4.96). Кривая зависимости ![]() от
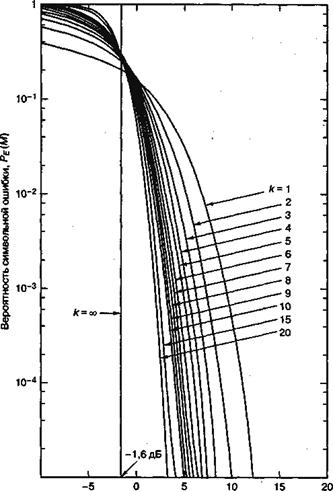
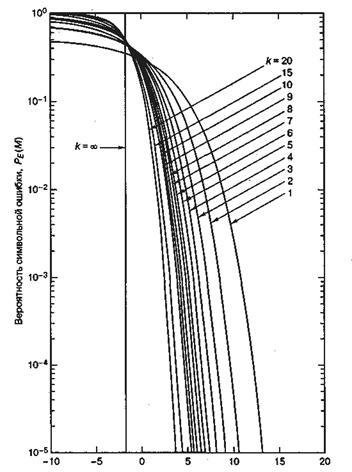
от ![]() для M-арной передачи сигналов с некогерентным обнаружением изображена на рис. 4.37. При сравнении данных графиков с приведенными на рис. 4.6 и соответствующими когерентному обнаружению можно заметить, что для k > 7 различием уже можно пренебрегать. В заключение отметим, что для когерентного и некогерентного приема ортогональных сигналов верхний предел вероятности ошибки дается выражением [9].
для M-арной передачи сигналов с некогерентным обнаружением изображена на рис. 4.37. При сравнении данных графиков с приведенными на рис. 4.6 и соответствующими когерентному обнаружению можно заметить, что для k > 7 различием уже можно пренебрегать. В заключение отметим, что для когерентного и некогерентного приема ортогональных сигналов верхний предел вероятности ошибки дается выражением [9].
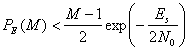 (4.111)
(4.111)
Здесь Es — энергия на символ, а М — размер алфавита символов.
![]()
Рис. 4.36. Вероятность символьной ошибки для М-арной ортогональной передачи сигналов с когерентным обнаружением. (Перепечатано с разрешения авторов из W. С. Lindsey and M. К. Simon. Telecommunication Systems Engineering. Prentice-Hall, Inc., Englewood Cliffs, N. J., 1973.)
4.9.3. Зависимость вероятности битовой ошибки от вероятности символьной ошибки для ортогональных сигналов
Можно показать [9], что соотношение между вероятностью битовой ошибки (РВ) и вероятностью символьной ошибки (РЕ) для ортогональных M-арных сигналов дается следующим выражением.
![]() (4.112)
(4.112)
![]()
Рис. 4.37. Вероятность символьной ошибки для М-арной ортогональной передачи сигналов с некогерентным обнаружением. (Перепечатано с разрешения авторов из W. С. Lindsey and М. К. Simon, Telecommunication Systems Engineering. Prentice-Hall, Inc., Engtewood Cliffs, N. J., 1973.)
В пределе при увеличении k получаем следующее.
![]()
![]()
Понять формулу (4.112) позволяет простой пример. На рис. 4.38 показан восьмеричный набор символов сообщения. Эти символы (предполагаемые равновероятными) передаются с помощью ортогональных сигналов, таких как сигналы FSK. При использовании ортогональной передачи ошибка принятия решения равновероятно преобразует верный сигнал в один из (М - 1) неверных. Пример на рисунке демонстрирует передачу символа, состоящего из битов 011. Ошибка с равной вероятностью может перевести данный символ в любой из оставшихся 2k- 1 = 7 символов. Отметим, что наличие ошибки еще не означает, что все биты символа являются ошибочными. Если (рис. 4.38) приемник решит, что переданным символом является нижний из указанных, состоящий из битов 111, два из трех переданных битов будут верными. Должно быть очевидно, что для недвоичной передачи РВвсегда будет меньше РЕ (РB и РЕ — средние частоты появления ошибок).
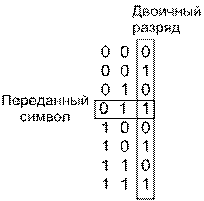
Рис. 4.38. Пример зависимости рв от ре
Рассмотрим любой из столбцов битов на рис. 4.38. Каждая битовая позиция на 50% заполнена нулями и на 50% — единицами. Рассмотрим первый бит переданного символа (правый столбец). Сколько существует возможностей появления ошибочного бита 1? Всего существует 2k- 1 =4 возможности (нули в столбце появляются в четырех местах) появления битовой ошибки; то же значение получаем для каждого столбца. Окончательное соотношение рв/ре Для ортогональной передачи сигналов в формуле (4.112) получается следующим образом: число возможностей появления битовой ошибки (2k-1) делится на число возможностей появления символьной ошибки (2k- 1). Для случая, изображенного на рис. 4.38, ![]() .
.
4.9.4. Зависимость вероятности битовой ошибки от вероятности символьной ошибки для многофазных сигналов
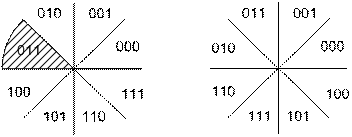
При передаче сигналов MPSK значение РВменьше или равно РЕ, так же как и при передаче сигналов MFSK. В то же время имеется и существенное отличие. Для ортогональной передачи сигналов выбор одного из (М- 1) ошибочных символов равновероятен. При передаче в модуляции MPSK каждый сигнальный вектор не является равноудаленным от всех остальных. На рис. 4.39, а показано восьмеричное пространство решений, где области решений обозначены 8-ричными символами в двоичной записи. При передаче символа (011) и появлении в нем ошибки наиболее вероятными являются ближайшие соседние символы, (010) и (100). Вероятность превращения символа (011) вследствие ошибки в символ (111) относительно мала. Если биты распределяются по символам согласно двоичной последовательности, показанной на рис. 4.39, а, то некоторые символьные ошибки всегда будут давать две (или более) битовые ошибки, даже при значительном отношении сигнал/шум.
а) б)
Рис. 4.39. Области решения в сигнальном пространстве MPSK: а) в бинарной кодировке; 6) в кодировке Грея
Для неортогональных схем, таких как MPSK, часто используется код преобразования бинарных символов в M-арные, такие, что двоичные последовательности, соответствующие соседним символам (сдвигам фаз), отличаются единственной битовой позицией; таким образом, при появлении ошибки в М-арном символе высока вероятность того, что ошибочным является только один из k прибывших битов. Кодом, обеспечивающим подобное свойство, является код Грея (Gray code) [7]; на рис/4.39, б для восьмеричной схемы PSK показано распределение битов по символам с использованием кода Грея. Можно видеть, что соседние символы отличаются одним двоичным разрядом. Следовательно, вероятность появления многобитовой ошибки при данной символьной ошибке значительно меньше по сравнению с некодированным распределением битов, показанным на рис. 4.39, а. Реализация подобного кода Грея представляет один из редких случаев в цифровой связи, когда определенная выгода может быть получена без сопутствующих недостатков. Код Грея — это просто присвоение, не требующее специальных или дополнительных схем. Можно показать [5], что при использовании кода Грея вероятность ошибки будет следующей.
![]() (4.113)
(4.113)
Напомним из раздела 4.8.4, что передача сигналов BPSK и QPSK имеет одинаковую вероятность битовой ошибки. Формула (4.113) доказывает, что вероятности символьных ошибок этих схем отличаются. Для модуляции BPSK РЕ = РВ, а для QPSK РЕ ![]() 2РВ. Точное аналитическое выражение вероятности битовой ошибки РB в восьмеричной схеме PSK, а также довольно точные аппроксимации верхнего и нижнего пределов РB для M-арной PSK при больших М можно найти в работе [10].
2РВ. Точное аналитическое выражение вероятности битовой ошибки РB в восьмеричной схеме PSK, а также довольно точные аппроксимации верхнего и нижнего пределов РB для M-арной PSK при больших М можно найти в работе [10].
4.9.5. Влияние межсимвольной интерференции
Обнаружение сигналов рассматривалось при наличии шума AWGN в предположении, что межсимвольная интерференция (intersymbol interference — ISI) отсутствует. Это упростило анализ, поскольку процесс AWGN с нулевым средним описывается единственным параметром — дисперсией. На практике обычно оказывается, что межсимвольная интерференция — это второй (после теплового шума) источник помех, которому необходимо уделять пристальное внимание. ISI может возникать вследствие использования узкополосных фильтров на выходе передатчика, в канале или на входе приемника. Результатом этой дополнительной интерференции является ухудшение достоверности передачи как для когерентного, так и некогерентного приема. Вычисление вероятности ошибки при ISI (помимо AWGN) является значительно более сложной задачей, поскольку в вычислениях будет фигурировать импульсная характеристика канала. Этот вопрос мы не рассматриваем; впрочем, для читателей, интересующихся данной темой, можно порекомендовать работы [11-16].

