Ранее рассматривались переходные процессы в RL- и RС-цепях, которые относятся к цепям первого порядка, так как описываются дифференциальными уравнениями первого порядка (6.11), (6.23). При наличии в цепи двух независимых накопителей энергии переходные процессы в них описываются уравнением второго порядка. Простейшим примером такой цепи является последовательный колебательный контур (рис. 6.11).

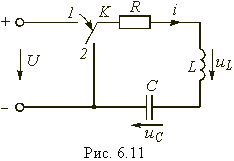
Для этого контура можно по аналогии с RL- и RС-цепью составить дифференциальное уравнение второго порядка, выбрав в качестве независимой переменной напряжение на емкости

Учитывая, что i = Cdu_C/dt окончательно получаем (6.37)

Решение дифференциального уравнения (6.37) ищется согласно (6.5) в форме суммы свободной u_Cсв и принужденной u_Cпр составляющих: (6.38)

Вид u_Cпр зависит от характера приложенного напряжения, а u_Cсв определится решением однородного дифференциального уравнения второго порядка: 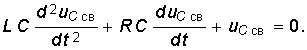(6.39)

Решение уравнения (6.39) зависит от вида корней характеристического уравнения (6.40)

Корни уравнения (6.40) определяются только параметрами цепи независимо от выбранной переменной: 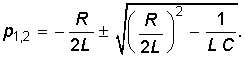(6.41)

Величина a = R/2L носит название коэффициента затухания контура, а есть резонансная частота контура (см. § 4.2). Таким образом, уравнение (6.41) можно переписать в виде (6.42)

Характер переходного процесса существенным образом зависит от вида корней р₁, р₂, которые могут быть: 1) вещественными и различными (при R > 2); 2) комплексно-сопряженными (при R < 2); 3) вещественными и равными (при R = 2).

Здесь = — характеристическое сопротивление контура (см. формулу (4.22)).

Разряд емкости на RL-цепь

Для исследования характера переходного процесса во всех этих случаях рассмотрим разряд емкости С на цепь RL (см. рис. 6.11). Так как до коммутации емкость С была заряжена до напряжения U, то имеем ненулевые начальные условия:

После коммутации (переключение ключа К из положения 1 в положение 2 емкость начнет разряжаться и в цепи возникнет свободный переходный процесс. Найдем закон изменения тока и напряжений на отдельных элементах цепи для случая 1)—3).

В первом случае, когда R > 2, корни p₁ и р₂ в (6.41) будут вещественными и различными, и решение уравнения определится согласно (6.7): (6.43) где A₁ и A₂ — постоянные интегрирования. Для определения A₁ и A₂ запишем еще уравнение для тока в цепи: (6.44)

Постоянные A₁ и A₂ можно найти из начальных условий для u_C(0_–) = U и i(0_–) = 0 (при t = 0_–) и законов коммутации (6.1), (6.2): (6.45)

Из решения системы уравнение (6.45)

В результате получаем уравнения для напряжения U_C и тока i: 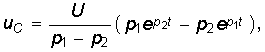(6.46) 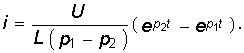(6.47)

Закон изменения напряжения на индуктивности определяется при этом уравнением 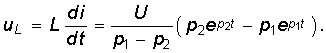(6.48)

Из уравнений (6.46)—(6.48) следует, что каждая из найденных величин u_C, i, u_L состоит из двух слагаемых, затухающих по экспоненте с коэффициентами p₁ < 0 и p₂ < 0. На рис. 6.12 показан характер зависимостей (6.46)—(6.48). Момент времени t₁, соответствующий точке перегиба u_C, максимуму | i | и нулевому значению u_L определяется из решения уравнения di / dt = 0, а момент t₂ из решения уравнения du_L / dt = 0: 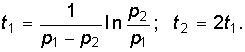(6.49)

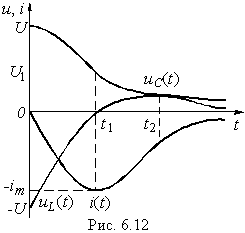
Анализ полученных кривых показывает, что в рассматриваемом случае происходит апериодический разряд емкости С, причем в интервале от 0 до t₁ энергия W_C расходуется на покрытие тепловых потерь в резистивном сопротивлении R и создание магнитного поля в индуктивности ( p_C = u_C i < 0; p_L = u_L i > 0). В дальнейшем (при t > t₁) как энергия электрического поля емкости W_C, так и запасенная к моменту t = t₁ магнитная энергия индуктивности W_L расходуется на покрытие тепловых потерь в сопротивлении R. Отрицательное значение тока свидетельствует о противоположном направлении тока разряда относительно опорного направления.

Во втором случае при R < 2, когда корни p₁ и p₂ носят комплексно-сопряженный характер, (6.50) где называют частотой собственных затухающих колебаний. Решение уравнения (6.39) имеет вид (6.9) (6.51) где A и — постоянные интегрирования. Закон изменения тока в цепи (6.52)

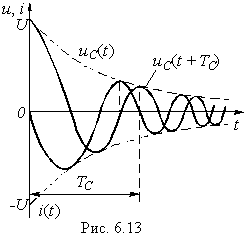
Постоянные A и определяются из начальных условий для u_C и i и законов коммутации (6.1), (6.2): 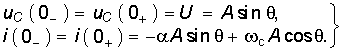(6.53)

Отсюда

Окончательно уравнения для u_C, i и и принимают вид (6.54) 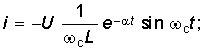(6.55) 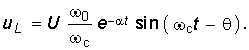(6.56)

Полученные уравнения показывают, что в данном случае имеет место колебательный разряд емкости с частотой _с, зависящей только от параметров R, L, С цепи. Интервал времени Т_c = 2/_с носит название квазипериода. На рис. 6.13 изображены графики зависимостей u_C(t) и i(t) определяемых уравнениями (6.54) и (6.55). Скорость затухания периодического процесса принято характеризовать декрементом затухания, который определяют как отношение двух соседних амплитуд тока или напряжения одного знака (см. рис. 6.13): 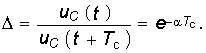(6.57)

На практике чаще используется логарифмический декремент затухания 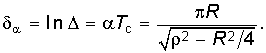(6.58)

Из уравнений (6.57) и (6.58) следует, что затухание тем больше, чем больше R. При R = 2 колебания прекращаются и переходной процесс становится апериодическим. При R = 0 оказываются незатухающие гармонические колебания с частотой _с = ₀ = . Очевидно, что этот случай представляет чисто теоретический интерес, так как в любом реальном контуре имеются потери. В процессе колебательного разряда емкости (свободных колебаний в RLC-контуре) имеет место попеременное запасание энергии W_C в электрическом поле емкости и магнитном поле индуктивности W_L: в начале энергия W_C расходуется на создание магнитного поля W_L индуктивности и покрытие тепловых потерь сопротивления R, затем запасенная энергия W_L, расходуется на перезаряд емкости и покрытие потерь в R и т. д. до полного перехода первоначальной энергии W_c(0) в тепловые потери в резисторе R.

Третий случай R = 2 является пограничным между колебательным и апериодическим и соответствует критическому разряду емкости. Решение уравнения (6.39) при этом имеет вид (6.8) (6.59)

Ток определяется уравнением (6.60) где p₁ = p₂ = p = -a — корни характеристического уравнения (6.40); А₁, А₂ — постоянные интегрирования, определяемые из начальных условий для u_C и i и законов коммутации (6.1), (6.2):

Отсюда А₂ = aU. Окончательные выражения для напряжения и тока принимают вид (6.61) (6.62) (6.63)

По своей форме графики зависимостей (6.61)—(6.63) аналогичны кривым, изображенным на рис. 6.12 с той лишь разницей, что их скорость изменения больше, чем при R > 2. Значение R = 2 носит название критического сопротивления контура.