Комплексная спектральная плотность ![]() непрерывного сигнала
непрерывного сигнала ![]() (в дальнейшем для краткости будем говорить: спектр сигнала) вычисляется по формуле прямого преобразования Фурье
(в дальнейшем для краткости будем говорить: спектр сигнала) вычисляется по формуле прямого преобразования Фурье
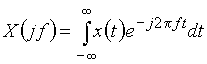 . (3)
. (3)
Сигнал ![]() может быть восстановлен по спектру
может быть восстановлен по спектру ![]() с помощью обратного преобразования Фурье, или интеграла Фурье
с помощью обратного преобразования Фурье, или интеграла Фурье
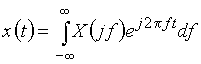 . (4)
. (4)
В соответствии с принципом неопределенности сигнал, имеющий ограниченную протяженность во времени, обладает неограниченным по полосе спектром (рис. 9, а). И наоборот, сигнал с ограниченным спектром имеет бесконечную протяженность во времени (рис. 10, а). Как следует из этих рисунков, непрерывный сигнал, и ограниченной и бесконечной протяженности во времени, имеет сплошной спектр.
Если сигнал ![]() является периодическим, то спектр его – дискретный, т.е. теперь вместо
является периодическим, то спектр его – дискретный, т.е. теперь вместо ![]() используют отсчеты
используют отсчеты ![]() . Эта ситуация показана на рис. 9, б. Период сигнала равен длительности сигнала
. Эта ситуация показана на рис. 9, б. Период сигнала равен длительности сигнала ![]() . Интервал дискретизации спектра по частоте F определяется, как известно, периодом сигнала, в данном случае
. Интервал дискретизации спектра по частоте F определяется, как известно, периодом сигнала, в данном случае ![]() . Формулы для прямого и обратного преобразований Фурье получаются из (3) и (4) путем замены непрерывной частоты f на дискретные значения nF. При этом следует учесть известную связь между амплитудами гармоник
. Формулы для прямого и обратного преобразований Фурье получаются из (3) и (4) путем замены непрерывной частоты f на дискретные значения nF. При этом следует учесть известную связь между амплитудами гармоник ![]() периодического сигнала и отсчетами
периодического сигнала и отсчетами ![]() спектральной плотности
спектральной плотности ![]() непрерывного сигнала:
непрерывного сигнала:
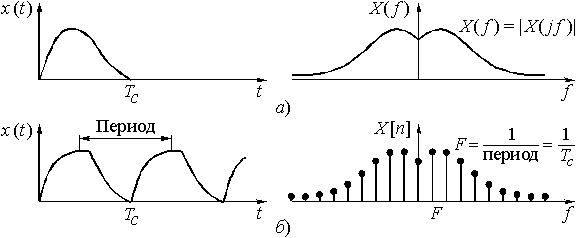
Рис. 9
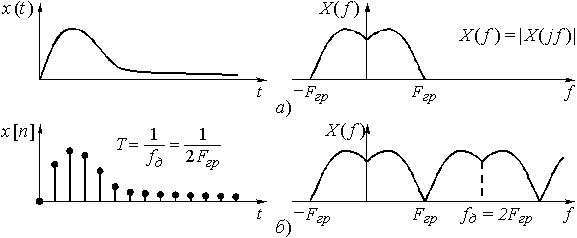
Рис. 10
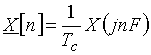 .
.
Спектр ![]() периодического сигнала вычисляется по формуле
периодического сигнала вычисляется по формуле
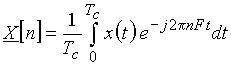 . (5)
. (5)
Сигнал ![]() можно восстановить по его дискретному спектру, воспользовавшись формулой
можно восстановить по его дискретному спектру, воспользовавшись формулой
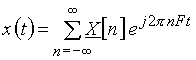 . (6)
. (6)
В соответствии с принципом дуальности можно сказать: если периодическим является спектр, то дискретным будет сигнал (рис. 10, б). Обозначая период повторения спектра ![]() , получим интервал дискретизации сигнала
, получим интервал дискретизации сигнала ![]() .
.
Формулы прямого и обратного преобразований Фурье для дискретных сигналов имеют вид
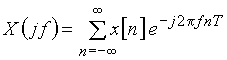 ; (7)
; (7)
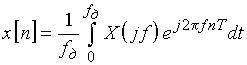 . (8)
. (8)
В формулах (7) и (8) использовано обозначение ![]() .
.
Пример 4.1. Рассчитаем спектр дискретного сигнала, состоящего из одного отсчета ![]() .
.
Воспользуемся формулой (7), в которую подставим значения ![]() заданного сигнала
заданного сигнала
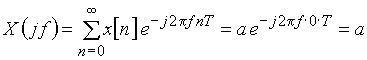 .
.
Пример 4.2. Рассчитаем спектр экспоненциальной дискретной функции ![]() , n³ 0.
, n³ 0.
График дискретной функции ![]() приведен на рис. 11, а ее отсчеты можно записать в виде последовательности
приведен на рис. 11, а ее отсчеты можно записать в виде последовательности ![]() {1; 0,5; 0,25; 0,125; 0,0625; ...}.
{1; 0,5; 0,25; 0,125; 0,0625; ...}.
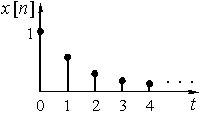
Рис. 11
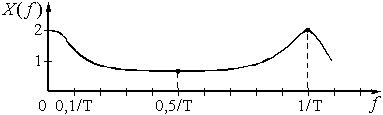
Рис. 12
Спектр дискретной экспоненты рассчитаем по формуле (7)
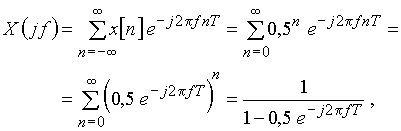
где для суммирования ряда использована формула
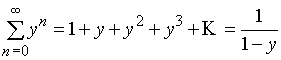 .
.
Получим выражение для расчета спектра амплитуд ![]() , используя формулу Эйлера
, используя формулу Эйлера ![]() .
.
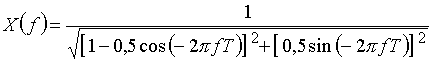 .
.
Для построения графика будем задавать значения f от 0 до 1/Т с шагом 0,1/T и рассчитывать ![]() .
.
График спектра амплитуд ![]() экспоненциальной дискретной функции
экспоненциальной дискретной функции ![]() приведен на рисунке 12.
приведен на рисунке 12.
Как видно из графика, спектр дискретного сигнала сплошной и периодический с периодом ![]() .
.
Самоконтроль
1. Как рассчитывается спектр непериодического (и периодического) непрерывного сигнала?
2. Как восстановить непрерывный сигнал по его спектру (сплошному и дискретному)?
3. Сформулируйте принцип неопределенности.
4. Как рассчитывается спектр дискретного сигнала?
5. Какой спектр у дискретного сигнала: сплошной или дискретный, периодический или непериодический?
6. Как рассчитывается дискретный сигнал, если известен его спектр?
7. Найдите спектр дискретного сигнала, состоящего из одного отсчета ![]() .
.
8. Найдите значения спектра дискретного сигнала, заданного двумя отсчетами ![]() , на частотах
, на частотах ![]() и
и ![]() .
.

