Представление непрерывного сигнала в виде последовательности дискретных отсчётов предполагает, что любой отсчёт может принимать любое значение из непрерывного множества значений . Вместе с тем, цифровые технологии в радиотехнике требуют преобразований совокупности значений отсчётов в цифровую последовательность, т.е. в последовательность чисел. Процесс преобразования аналогового (непрерывного) сигнала в такую последовательность называется аналогово-цифровым преобразованием (АЦП).

Итак, на первом этапе аналогово-цифрового преобразования осуществляется дискретизация непрерывного сигнала, т.е. преобразование в в соответствии с теоремой Котельникова, которая была рассмотрена выше. В результате дискретизации непрерывный (аналоговый) сигнал преобразуется в последовательность отсчётов .

На втором этапе последовательность отсчётов подвергается процедуре квантования по уровню. Квантование по уровню значений отсчётов в простейшем случае представляет собой округление этих значений до ближайшего целого числа. Процедуру квантования осуществляет устройство с амплитудной характеристикой ступенчатого вида, которое называется квантователем. Амплитудная характеристика квантователя изображена на рис. 3.7.

При реализации квантователя диапазон изменения уровня дискретного сигнала разбивается на уровней (включая нулевой), каждый из которых отличается от соседних на величину , называемую шагом квантования.

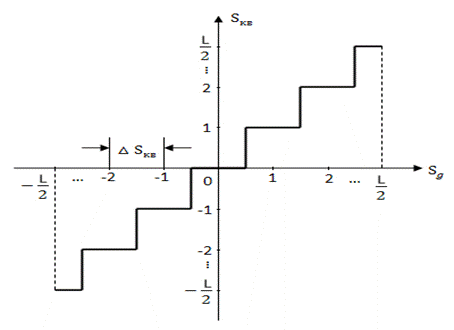
Рис. 3.7

Таким образом, максимальное и минимальное значения квантованного сигнала соответственно равны

, .

В процессе квантования значение в момент времени сравнивается со значением , где . Квантованный сигнал принимает значение

, (3.18)

если

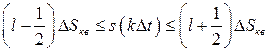. (3.19)

Отметим, что значение запоминается до момента следующего отсчёта дискретного сигнала.

Процедура квантования показана на рис. 3.8.

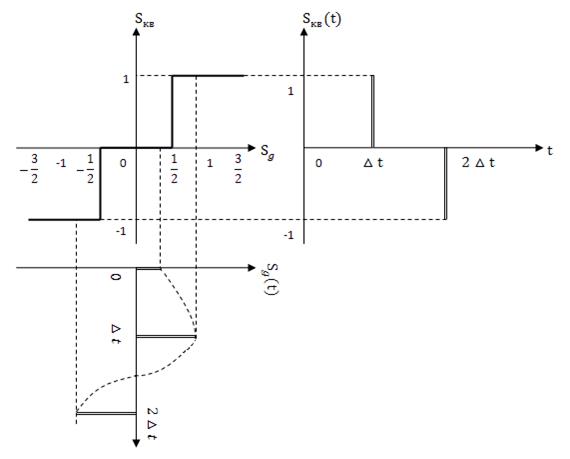
Рис. 3.8

На этом рисунке изображены фрагмент амплитудной характеристики квантователя, дискретный сигнал , временная диаграмма которого повёрнута на для удобства пояснения процедуры квантования, и квантованный сигнал .

Поясним процедуру квантования. Рассмотрим отсчёт . Поскольку значение этого отсчёта находится в интервале , в соответствии с (3.18) значение квантованного сигнала будет равно , т.к. условие (3.19) выполняется при . Значение отсчёта , как это следует из рисунка, находится в пределах , т.е. условие (3.19) выполняется при , поэтому значение квантованного сигнала . И, наконец, значение отсчёта находится в интервале 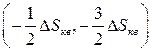, а значение квантованного сигнала .

Ввиду того, что при квантовании осуществляется фактически округление значений , квантованный сигнал будет отличаться от дискретного. При этом искажения, вносимые квантователем

, (3.20)

принципиально неустранимы. Поэтому, при преобразовании непрерывного сигнала в цифровой необходимо оценивать степень искажений, вносимых квантователем.

Искажения, вносимые квантователем, целесообразно оценивать величиной среднеквадратичной ошибки. При исследовании процедур квантования было установлено, что величина среднеквадратичной ошибки

.

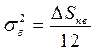Таким образом, ошибка квантования тем меньше, чем меньше шаг квантования .

Физически при преобразовании реальных сигналов проявляется в виде шума. Поэтому искажения получили название шума квантования.

Сигнал на выходе квантователя уже представляет собой цифровой сигнал, однако, представленный в -ичной системе счисления. Напомним, что любое число может быть представлено в системе счисления с основанием следующим образом:

,

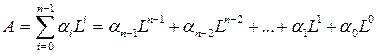где принимает значение из совокупности значений от до ;

– значность числа (количество разрядов, которым представлено число).

Так, например, число в десятичной системе счисления, т.е. при , записывается следующим образом

.

Нетрудно убедится в том, что любое значение на промежутке времени от момента до момента (вспомним замечание о том, что значение запоминается) равно

.

Иными словами, квантованный сигнал представлен одноразрядным числом в -ичной системе счисления. Так как - число уровней квантования, которое выбирается довольно большим, осуществлять передачу и обработку такого сигнала средствами вычислительной техники, которые оперируют в подавляющем большинстве случаев с числами в двоичной системе счисления, неудобно. Поэтому квантованный сигнал, как число, необходимо перевести из - ичной системы в некоторую другую, более удобную с точки зрения дальнейшей передачи и обработки, систему счисления. Эта операция называется кодированием.

Перевод числа из одной системы счисления в другую сопровождается изменением разрядности числа. Соотношение разрядности числа, представленного в системах с основаниями и определяются формулой

.

Поэтому, при переводе числа из системы с основанием в систему с основанием число разрядов будет равно

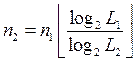, (3.21)

где знак означает округление до ближайшего верхнего целого числа.

Практикой установлено, что для передачи речевого сигнала в цифровой форме необходимо 256 уровней квантования. Эта величина принята в качестве международного стандарта. Значит, при квантовании речевого сигнала значение будет представлено одним разрядом в 256-ричной системе счисления. Для дальнейшей передачи и обработки эти числа обычно переводят в двоичную систему счисления. При этом количество разрядов числа , в соответствии с (3.21), составит

,

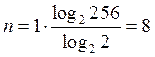а значение каждого разряда может быть или нулем, или единицей.

Таким образом, в результате кодирования квантованный сигнал принимает форму двоичной последовательности, называемой кодовой комбинацией или кодовым словом.

На рис. 3.9 в качестве примера представлен квантованный сигнал при числе уровней квантования и кодовые слова для значений и . Очевидно при в соответствии с (3.21) число разрядов кодового слова составит

.

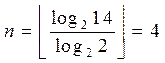Тогда при кодировании значения образуется кодовое слово 1101, а при кодировании кодовое слово 0101.

Отметим, что минимальное значение квантованного сигнала в рассмотренном случае кодируется кодовым словом 0000 .

Если физически разряд кодового слова представлен в виде прямоугольного импульса амплитудой , то двоичный цифровой сигнал будет иметь вид представленный на рис. 3.9, б.

Длительность кодовой комбинации цифрового двоичного сигнала, очевидно должна быть равна т.е. интервалу дискретизации. Отсюда длительность элемента (разряда) кодовой комбинации

.

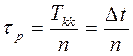Выше было отмечено, что для уменьшения ошибки квантования необходимо уменьшать величину шага квантования . Однако при этом увеличивается число уровней, что в свою очередь приводит к увеличению разрядности кодовой комбинации цифрового сигнала, уменьшению длительности разряда и, следовательно, расширению спектра цифрового сигнала. Это обстоятельство необходимо учитывать при проектировании систем передачи цифровых сигналов по каналам связи.

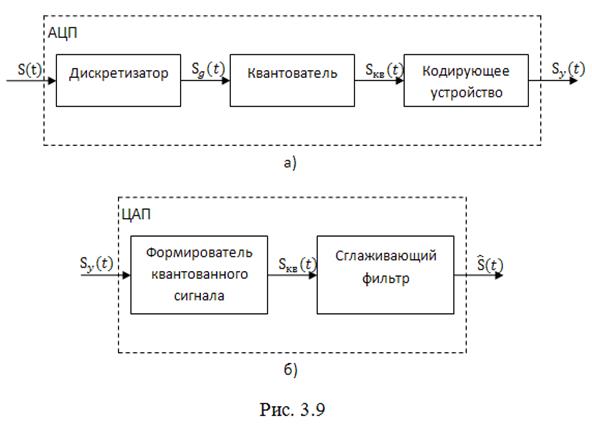
На практике операции дискретизации, квантования и кодирования осуществляются в одном устройстве называемом аналого-цифровым преобразователем (АЦП). Структурная схема АЦП представлена на рис. 3.9, а. На схеме показаны основные элементы АЦП и сигналы на их входах.

Операция обратного преобразования цифрового сигнала в аналоговый выполняется цифро-аналоговым преобразователем (ЦАП), схема которого представлена на рис. 3.9, б, и предусматривает ряд этапов.

В первую очередь цифровой двоичный сигнал подвергается поразрядному взвешенному (с «весом» ) суммированию, в результате чего в моменты времени формируется квантованный сигнал . После этого последовательность значений квантованного сигнала поступает на сглаживающий фильтр с амплитудно-частной характеристикой

в пределах полосы пропускания или . Как известно из предыдущего материала, при поступлении на вход фильтра сигнала в виде короткого импульса амплитудой , сигнал на выходе будет иметь вид

.

Сложение откликов фильтра дает сигнал ŝ(t). Следует подчеркнуть, что восстановленный сигнал ŝ(t) будет отличатся от исходного ввиду наличия ошибки квантования.