4.4.1. Обобщенное представление сигналов с угловой модуляцией

4.4.2. Сигналы с частотной модуляцией

4.4.1. Обобщенное представление сигналов с угловой модуляцией

В предыдущем разделе была рассмотрена процедура модуляции, когда информационным параметром, изменяемым в соответствии с законом управляющего (модулирующего) сигнала являлась амплитуда несущего колебания. Однако помимо амплитуды несущее колебание характеризуется также частотой и начальной фазой

, (4.20)

где – полная фаза несущего колебания, которая определяет текущее значение фазового угла.

Изменение либо , либо в соответствии с управляющим сигналом соответствует угловой модуляции. Таким образом, понятие угловой модуляции включает в себя как частотную (ЧМ), так и фазовую (ФМ) модуляцию.

Рассмотрим обобщенные аналитические соотношения для сигналов с угловой модуляцией. При частотной модуляции в соответствии с управляющим сигналом изменяется мгновенная частота несущего колебания в пределах от нижней до граничных частот

. (4.21)

Наибольшее значение частотного отклонения от называется девиацией частоты

.

Если граничные частоты расположены симметрично относительно , то девиация частоты

. (4.22)

Именно такой случай частотной модуляции будет рассматриваться в дальнейшем.

Закон изменения полной фазы определяется как интеграл от мгновенной частоты. Тогда, с учетом (4.21) и (4.22), можно записать

. (4.23)

Подставляя (4.23) в (4.20), получим обобщенное аналитическое выражение сигнала с частотной модуляцией

. (4.24)

Слагаемое представляет собой составляющую полной фазы, обусловленную наличием частотной модуляции. Нетрудно убедится в том, что полная фаза сигнала с частотной модуляцией изменяется по закону интеграла от .

При фазовой модуляции, в соответствии с модулирующем сигналом , изменяется начальная фаза несущего колебания в пределах от нижнего до верхнего граничных значений фазы

. (4.25)

Наибольшее отклонение фазового сдвига от называется девиацией фазы . Если и расположены симметрично относительно , то . В этом случае полная фаза сигнала с фазовой модуляцией

. (4.26)

Тогда, подставляя (4.26) в (4.20), получим обобщенное аналитическое выражение сигнала с фазовой модуляцией

. (4.27)

Рассмотрим, как изменяется мгновенная частота сигнала при фазовой модуляции. Известно, что мгновенная частота и текущая пол-

ная фаза связаны соотношением

.

Подставляя в это выражение формулу (4.26) и проведя операцию дифференцирования, получим

, (4.28)

где – составляющая частоты, обусловленная наличием фазовой модуляции несущего колебания (4.20).

Таким образом, изменение начальной фазы несущего колебания приводит к изменению мгновенных значений частоты по закону производной от по времени.

Практическая реализация устройств формирования сигналов угловой модуляции может осуществляться одним из двух методов: прямым или косвенным. При прямом методе в соответствии с законом изменения управляющего сигнала изменяются параметры колебательного контура генератора несущего колебания. Выходной сигнал при этом оказывается промодулированным по частоте. Для получения сигнала фазовой модуляции на входе частотного модулятора включается дифференцирующая цепь.

Сигналы фазовой модуляции при прямом методе формируются путём изменения параметров колебательного контура усилителя, подключённого к выходу генератора несущего колебания. Для преобразования сигналов фазовой модуляции в сигнал частотной модуляции управляющее колебание подаётся на вход фазового модулятора через интегрирующую цепь.

Косвенные методы не предполагают непосредственного воздействия управляющего сигнала на параметры колебательного контура. Один из косвенных методов базируется на преобразовании амплитудно-модулированных сигналов в сигналы фазовой модуляции, а те, в свою очередь, - в сигналы частотной модуляции. Более подробно, вопросы формирования сигналов частотной и фазовой модуляции будут рассмотрены ниже.

4.4.2. Сигналы с частотной модуляцией

Анализ характеристик сигналов с угловой модуляцией мы начнём с рассмотрения однотональной частотной модуляции. Управляющий сигнал в этом случае представляет собой колебание единичной амплитуды (к этому виду всегда можно привести )

, (4.29)

а модулируемым параметром несущего колебания является мгновенная частота. Тогда, подставляя (4.29) в (4.24), получим:

.

Выполнив операцию интегрирования, приходим к следующему выражению сигнала однотональной частотной модуляции

. (4.30)

Отношение

называется индексом частотной модуляции и имеет физический смысл части девиации частоты , приходящуюся на единицу частоты модулирующего сигнала. Так например, если девиация частоты несущего колебания МГц составляет , а частота управляющего сигнала кГц, то индекс частотной модуляции составит . В выражении (4.30) начальная фаза не учитывается как не имеющая принципиального значения.

Временная диаграмма сигнала при однотональной ЧМ представлена на рис. 4.7

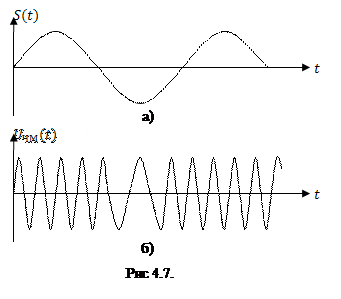
Рассмотрение спектральных характеристик ЧМ-сигнала начнём с частного случая малого индекса частотной модуляции . Воспользовавшись соотношением

,

представим (4.30) в виде

(4.31)

Поскольку , то можно воспользоваться приближёнными представлениями

; при .

Тогда

,

и выражение (4.31) приобретает вид

.

Воспользовавшись известным тригонометрическим соотношением

и полагая и , получим:

(4.32)

или

. (4.33)

Это выражение напоминает выражение (4.6) для однотонального АМ – сигнала. Отличие состоит в том, что, если в однотональном АМ – сигнале начальные фазы боковых составляющих одинаковы, то в однотональном ЧМ сигнале при малых индексах частотной модуляции они отличаются на угол , т.е. находятся в противофазе.

Спектральная диаграмма такого сигнала показана на рис. 4.8

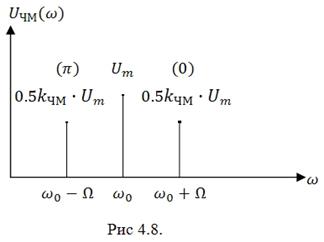В скобках указаны значения начальной фазы боковых составляющих. Очевидно, ширина спектра ЧМ – сигнала при малых индексах частотной модуляции равна

.

Сигналы с частотной модуляцией с малым в практической радиотехнике применяются достаточно редко.

В реальных радиотехнических системах индекс частотной модуляции существенно превышает единицу.

Так например, в современных аналоговых системах мобильной связи, использующих для передачи речевых сообщений сигналы частотной модуляции при верхней частоте речевого сигнала кГц и девиации частоты кГц, индекс , как нетрудно убедиться, достигает значения ~3-4. В системах же радиовещания метрового диапазона индекс частотной модуляции может превышать значения, равного 10. Поэтому рассмотрим спектральные характеристики ЧМ сигналов при произвольных значениях величины .

Возвратимся к выражению (4.32). Известны следующие виды разложения

(4.34)

, (4.35)

где – фунция Бесселя первого рода -го порядка.

Подставляя эти выражения в (4.32), после несложных, но довольно громоздких преобразований с использованием уже неоднократно упомянутых выше соотношений произведений косинусов и синусов, получим

(4.36)

где .

Полученное выражение представляет собой разложение однотонального ЧМ – сигнала на гармонические составляющие, т.е. амплитудный спектр. Первое слагаемое этого выражения является спектральной составляющей колебания несущей частоты с амплитудой . Первая сумма выражения (4.35) характеризует боковые составляющие с амплитудами и частотами , т.е. нижнюю боковую полосу, а вторая сумма – боковые составляющие с амплитудами и частотами , т.е. верхнюю боковую полосу спектра.

Спектральная диаграмма ЧМ – сигнала при произвольном представлена на рис. 4.9.

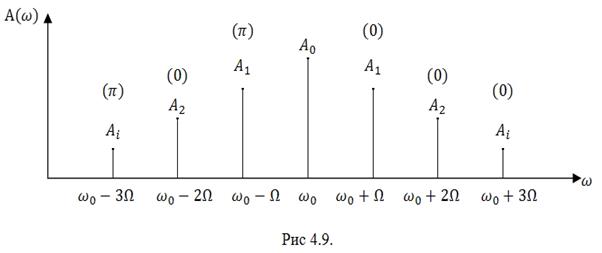
Проанализируем характер амплитудного спектра ЧМ – сигнала. В первую очередь отметим, что спектр является симметричным относительно частоты несущего колебания и теоретически является бесконечным.

Составляющие боковых боковых полос расположены на расстоянии Ω друг от друга, а их амплитуды зависят от индекса частотной модуляции. И наконец, у спектральных составляющих нижней и верхней боковых частот с чётными индексами начальные фазы совпадают, а у спектральных составляющих с нечётными индексами отличаются на угол .

В таблице 4.1 приведены значения функции Бесселя для различных i и . Обратим внимание на составляющую несущего колебания . Амплитуда этой составляющей равна . Из таблицы 4.1 следует, что при амплитуда , т.е. спектральная составляющая несущего колебания в спектре ЧМ – сигнала отсутствует. Но это не означает отсутствия несущего колебания в ЧМ – сигнале (4.30). Просто энергия несущего колебания перераспределяется между составляющими боковых полос.

Таблица 4.1

Как уже подчёркивалось выше спектр ЧМ – сигнала теоретически является бесконечным. На практике же полоса пропускания радиотехнических устройств всегда ограничена. Оценим практическую ширину спектра, при котором воспроизведение ЧМ – сигнала можно считать неискажённым.

Средняя мощность ЧМ – сигнала определяется как сумма средних мощностей спектральных составляющих

.

Проведённые расчёты показали, что около 99% энергии ЧМ – сигнала сосредоточено в частотных составляющих с номерами . А это означает, что частотными составляющими с номерами можно пренебречь. Тогда практическая ширина спектра при однотональной ЧМ с учётом его симметрии относительно

,

а при больших значения

, (4.37)

Т.е. равна удвоенной девиации частоты.

Таким образом, ширина спектра ЧМ – сигнала приблизительно в раз больше ширины спектра АМ – сигнала. Вместе с тем, для передачи информации используется вся энергия сигнала. В этом состоит преимущества сигналов частотной модуляции над сигналами амплитудной модуляции.