Задача 1.
Дана система трёх линейных уравнений. Найти решение её методом Крамера.
2x + 3y + z = 1
- x + 4y + 2z = - 1
x - 2z - 3z = - 3
Решение.
Запишем формулы Крамера: ![]() ;
; ![]() ;
; ![]() .
.
Здесь: D - определитель системы;
D x – определитель, полученный из определителя системы заменой первого столбца на столбец свободных членов;
D y - определитель, полученный из определителя системы заменой второго столбца на столбец свободных членов;
D z – определитель, полученный из определителя системы заменой третьего столбца на столбец свободных членов.
В нашем случае имеем:
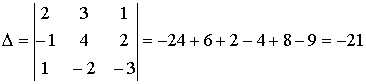 .
.
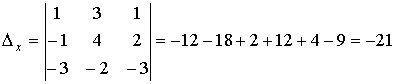 .
.
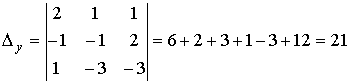 .
.
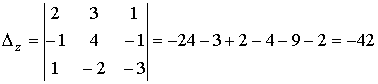 .
.
Теперь найдем значения неизвестных:
![]() ;
; ![]() ;
; ![]() .
.
Для проверки подставим найденные значения неизвестных в исходную систему и убедимся в правильности решения.
Задача 2.
Даны координаты вершины пирамиды ![]() . Сделать
. Сделать
- длину ребра
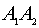 .
. - угол между ребрами
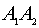 и
и 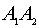
- площадь грани
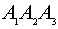
- уравнение прямой
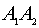
- уравнение плоскости
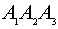
- объем пирамиды
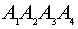
![]() ,
,![]() ,
, ![]() ,
, ![]()
Решение:
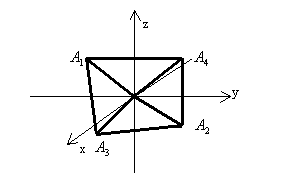
1) Длина ребра ![]() равна расстоянию между точками
равна расстоянию между точками ![]() и
и ![]() или модулю
или модулю
вектора ![]() . Расстояние между точками
. Расстояние между точками ![]() и
и ![]() вычисляется по формуле
вычисляется по формуле ![]()
![]() .
.
Подставляя в эту формулу исходные данные, получим ![]()
2) Угол между ребрами будем искать, используя формулы векторной алгебры:
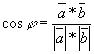
![]()
![]()
![]()
В нашем случае ![]() ,
, ![]() .
.
Чтобы найти координаты вектора, из координат конца вектора следует вычесть координаты начала вектора. Таким образом,
![]()
![]()
![]()
![]()
3) Площадь треугольника ![]() можно найти, используя свойства скалярного произведения: площадь параллелограмма, построенного на векторах
можно найти, используя свойства скалярного произведения: площадь параллелограмма, построенного на векторах ![]() и
и ![]() численно равна модулю их векторного произведения.
численно равна модулю их векторного произведения.
В нашем случае, ![]()
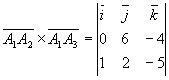 =
=![]() =
=
=![]()
Имеем, ![]()
Итак, площадь грани ![]()
4) Уравнение прямой ![]() найдем как канонические уравнения прямой в пространстве:
найдем как канонические уравнения прямой в пространстве:
![]() ,
,
где ![]() - координаты направляющего вектора прямой, а
- координаты направляющего вектора прямой, а ![]() - координаты точки прямой. В нашем случае
- координаты точки прямой. В нашем случае ![]() , а в качестве точки
, а в качестве точки ![]()
![]() .
.
Итак, уравнение прямой ![]() имеет вид:
имеет вид:
![]() .
.
В общем виде:
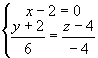 или
или ![]()
5) Уравнение плоскости ![]() будем искать как уравнение плоскости, проходящей через три данные точки
будем искать как уравнение плоскости, проходящей через три данные точки ![]() ,
,![]() и
и ![]() :
:
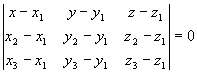 ,
,
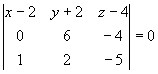 ,
,
![]() .
.
Упрощая, получим: ![]() .
.
6) Объем пирамиды ![]() найдем, используя свойство смешанного произведения трех векторов – модуль смешанного произведения численно равен объему параллелепипеда, построенного на этих векторах. Соответственно
найдем, используя свойство смешанного произведения трех векторов – модуль смешанного произведения численно равен объему параллелепипеда, построенного на этих векторах. Соответственно
![]() .
.
Найдем смешанное произведение векторов ![]() ,
,![]() и
и![]() :
:
![]()
![]()
Ответы:
- длина ребра
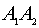 равна
равна 
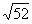 (ед.)
(ед.)
- угол между ребрами
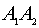 и
и 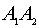 равен
равен 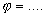
- площадь грани
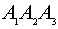 равна 11.58 (кв. ед.)
равна 11.58 (кв. ед.) - уравнение прямой
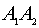 (в каноническом виде ):
(в каноническом виде ):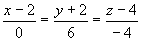
- уравнение плоскости
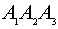 (в общем виде):
(в общем виде): 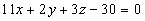
- объем пирамиды
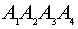 равен 11 (куб. ед.).
равен 11 (куб. ед.).

