Как было установлено выше, между сигналом и его спектром существует однозначная связь, определяемая прямым преобразованием Фурье. Поскольку в процессе передачи сигнала он подвергается различным преобразованиям, очень важно установить как при этом изменяется спектр сигнала. Это имеет большое значение с точки зрения выбора оптимальных методов передачи, приема, требований к параметрам канала связи.

Рассмотрим основные теоремы о спектрах, имеющих практическое применение в электросвязи. Учитывая связь между преобразованием Фурье и Лапласа и имея в виду доказательства основных теорем, остановимся только на физической интерпретации основных теорем спектрального анализа.

Спектр суммы сигналов (теорема линейности) равен сумме спектров этих сигналов. Это свойство является следствием линейности преобразования Фурье. В более общем виде оно может быть записано следующим образом: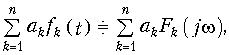

где a_k — коэффициенты разложения; 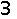— знак соответствия между сигналом и его спектром, определяемого парой преобразований Фурье.

Сдвиг сигнала во времени f(t—t₀) соответствует умножению его спектра на :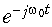

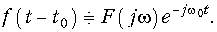
Из (9.28) следует важный вывод о том, что при сдвиге сигнала во времени его амплитудный спектр не изменяется, а фазовый изменяется пропорционально wt₀. Эта теорема имеет большое значение, так как в процессе обработки сигналов часто возникает необходимость осуществлять задержку сигнала.

Изменение масштаба независимого переменного (сжатие сигнала) описывается выражением

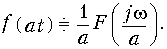
Из (9.29) следует, что сжатие сигнала во времени (а > 1) приводит к расширению спектра сигнала и напротив — растяжение сигнала (а < 1) — к сужению спектра.

Перемножение двух сигналов (теорема свертки). Спектр произведения двух функций f₁(t) и f₂(t) соответствует свертке их спектров F₁(jw) и F₂(jw):

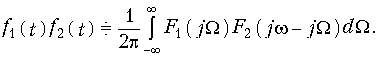
Важное значение имеет обратная теорема о произведении спектров сигналов:

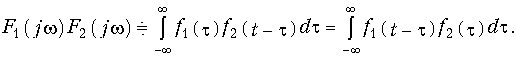
Свертка функций широко использовалась ранее во временных методах анализа электрических цепей.

Дифференцирование и интегрирование сигнала. При дифференцировании сигнала его спектр умножается на оператор jw:

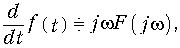
а при интегрировании делится на jw:

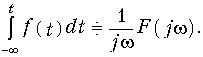
Доказательство (9.32)—(9.33) следует непосредственно из прямого и обратного преобразований Фурье. Следует подчеркнуть, что (9.33) справедливо для сигналов, удовлетворяющих условию F(0) = 0.

Смещение спектра сигнала на частоту 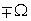соответствует умножению сигнала на оператор :

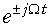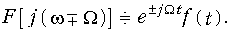
Теорема смещения (9.34) позволяет определить спектр модулированного сигнала и имеет большое значение в теории электрической связи.