3.1. Дрейфовый ток
Когда отсутствует внешнее поле, электроны и дырки находятся в хаотическом движении. При наличии электрического поля на хаотическое движение накладывается компонента направленного движения, т. е. дырки направленно движутся вдоль электрического поля, электроны против, создавая ток одного направления (рисунок 3.1).
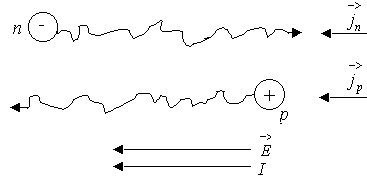
Рисунок 3.1 – Схема движения электронов и дырок под действием внешнего поля.
Ток обусловленный внешним полем напряженностью 
называют дрейфовым. Электронная 
и дырочная 
составляющие плотности дрейфового тока равны следующим выражениям:
,
где 
– заряд электрона, 
и 
– концентрация дырок и электронов:
,
т. е. это выражение закона Ома в дифференциальной форме, где 
и 
подвижности электронов и дырок, т. е. скорости электронов 
и дырок 
, возникающие при напряженности поля 
равном единице:
;
.
Например, при 
К
,
в 
,
в 
3.2. Диффузионный ток
Электрический ток, обусловленный градиентом концентрации носителей называют диффузионным током.
В одномерном случае плотность диффузионного тока электронов и дырок равна следующим выражениям:
где 
и 
– градиент концентрации электронов и дырок, 
и 
– коэффициенты диффузии электронов и дырок, численно равные количеству электронов (или дырок), проходящему через единицу площади в единицу времени при градиенте концентрации носителей равном единице.
Движение носителей заряда происходит в сторону убывания их концентрации (знак минус у дырочной составляющей). Электронная составляющая тока имеет знак (+), т. к. за направление тока принято направление положительного заряда. В общем случае в полупроводниках может быть и электрическое поле и градиент концентрации носителей. Полная плотность тока пи этом равна:
- электронная составляющая тока;
- дырочная составляющая.