К основным видам аналоговой модуляции относятся амплитудная модуляция (AM), фазовая модуляция (ФМ) и частотная модуляция (ЧМ). Разновидностями AM являются балансная (БМ) и однополосная (ОМ) модуляции.

Непосредственная передача. Наиболее простым сигналом для передачи непрерывного сообщения u(t) является сигнал, пропорциональный u(t):

s(t)=Au(t), (3.3)

где А — некоторая постоянная. Такой сигнал соответствует форме (3.1), если в ней положить f(t)=A и М [u(t)]=u(t). Примером такой непосредственной передачи сообщений является обычная телефонная связь по проводам.

Амплитудная модуляция. Для этого вида модуляции: f(t)=,

где т — коэффициент модуляции.

Модулированный сигнал запишется

(3.4)

Это выражение даёт представление реального AM сигнала

Спектр сигнала в общем случае определяется как преобразование Фурье от s(t):

Учитывая, что и

получим

(3.5)

где — спектр передаваемого сообщения. Отсюда видно, что при AM происходит перенос спектра сообщения на частоту (рис. 3.16). Ширина спектра сигнала F при AM в два раза шире спектра сообщения Fm:

При модуляции одним тоном, когда

u(t)=,

(3.6)

Из этого выражения следует, что амплитуда модулированного сигнала изменяется от до , а мощность сигнала соответственно от до

Где мощность несущего колебания. Средняя мощность AM сигнала равна:

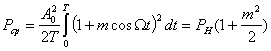
При m=l и Pcp=1,5PH; отношение средней мощности к максимальной равно 0,375. "Эти соотношения указывают на существенный недостаток амплитудной модуляции — плохое использование мощности передатчика.

Балансная модуляция (БМ). Кроме обычной AM применяется передача AM без несущей — балансная модуляция. Для этого вида модуляции:

f(t)=, (3.7)

тогда

(3.8)

Спектр сигнала при БМ

(3.9)

Здесь имеются только две боковые полосы — несущая отсутствует.

При однополосной модуляции (ОМ) передается только одна боковая полоса. Для этого вида модуляции при передаче верхней боковой полосы:

f(t)=, (3.10)

(3.11)

Спектр сигнала ОМ

(3.12)

Действительно, если разложить функции u(t) и (t) в ряд Фурье:

и учесть, что cosx; и sinx являются парой преобразования Гильберта, по получим

Такое представление является аналитическим для всех >0. Замена модуляционной функции [u(t)] на сопряженную ей *[u(t)]=u(t)-i(t) дает форму сигнала s(t), соответствующую нижней боковой полосе.

Системы БМ и ОМ позволяют сократить бесполезный расход энергии на составляющую несущей частоты, а при ОМ дополнительно вдвое сократить ширину спектра передаваемого сигнала. Однако реализация указанных преимуществ требует более сложной аппаратуры.

Угловая модуляция. В случае угловой модуляции (ЧМ и ФМ) модуляционная функция имеет вид

(3.13)

При синусоидальной несущей f(t)=модулированный сигнал будет иметь следующее выражение:

(3.1 4)

Реальный сигнал

(3.15)

Это обычное представление сигнала с угловой модуляцией. Согласно (3.15) полная фаза высокочастотного колебания равна:

(3.16)

а мгновенная частота колебания изменяется по закону производной от , т. е.

(3.17)

Наоборот, при изменении частоты по закону ω(t) (3.17) фаза колебания ψ(t) будет изменяться по закону интеграла от ω(t):

(3.18)

В случае фазовой модуляции . Тогда на основании (3.15) и (3.16) имеем:

(З.19) (3.20)

При частотной модуляции по закону передаваемого сообщения изменяется частота несущего колебания

(3.21)

где— амплитуда частотного отклонения (девиация частоты). Полная фаза колебания при этом будет равна:

(3.22)

Тогда выражение ЧМ сигнала запишется в виде

(3.23)

При модуляции одним тоном, когда и (t)=cosΩt, выражения сигнала при ФМ и ЧМ по форме имеют одинаковый вид:

(3.24)

где т — индекс модуляции: при ФМ при ЧМ

Для определения спектра сигнала заменим в (3.24) косинус суммы двух углов по известным формулам из тригонометрии

(3.25)

Здесь для упрощения записи мы положим =0. Из теории бесселевых функций известны следующие соотношения:

(3.26)

(3.27)

где — бесселева функция первого рода k-гo порядка от аргумента т. После подстановки (3.26) и (3.27) в (3.25) получаем

(3.28)

Таким образом, оказывается, что даже при синусоидальных ЧМ и ФМ получается теоретически безграничный спектр. Он состоит из несущей ω0 и двух боковых полос . Амплитуда несущей А010(т) при ЧМ и ФМ. в отличие от AM, зависит от модулирующего колебания. При некоторых значениях т она может быть вообще равна нулю (т =2,3; 5,4). Амплитуда боковых частот равна . Однако практически ширина спектра ЧМ и ФМ сигналов ограничена.

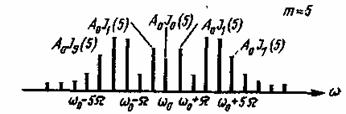
Рис. 3.2. Спектр сигнала с угловой модуляцией

На рис. 3.2 приведен спектр сигнала с угловой модуляцией одним тоном при m=5. Как видим, амплитуды боковых частот быстро убывают с увеличением номера гармоники k. При k>m составляющие спектра малы и ими можно пренебречь. Практически ширина спектра сигнала при угловой модуляции равна F=2(m+l)Fm, где Fт= частота модулирующего колебания.

Различие между ЧМ и ФМ проявляется только при изменении частоты модуляции Ω. При ЧМ т=, поэтому при m>>1 полоса практически не зависит от Fm. При ФМ b

при m>>1 ширина спектра будет равна F=2ΔφfmFm т. е. она зависит от модулирующей частоты Fm. В этом и состоит различие в спектрах ЧМ и ФМ.

В случае малого индекса модуляции спектр ЧМ и ФМ сигналов, так же как и в случае AM, имеет только три составляющие:

(3.29)

Это непосредственно следует из (3.28), если учесть, что при m<<l sin (msinΩt)msinΩt, а cos (msinΩt)1.

Сравнение (3.6) и (3.29) показывает, что различие спектров сигналов при AM и угловой модуляции заключается только в сдвиге фазы колебания нижней боковой частоты на 180° относительно его положения при AM. Это различие существенно и иллюстрируется векторными диаграммами, изображенными на рис. 3.3.

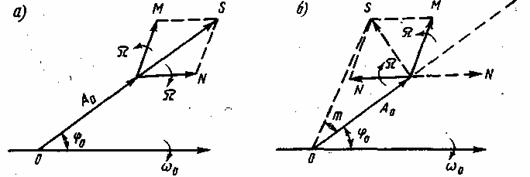
Рис. 3.3. Векторные диаграммы: AM сигнала (а), ЧМ сигнала (ш<1) (б)

Однополосная угловая модуляция. Если функция — аналитическая:

то сигнал

(3.30)

также является аналитической функцией при . Он не содержит отрицательных частот, хотя и имеет бесконечный спектр в области положительных частот:

(3.31)

Выражение (3.30) определяет новый модулированный сигнал. Этот сигнал представляет собой вариант сигнала однополосной угловой модуляции. Для доказательства этого рассмотрим случай частотной модуляции одним тоном u(t)=sinΩt. Для этого случая функция φ(t) и ее преобразование Гильберта принимают вид:

Где индекс модуляции. Модулирующая функция при этом преобразуется к виду

, а модулированный сигнал

Отсюда видно, что спектр модулированного сигнала состоит из одной боковой полосы частот. Сигнал однополосной ЧМ можно получить из обычного ФМ сигнала путем преобразования Гильберта (например, посредством фазового сдвига на ) и модуляции амплитуды по экспоненциальному закону. Тогда ограничение такого сигнала в приемнике восстановит нижнюю боковую полосу частот и позволит применить для детектирования обычный дискриминатор.