4.4.1. Когерентное обнаружение сигналов PSK
4.4.2. Цифровой согласованный фильтр
4.4.1. Когерентное обнаружение сигналов PSK
На рис. 4.7 показан детектор, который может использоваться для когерентного обнаружения любого цифрового сигнала. Подобный корреляционный детектор часто называется детектором, работающим по критерию максимального правдоподобия (maximum likelihood detector). Рассмотрим следующую бинарную модуляцию PSK (BPSK). Пусть
![]() (4.21,а)
(4.21,а)
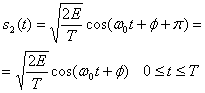 (4.21,б)
(4.21,б)
n(t) — случайный белый гауссов процесс с нулевым средним.
Здесь фазовый член φ — произвольная константа, которую мы для удобства положим равной нулю. Параметр Е — это энергия сигнала, приходящаяся на символ, а Т — длительность символа. Для данного антиподного случая требуется единственная базисная функция. Используя формулы (3.10) и (3.11) и предполагая пространство ортонормированным (т.е. Kj= 1), базисную функцию ![]() можно выразить следующим образом.
можно выразить следующим образом.
![]() (4.22)
(4.22)
Следовательно, переданный сигнал si(t) можно выразить через функцию ![]() и коэффициенты
и коэффициенты ![]() .
.
![]() (4.23,а)
(4.23,а)
![]() (4.23,б)
(4.23,б)
![]() (4.23,в)
(4.23,в)
Предположим, что был передан сигнал s1(t). Тогда математические ожидания на выходах интеграторов произведений, изображенных на рис. 4.7, б, при опорном сигнале ![]() имеют следующий вид.
имеют следующий вид.
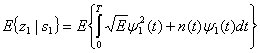 (4.24,а)
(4.24,а)
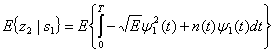 (4.24,б)
(4.24,б)
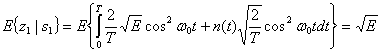 (4.25,а)
(4.25,а)
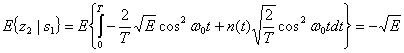 (4.25,б)
(4.25,б)
Здесь ![]() обозначает среднее по ансамблю, так называемое математическое ожидание (expected value). В уравнении (4.25) E{n(t)} = 0. На этапе принятия решения, путем определения местоположения переданного сигнала в сигнальном пространстве, необходимо определить значение данного сигнала. В приведенном примере, где в качестве базисной функции была взята
обозначает среднее по ансамблю, так называемое математическое ожидание (expected value). В уравнении (4.25) E{n(t)} = 0. На этапе принятия решения, путем определения местоположения переданного сигнала в сигнальном пространстве, необходимо определить значение данного сигнала. В приведенном примере, где в качестве базисной функции была взята ![]() , значения
, значения ![]() равны
равны ![]() .Сигналы-прототипы
.Сигналы-прототипы ![]() аналогичны опорным сигналам
аналогичны опорным сигналам ![]() , с точностью до нормирующего множителя. На этапе принятия решения выбирается сигнал с большим значением zi(T). Следовательно, в приведенном выше примере принятый сигнал определен как s1(t). Вероятность ошибки при подобном когерентном обнаружении сигналов BPSK рассмотрена в разделе 4.7.1.
, с точностью до нормирующего множителя. На этапе принятия решения выбирается сигнал с большим значением zi(T). Следовательно, в приведенном выше примере принятый сигнал определен как s1(t). Вероятность ошибки при подобном когерентном обнаружении сигналов BPSK рассмотрена в разделе 4.7.1.
4.4.2. Цифровой согласованный фильтр
В разделе 3.2.2 рассматривалась основная особенность согласованного фильтра — то, что его импульсная характеристика представляет собой запаздывающую версию зеркального отображения (поворота относительно оси t = 0) входного сигнала. Таким образом, если сигнал равен s(t), его зеркальное отображение имеет вид s(-t), а зеркальное отображение, запаздывающее на Т секунд, имеет вид s(T-t). Следовательно, импульсная характеристика h(t), соответствующая сигналу s(t), будет равна следующему.
![]() (4.26)
(4.26)
На рис. 4.7 и 4.8 представлена основная функция коррелятора — интегрирование произведения принятого зашумленного сигнала с каждым опорным сигналом и определение наилучшего соответствия. Схемы, показанные на этих рисунках, подразумевают использование аналоговой аппаратуры (умножителей и интеграторов) и непрерывных сигналов. На них не отражена возможность реализации коррелятора или согласованного фильтра (matched filter — MF) с использованием цифровых технологий и дискретных сигналов. Пример подобной реализации приведен на рис. 4.10, где показан согласованный фильтр, использующий цифровую аппаратуру. Входной сигнал r(t) состоит из сигнала-прототипа s,(t) и шума n(i); ширина полосы сигнала W= 1/2T, где Т — длительность передачи символа. Таким образом, минимальная частота дискретизации по Найквисту равна fs = 2W= 1/T, а время взятия выборки (Ts) должно быть не больше времени передачи символа. Другими словами, на символ должно приходиться не менее одной выборки. В реальных системах подобная дискретизация производится с частотой, в 4 или более раз превышающей минимальную частоту Найквиста. Платой за это является не увеличение полосы передачи, а увеличение быстродействия процессора. В моменты t = kTs выборки (как показано на рис. 4.10, а) сдвигаются в регистре, так что более ранние из них располагаются правее. При дискретизации (взятии выборки) полученного сигнала непрерывное время t заменяется дискретным kTs или просто k, что дает право использовать дискретную запись.
![]()
Здесь индекс i определяет символ из М-арного набора (в нашем случае — двоичного), a k — дискретное время. На рис. 4.10 согласованный фильтр аппроксимируется регистром сдвига с весовыми коэффициентами с/(п), где п=0,...,N-1 — временной индекс весовых коэффициентов и разрядов регистра. В приведенном примере число разрядов регистра и количество выборок на символ равны 4. Итак, суммирование, показанное на рисунке, происходит в моменты времени от n = 0 до n = 3. Из расположения сумматора на схеме понятно что решение относительно значения принятого сигнала принимается после заполнения регистра 4 выборками. Отметим, что для простоты в примере на рис. 4.10, б выборки si(k) могут принимать только три значения (0, ±1). В реальных системах каждая выборка (и весовой коэффициент) — это 6-10 бит. Множеству весовых коэффициентов фильтра {ci(n)} соответствует импульсная характеристика фильтра; согласование весовых коэффициентов с выборками сигнала производится согласно дискретному варианту уравнения (4.26).
![]() (4.27)
(4.27)
Использование дискретной формы интеграла свертки из уравнения (А.44,6) позволяет записать выражение с выхода коррелятора в момент времени, соответствующий k-й. выборке.
![]() (4.28)
(4.28)
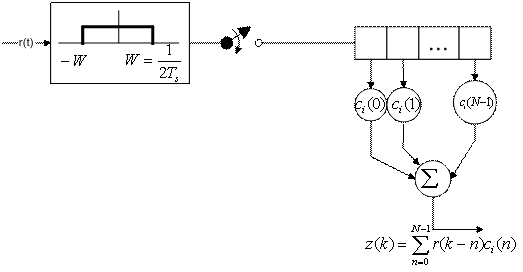
а)
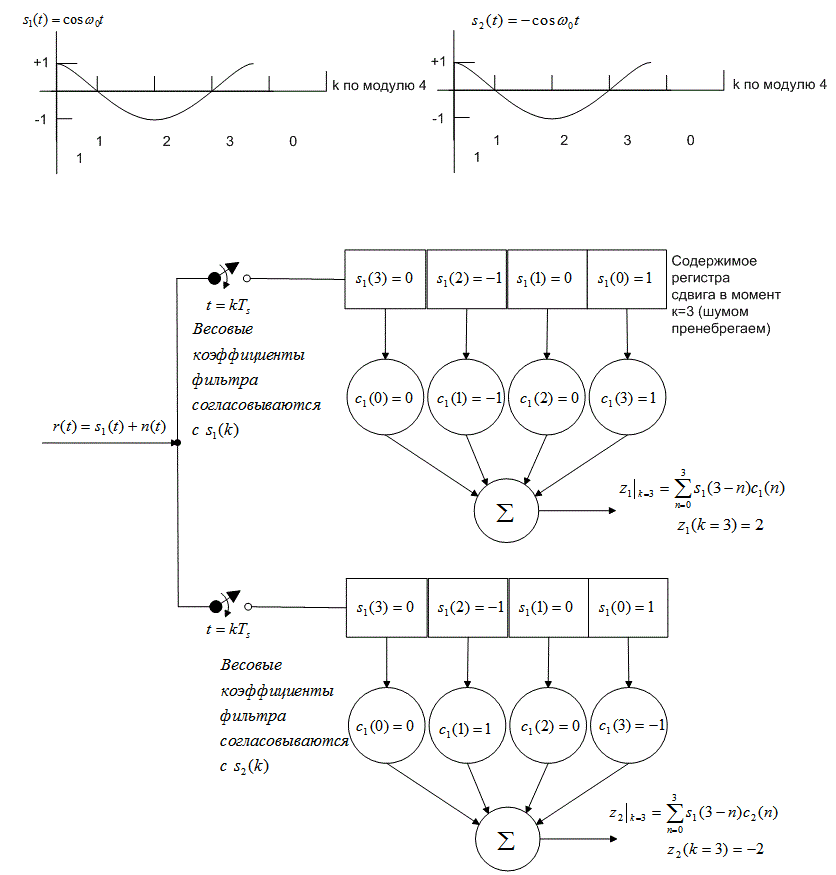 б)
б)
Рис. 4.10. Цифровой согласованный фильтр: а) дискретный согласованный фильтр; б) пример обнаружения с использованием дискретного согласованного фильтра (шумом пренебрегаем)
Здесь х по модулю у — это остаток деления х на у, индекс k — время принятия выборок и выхода фильтра, an — фиктивная переменная времени. В формуле (4.28) выражение r(k-n) содержит п, которое можно рассматривать как "возраст" выборки (как давно она находится в фильтре). В выражении сi(п) л удобно рассматривать как адрес весового коэффициента. Предполагается, что система синхронизирована и упорядочение символов во времени известно. Также предполагается, что шум имеет нулевое среднее, так что математическое ожидание принятой выборки равно следующему.
![]()
Следовательно, при передаче si(t) математическое ожидание выхода согласованного фильтра равно следующему.
![]() (4.29)
(4.29)
На рис. 4.10, б, где сигналы-прототипы изображены как функции времени, видим, что крайняя слева выборка (амплитуда, равная +1) графика s1(t) представляет выборку в момент времени k = 0. Предполагая, что передан был сигнал s1(t) и для упрощения записи мы пренебрегли шумом, можем записать принятую выборку r(k) как s1(k). Выборки заполняют разряды согласованного фильтра, и в конце каждого периода передачи символа в крайнем правом разряде каждого регистра расположена выборка k=0. Отметим, что в формулах (4.28) и (4.29) временные индексы п эталонных весовых коэффициентов расположены в порядке, обратном к временному индексу k - п выборок, что является ключевой особенностью интеграла свертки. То, что наиболее ранняя выборка теперь соответствует крайнему справа весовому коэффициенту, обеспечивает значащую корреляцию. Даже если действия согласованного фильтра мы математически опишем как свертку сигнала с импульсной характеристикой фильтра, конечный результат будет корреляцией сигнала с копией самого себя. По этой причине коррелятор можно реализовать как согласованный фильтр.
На рис. 4.10, б обнаружение, происходящее после выхода сигнала с согласованного фильтра, осуществляется обычным образом. Для принятия двоичного решения выходы z/(£) изучаются при каждом значении k=N-l, соответствующем концу символа. При условии передачи st(t) и пренебрежении шумом, уравнения (4.27)-(4.29) можно объединить и записать выходы коррелятора в моменты времени k =
= N -1=3.
![]() (4.30,а)
(4.30,а)
![]() (4.30,б)
(4.30,б)
Поскольку z1 (k = 3) больше z2(k = 3), детектор принимает решение, что передан был символ s1(t).
Может возникнуть вопрос: чем согласованный фильтр на рис. 4.10, б отличается от коррелятора на рис. 4.8. В случае согласованного фильтра в ответ на каждую новую выборку на входе появляется новое значение на выходе; следовательно, выход представляет собой временной ряд, такой как на рис. 3.7, б (последовательность возрастающих положительных и отрицательных корреляций с входной синусоидой). Подобную последовательность на выходе согласованного фильтра можно получить при использовании нескольких корреляторов, работающих на разных начальных точках входящего временного ряда. Отметим, что за время передачи символа на выходе коррелятора получаем максимальное значение сигнала в момент времени Т (см. рис. 3.7, б). Если синхронизировать согласованный фильтр и коррелятор, их выходы в конце периода передачи символа будут идентичными. Важным отличием между согласованным фильтром и коррелятором является то, что поскольку на выходе коррелятора получаем одно значение на символ, он должен использовать дополнительную информацию, например, относительно моментов начала и завершения интегрирования произведения. При наличии ошибок синхронизации дискретный сигнал, подаваемый с коррелятора на детектор, может быть сильно искажен. С другой стороны, поскольку на выходе согласованного фильтра получаем временной ряд выходных значений (отражающих смещенные во времени входящие выборки, умноженные на фиксированные весовые коэффициенты), использование дополнительной схемы позволяет определить моменты, наиболее подходящие для дискретизации выхода согласованного фильтра.
Пример 4.1. Цифровой согласованный фильтр
Рассмотрим набор сигналов
![]()
где k =0,1,2,3.
Опишите, как цифровой согласованный фильтр (рис. 4.10) может использоваться для обнаружения принятого сигнала, скажем s1(t), при отсутствии шума.
Решение
Вначале сигнал s1(i) преобразуется в набор выборок ![]() . Приемник цифрового согласованного фильтра, как показано на рис. 4.10, б, представляет собой две ветви. Верхняя ветвь состоит из регистра сдвига и коэффициентов, согласовывающихся с точками дискретизации
. Приемник цифрового согласованного фильтра, как показано на рис. 4.10, б, представляет собой две ветви. Верхняя ветвь состоит из регистра сдвига и коэффициентов, согласовывающихся с точками дискретизации ![]() . Подобным образом нижняя ветвь состоит из регистра сдвига и коэффициентов, согласовывающихся с точками дискретизации
. Подобным образом нижняя ветвь состоит из регистра сдвига и коэффициентов, согласовывающихся с точками дискретизации ![]() . В четырех равномерно расположенных точках выборки (k = 0, 1,2, 3) сигналы
. В четырех равномерно расположенных точках выборки (k = 0, 1,2, 3) сигналы ![]() имеют следующие значения.
имеют следующие значения.
![]()
Коэффициенты сi(n) представляют запаздывающий зеркальный поворот сигнала, с которым согласовывается фильтр. Следовательно, ![]() так что можно записать
так что можно записать ![]() .
.
Рассмотрим верхнюю ветвь рис. 4.10, б. В момент времени k = 0 первая выборка s1(k = 0) =0 поступает в крайний левый разряд каждого регистра. В следующий дискретный момент времени k=1 вторая выборка s1(k= l)=A/4 поступает в крайний левый разряд каждого регистра; в то же время первая выборка сдвигается в ближайший справа разряд каждого регистра и т.д. В момент k =3 в крайний левый разряд поступает выборка s1(k = 3) = ЗА/4; к. этому моменту первая выборка сдвинута к крайнему правому разряду. Четыре выборки сигнала теперь расположены в регистрах в зеркальном порядке по отношению к времени их создания. Таким образом, при данном расположении поступающих выборок сигнала и опорных коэффициентов выход сумматора естественным образом описывается операцией свертки и максимизирует корреляцию в соответствующей ветви.
4.4.3. Когерентное обнаружение сигналов MPSK
На рис. 4.11 показан вид сигнального пространства для набора сигналов в модуляции MPSK (multiple phase-shift keying — многофазная манипуляция); на рисунке представлена четырехуровневая (М = 4) фазовая манипуляция, или двукратная фазовая манипуляция (quadriphase shift keying — QPSK). Двоичные цифры в передатчике группируются по две, и в каждом интервале передачи символов две последовательные цифры определяют, какой из четырех возможных сигналов произведет модулятор. Для типичных когерентных М-уровневых систем PSK (MPSK) сигнал si(t) можно выразить следующим образом.
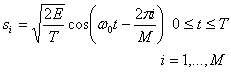 (4.31)
(4.31)
Здесь Е — энергия, полученная сигналом за время передачи символа Т, а ω0 — несущая частота. Предполагая пространство ортонормированным и используя формулы (3.10) и (3.11), можно выбрать следующие удобные оси.
![]() (4.32,а)
(4.32,а)
и
![]() (4.32,б)
(4.32,б)
Здесь, как и в разделе 4.4.1, амплитуда ![]() нормирует ожидаемый выход детектора.
нормирует ожидаемый выход детектора.
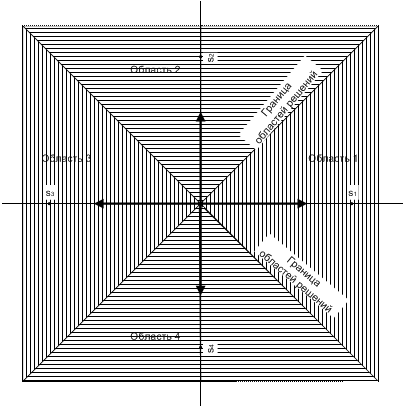
Рис. 4.11. Сигнальное пространство и области решений для системы QPSK
Запишем сигнал si(t) через выбранные ортонормированные координаты.
![]() (4.33,а)
(4.33,а)
![]() (4.33,б)
(4.33,б)
Отметим, что формула (4.33) выражает набор М многофазных сигналов (в общем случае не ортогональный) всего через два ортогональных несущих компонента. Случай М = 4 (QPSK) является уникальным среди множества сигналов MPSK в том смысле, что сигналы QPSK представляются комбинацией антиподных и ортогональных членов. Границы областей решений разбивают сигнальное пространство на M=4 области; процедура разбития подобна описанной в разделе 4.3.1 и изображенной на рис. 4.6 для М = 2. Правило принятия решения для детектора (рис. 4.11) звучит следующим образом: если вектор принятого сигнала попадает в область 1 — отнести его к s1(t); если вектор принятого сигнала попадает в область 2 — выбрать сигнал s2(t) и т.д. Другими словами, правило принятия решения заключается в выборе i-го сигнала, если zi(T) является наибольшим из выходов корреляторов (см. рис. 4.7).
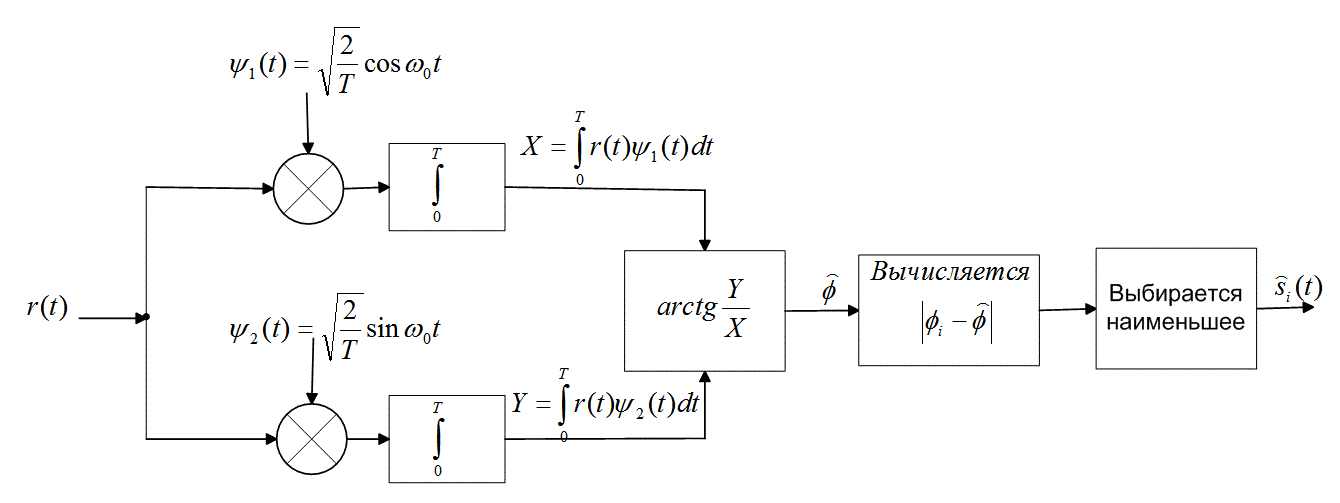
Рис. 4.12. Демодулятор сигналов MPSK
Структура коррелятора, изображенного на рис. 4.7, а, подразумевает использование для демодуляции сигналов MPSK M корреляторов произведений. Также предполагается, что для каждой из M ветвей был соответствующим образом выбран опорный сигнал (т.е. сигнал, имеющий требуемый сдвиг фаз). Стоит отметить, что на практике реализация демодулятора MPSK, согласно схеме на рис. 4.7, б, требует всего N=2 интеграторов произведений, вне зависимости от размера множества сигналов М. Такая экономия позволительна вследствие того, что, как показано в разделе 3.1.3, любой произвольный интегрируемый набор сигналов можно выразить в виде линейной комбинации ортогональных сигналов. Пример подобного демодулятора приведен на рис. 4.12. Объединив формулы (4.32) и (4.33), можно записать принятый сигнал r(t) следующим образом.
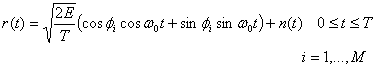 (4.34)
(4.34)
Здесь ![]() , a n(t) — гауссов процесс шума с нулевым средним. Отметим, что на рис. 4.12 изображены только два опорных сигнала (или две базисные функции) —
, a n(t) — гауссов процесс шума с нулевым средним. Отметим, что на рис. 4.12 изображены только два опорных сигнала (или две базисные функции) —
![]() для верхнего коррелятора и
для верхнего коррелятора и ![]() для нижнего. Верхний коррелятор вычисляет функцию
для нижнего. Верхний коррелятор вычисляет функцию
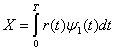 (4.35)
(4.35)
а нижний — функцию
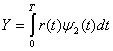 (4.36)
(4.36)
На рис. 4.13 показано, что определение фазы принятого сигнала ![]() производится путем вычисления арктангенса Y/X, где X — синфазный, Y — квадратурный компонент принятого сигнала, а
производится путем вычисления арктангенса Y/X, где X — синфазный, Y — квадратурный компонент принятого сигнала, а ![]() — зашумленная оценка переданной фазы
— зашумленная оценка переданной фазы ![]() . Другими словами, с верхнего коррелятора (рис. 4.12) поступает на выход X, значение синфазной проекции вектора r, а с нижнего — Y, значение квадратурной проекции вектора r, где r — векторное представление r(t). Сигналы X и Y с корреляторов поступают в блок "arctg (Y/X)". Полученное значение фазы
. Другими словами, с верхнего коррелятора (рис. 4.12) поступает на выход X, значение синфазной проекции вектора r, а с нижнего — Y, значение квадратурной проекции вектора r, где r — векторное представление r(t). Сигналы X и Y с корреляторов поступают в блок "arctg (Y/X)". Полученное значение фазы ![]() сравнивается с каждой фазой-прототипом
сравнивается с каждой фазой-прототипом ![]() . Далее демодулятор выбирает фазу
. Далее демодулятор выбирает фазу ![]() ближайшую к
ближайшую к ![]() . Другими словами, демодулятор вычисляет |
. Другими словами, демодулятор вычисляет |![]() -
- ![]() | для каждого прототипа
| для каждого прототипа ![]() и выбирает
и выбирает ![]() , дающую наименьший выход.
, дающую наименьший выход.
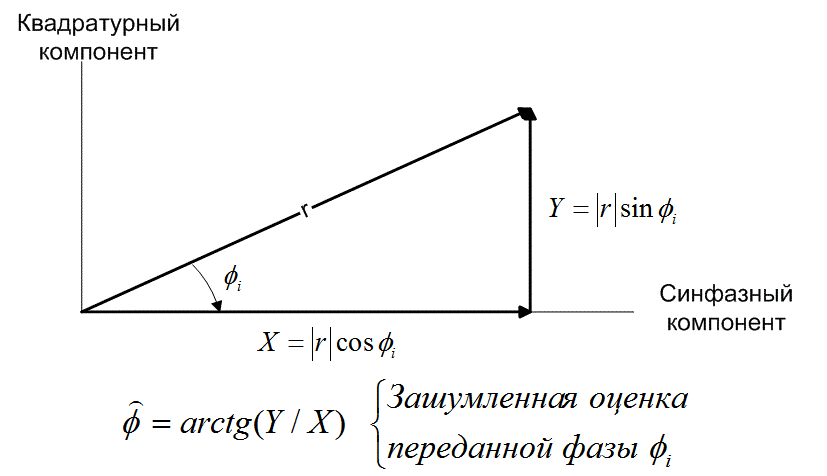
Рис. 4.13. Синфазный и квадратурный компоненты вектора принятого сигнала r
4.4.4. Когерентное обнаружение сигналов FSK
При использовании схемы FSK информация модулируется частотой несущей. Типичный вид набора сигналов FSK выражается формулой (4.8)
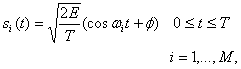
где Е — энергия, переданная сигналу ![]() в течение времени передачи символа Т; кроме того,
в течение времени передачи символа Т; кроме того, ![]() обычно выбирается кратным
обычно выбирается кратным ![]() . Фазовый член φ — это произвольная константа, которую можно положить равной нулю. Предполагая, что базисные функции
. Фазовый член φ — это произвольная константа, которую можно положить равной нулю. Предполагая, что базисные функции ![]() формируют ортонормированное множество, можно получить более удобное выражение для
формируют ортонормированное множество, можно получить более удобное выражение для ![]() .
.
![]() (4.37)
(4.37)
Здесь, как и выше, амплитуда ![]() нормирует ожидаемый выход согласованного фильтра. Используя уравнение (3.11), можно записать следующее.
нормирует ожидаемый выход согласованного фильтра. Используя уравнение (3.11), можно записать следующее.
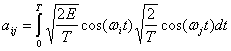 (4.38)
(4.38)
Следовательно,
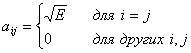 (4.39)
(4.39)
Другими словами, i-й вектор сигнала-прототипа расположен на i-й координатной оси на расстоянии ![]() от начала координат сигнального пространства. В этой схеме, при данном числе уровней М и данной Е, расстояние между любыми двумя векторами сигналов прототипов si и sj является постоянным.
от начала координат сигнального пространства. В этой схеме, при данном числе уровней М и данной Е, расстояние между любыми двумя векторами сигналов прототипов si и sj является постоянным.
![]() (4.40)
(4.40)
На рис. 4.14 показаны векторы сигналов-прототипов и области решений для троичной (М = 3) ортогональной модуляции FSK с когерентным обнаружением. Как правило, естественным выбором размера М сигнального множества является степень двойки. Причина неортодоксального выбора М = 3 состоит в том, что мы желаем исследовать сигнальное множество, большее чем бинарное, а визуальное представление сигнального пространства лучше всего выглядит при использовании взаимно перпендикулярных осей. Наибольшим числом перпендикулярных осей, которые можно аккуратно изобразить визуально, является 3. Как и при использовании модуляции PSK, сигнальное пространство разбивается на М различных областей, каждая из которых содержит один вектор сигнала-прототипа; в нашем примере, где области решений являются трехмерными, границы областей являются уже не линиями, а плоскостями. Оптимальное правило принятия решения состоит в следующем: определить сигнал к тому классу, индекс которого соответствует области нахождения принятого сигнала. На рис! 4.14 вектор принятого сигнала г изображен в области 2. Согласно приведенному выше правилу принятия решений, детектор классифицирует г как сигнал s2. Поскольку шум изображается гауссовым случайным вектором, существует отличная от нуля вероятность того, что вектор г даст сигнал, отличный от s2. Например, если передатчик послал сигнал s2, вектор г будет суммой сигнала и шума ![]() , а решение о выборе s2 будет справедливым; в то же время, если передатчик в действительности послал сигнал s2, вектор г будет суммой сигнала и шума
, а решение о выборе s2 будет справедливым; в то же время, если передатчик в действительности послал сигнал s2, вектор г будет суммой сигнала и шума ![]() , а решение относительно выбора s2 будет ошибочным. Вопросы вероятности возникновения ошибки при когерентном обнаружении сигналов в модуляции FSK подробно рассмотрены в разделе 4.7.3.
, а решение относительно выбора s2 будет ошибочным. Вопросы вероятности возникновения ошибки при когерентном обнаружении сигналов в модуляции FSK подробно рассмотрены в разделе 4.7.3.
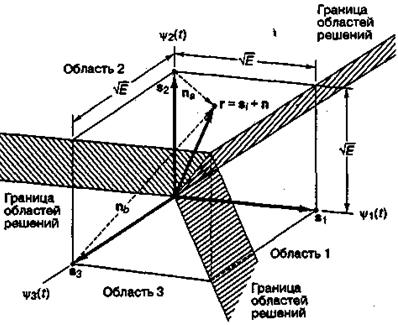
Рис. 4.14. Разбиение сигнального пространства для троичного пространства FSK
Пример 4.2. Принятая фаза как функция задержки распространения
а) Из схемы, приведенной на рис. 4.8, непонятно, откуда берутся опорные сигналы коррелятора. Кто-то может подумать, что они известны всегда и хранятся в памяти, пока не понадобятся. При некоторых обстоятельствах приемник действительно может, в разумных пределах, предсказывать некоторое ожидаемое значение амплитуды поступающего сигнала или его частоты. Но существует один параметр, который нельзя оценить без специальной помощи, — это фаза принятого сигнала. Наиболее популярным способом получения оценки фазы является использование схемы, называемой контурам фазовой автоподстройки частоты (ФАПЧ, phase-locked loop — PLL). Схема восстановления несущей захватывает прибывающую несущую волну (или воссоздает ее) и оценивает ее фазу. Чтобы показать, как иногда нереально предсказать фазу без использования ФАПЧ, рассмотрим канал радиосвязи, изображенный на рис. 4,15. Здесь мобильный пользователь расположен в точке А на расстоянии d от центральной станции, а задержка распространения сигнала равна Td. Используя комплексную форму записи, можем описать сигнал, излучаемый передатчиком, как ![]() , Пусть частота fо равна 1 ГГц. Если пренебречь шумом, сигнал, принятый центральной станцией, можно записать как
, Пусть частота fо равна 1 ГГц. Если пренебречь шумом, сигнал, принятый центральной станцией, можно записать как ![]() . Определите, на какое минимальное расстояние d (рис. 4.15) должен переместиться мобильный пользователь, чтобы это привело к изменению фазы принятого сигнала на 2л.
. Определите, на какое минимальное расстояние d (рис. 4.15) должен переместиться мобильный пользователь, чтобы это привело к изменению фазы принятого сигнала на 2л.
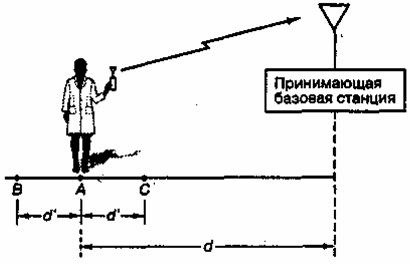
Рис. 4.15. Канал радиосвязи
б) Действительно ли нас волнует изменение фазы на 2π? Разумеется, нет, поскольку в этом случае вектор принятого сигнала будет находиться в той же точке, что и ранее, когда пользователь находился в точке А. Но зададимся вопросом, чему равно минимальное расстояние, изменяющее фазу на ![]() π/2 (скажем, дающее запаздывание на π/2)? Приемник должен отнести вектор, соответствующий r(t), к той же группе, что и в п. а, но запаздывание приводит к тому, что принятый сигнал уже имеет вид
π/2 (скажем, дающее запаздывание на π/2)? Приемник должен отнести вектор, соответствующий r(t), к той же группе, что и в п. а, но запаздывание приводит к тому, что принятый сигнал уже имеет вид ![]() , и коррелятор, используемый в процессе обнаружения, дает нулевой выход.
, и коррелятор, используемый в процессе обнаружения, дает нулевой выход.
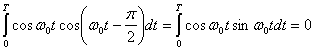
Определите минимальное расстояние перемещения пользователя, приводящее к изменению фазы на π/2.
Решение
а) Пусть в начальный момент времени t — 0 мобильный пользователь находится в точке А, так что вектор, принятый центральной станцией, дается выражением ![]() . Затем, после перемещения пользователя в точку В, принятый (еще сильнее запаздывающий) вектор
. Затем, после перемещения пользователя в точку В, принятый (еще сильнее запаздывающий) вектор ![]() можно записать в виде
можно записать в виде ![]() . Минимальное время задержки
. Минимальное время задержки ![]() , соответствующее повороту вектора на 2π, равно
, соответствующее повороту вектора на 2π, равно ![]() секунд. Следовательно, минимальное расстояние для такого поворота (предполагая идеальное электромагнитное распространение со скоростью света) равно следующему.
секунд. Следовательно, минимальное расстояние для такого поворота (предполагая идеальное электромагнитное распространение со скоростью света) равно следующему.
![]()
б) Используя предыдущий результат, получаем следующее расстояние для поворота вектора на π/2.
![]()
Очевидно, что даже если передатчик и приемник жестко установлены на стационарных башнях, небольшое смещение, вызванное ветром, может привести к абсолютной неопределенности относительно значения фазы. Если предположить, что используемая частота равна не 1 ГГц, а 10 ГГц, то минимальное расстояние изменяется с 7,5 см до 0,75 см. На практике зачастую желательно избегать приемников, использующих ФАПЧ. Вычисления, выполненные в данном примере, могут породить вопрос, как изменится вероятность ошибки, если в процессе обнаружения не будет использоваться информация о фазе? Другими словами, чем заплатит система, если обнаружение будет выполнено некогерентно? Этот и другие подобные вопросы рассматриваются в следующем разделе.

