Задача нахождения начальных постоянных напряжений и токов на внешних зажимах нелинейных полупроводниковых или электронных приборов, входящих в электрическую цепь, сводится к задаче анализа режима постоянного тока в исследуемой цепи, т. е., к анализу нелинейной резистивной цепи с источниками постоянного напряжения или (и) тока. Решаются подобные задачи обычно с использованием графических построений.

Ниже рассматривается задача анализа режима постоянного тока в электрической цепи с одним нелинейным двухполюсником, – нелинейным резистивным элементом (НЭ). Его ВАХ считается известной и заданной графически.

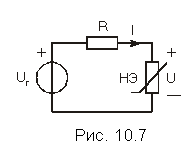
Рассмотрим простейшую электрическую цепь, изображенную на рис. 10.7. В нее входят источник постоянного напряжения с задающим напряжением U_г, линейный резистивный элемент R и нелинейный резистивный элемент, в котором подлежат определению постоянные напряжение U =U₀ и ток I = I₀. Рассмотрим два случая НЭ: с однозначной и многозначной ВАХ.

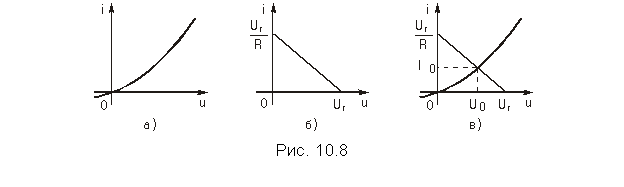
Нелинейный резистивный элемент с однозначной характеристикой

Пусть однозначная ВАХ нелинейного резистивного элемента имеет вид, показанный на рис. 10.8, а.

Согласно ЗНК (рис. 10.7) напряжение U = U_г—RI, и ток в элементе R связан с напряжением U на зажимах НЭ зависимостью I = (U_г—U)/R, представляющей собой прямую, проходящую через точки U_г на оси абсцисс и U_г/R – на оси ординат. Поскольку нелинейный и линейный элементы соединены последовательно, то ВАХ НЭ и прямая I = (U_г—U)/R, определяющие один и тот же ток, удовлетворяются одновременно, чему на графиках рис. 10.8, в соответствует точка их пересечения. Она и определяет искомые значения постоянных напряжения U₀ и тока I₀ в нелинейном резисторе, или, как принято говорить, его рабочую точку.

Графические построения, связанные с решением задачи, всегда выполнимы, а найденное ее решение – единственное.

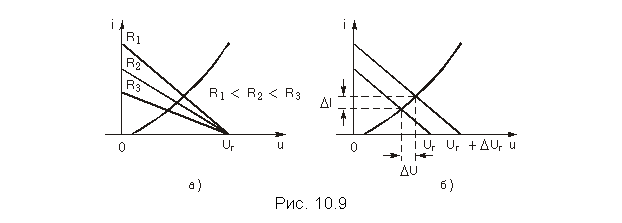
Рабочая точка нелинейного резистора изменяется как с изменением сопротивления R, так и с изменением задающего напряжения источника U_г. Изменение сопротивления R приводит к изменению наклона зависимости I = (U_г—U)/R и смещению рабочей точки на вольт-амперной характеристике нелинейного резистора (см. рис. 10.9, а). Изменение задающего напряжения на величину DU_г вызывает перемещение той же зависимости параллельно самой себе и изменение тока и напряжения в нелинейном резисторе соответственно на величины DI и DU (см. рис. 10.9, б).

Напомним, что отношение бесконечно малого приращения тока к бесконечно малому приращению напряжения на нелинейном элементе, обусловленных смещением рабочей точки, называется дифференциальной проводимостью (крутизной), а обратное отношение – дифференциальным сопротивлением нелинейного резистора в его рабочей точке.

Отношение постоянных тока и напряжения в рабочей точке нелинейного резистора определяет его статистическую проводимость, а обратное отношение – статическое сопротивление резистора в его рабочей точке.

Статическая проводимость пассивного нелинейного резистора всегда положительна. Положительна и дифференциальная проводимость нелинейного резистора с однозначной вольт-амперной характеристикой в силу возрастающего характера последней. Заметим также, что статическая и дифференциальная проводимости линейного резистора не отличаются одна от другой.

Нелинейный резистивный элемент с многозначной характеристикой

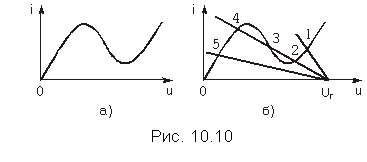
Пусть многозначная ВАХ нелинейного резистивного элемента в схеме рис. 10.7 имеет вид, показанный на рис. 10.10, а. Это характеристика туннельного диода. Для нахождения рабочей точки на ВАХ резистивного НЭ применим те же, что и выше, графические построения.

На рис. 10.10, б совмещены графики вольт-амперной характеристики нелинейного резистора и зависимостей I = (U_г—U)/R для трех различных значений сопротивления линейного резистора R и одного и того же значения напряжения задающего источника U_г.

Анализ рис. 10.10, б показывает, что рабочими точками могут быть точки 1 и 5, соответствующие единственному решению уравнений I = F(U) и I = (U_г—U)/R. Рабочими точками могут быть также точка 2 или точка 4. Точка 3, расположенная па ниспадающем участке ВАХ, является точкой неустойчивого равновесия. Можно показать, что если зафиксировать сопротивление R, при котором могут существовать три точки пересечения указанных зависимостей, и увеличивать задающее напряжение источника от нуля до величины U_г, то рабочей будет точка 4. Если же задающее напряжение источника от очень большого значения уменьшать до значения U_г, то рабочей будет точка 2.

Итак, в цепи с нелинейным двухполюсником, имеющим многозначную ВАХ задачи нахождения рабочей точки не всегда имеет единственное решение.

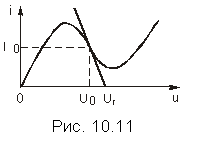
Рабочая точка может быть расположена и на ниспадающем участке вольт-амперной характеристики, если выбрать сопротивление R и задающее напряжение U_г так, как показано на рис. 10.11. Заметим, что в рабочей точке, расположенной на ниспадающем участке вольт-амперной характеристики, дифференциальная проводимость и дифференциальное сопротивление нелинейного резистора отрицательны, поскольку малым положительным значениям приращения напряжения (тока) на зажимах нелинейного резистора соответствуют отрицательные значения приращения тока (напряжения).

Метод эквивалентного генератора

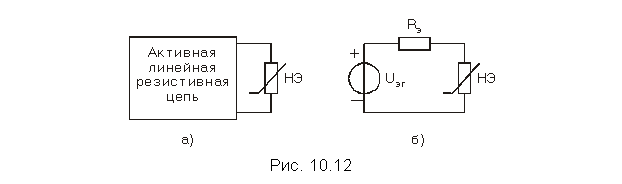
Изложенная методика определения рабочей точки в цепи с одним линейным и одним нелинейным резистивными элементами распространяется на резистивные цепи с одним резистивным НЭ и произвольным числом линейных резистивных элементов и источников постоянного напряжения или (и) тока, если воспользоваться теоремой об эквивалентном генераторе. Для этого следует внешнюю по отношению к нелинейному двухполюснику линейную активную цепь (см. рис. 10.12, а) заменить эквивалентным генератором с задающим напряжением U_эг и внутренним линейным резистивным эквивалентным сопротивлением R_э (рис. 10.12, б). Тогда схема анализируемой цепи не будет отличаться от схемы рис. 10.7, и задача нахождения рабочей точки сводится к рассмотренной выше.

Напряжения и токи в элементах цепи, внешней по отношению к НЭ, можно найти, воспользовавшись теоремой замещения. Для этого нелинейный резистивный элемент следует заменить источником напряжения (источником тока), напряжение (ток) которого равно (равен) найденному значению напряжения (тока) в рабочей точке. Напряжения и токи в линейной части электрической цепи находят любым методом анализа режима постоянного тока.

Метод, с использованием эквивалентного генератора, является графоаналитическим, поскольку в нем аналитические методы определения параметров эквивалентного генератора и расчета линейной цепи после замены НЭ источником напряжения или тока сочетаются с графическим методом нахождения рабочей точки.

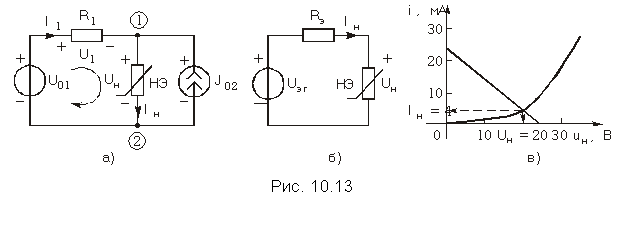
Пример. Применим метод эквивалентного генератора к схеме рис. 10.13, а, где U₀₁ = 14 В, J₀₂ = 10 мА, R₁ = 1 кОм, I_н = 10^–5U_н². Из рисунка следует, что напряжение U_эг при отключении НЭ равно

а эквивалентное сопротивление R_э = R₁ = 1 кОм. В соответствии с ЗНК (рис. 10.13, б) имеем

Построение графиков прямой линии и ВАХ нелинейного элемента показано на рис. 10.13, в. Пересечение этих кривых дает координаты рабочей точки: I_н = 4 мА и U_н = 20 В.