3.1. Дискретно-аналоговое представление регулярными выборками
3.2. Физическая трактовка процессов интерполяции сигналов
3.3. Задачи идеальной интерполяции
3.1. Дискретно-аналоговое представление регулярными выборками
При дискретно-аналоговом представлении сообщение на интервале времени T описывается вектором ![]()
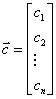 , (3.1)
, (3.1)
где ![]() - координаты.
- координаты.
Если шкала каждой координаты непрерывная, то это представление называется дискретно-аналоговым, а если шкала квантованная, то представление дискретно-квантованное, т.е. цифровое.
Дискретно-аналоговое представление сообщений может быть реализовано различными способами в зависимости от выбора системы координат. Наибольшее применение в РСПИ получили представления, у которых в качестве координат ![]() сообщения используется текущее значение сигнала в фиксированные моменты времени.
сообщения используется текущее значение сигнала в фиксированные моменты времени.
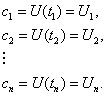 (3.2)
(3.2)
Координаты ![]() называются выборками или отсчетами, а моменты времени
называются выборками или отсчетами, а моменты времени ![]() - точками опроса.
- точками опроса.
При представлении регулярными выборками расстояние между соседними точками опроса одинаково и равно ![]() .
.
![]() , (3.3)
, (3.3)
где ![]() - период опроса,
- период опроса, ![]() - частота опроса.
- частота опроса.
Частота опроса ![]() является важнейшим параметром, который надо выбирать при представлении сообщения регулярными выборками.
является важнейшим параметром, который надо выбирать при представлении сообщения регулярными выборками.
Процесс формирования выборок в этом случае изображен на рисунке 3.1:
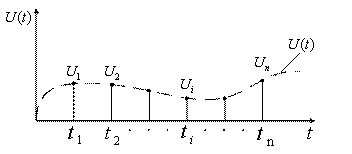
Рисунок 3.1
Выбор частоты опроса ![]() зависит от способа восстановления исходного сообщения на приемном конце. Восстановление непрерывной функции по её выборкам называется интерполяцией.
зависит от способа восстановления исходного сообщения на приемном конце. Восстановление непрерывной функции по её выборкам называется интерполяцией.
Рассмотрим случай, когда потребителю необходимо восстановить на приёмной стороне функцию![]() . Реально при восстановлении функции
. Реально при восстановлении функции ![]() может быть получена только её оценка
может быть получена только её оценка ![]() . Для доказательства этого утверждения представим интерполяционную обработку в следующем виде:
. Для доказательства этого утверждения представим интерполяционную обработку в следующем виде:
![]()
![]() , (3.4)
, (3.4)
где ![]() - интерполирующая (восстанавливающая, синтезирующая) функция. Функция
- интерполирующая (восстанавливающая, синтезирующая) функция. Функция
![]() , (3.5)
, (3.5)
т.е. ![]() есть функция с началом отсчета в точке мер выборки первичного сигнала. Суммирование в выражении (3.4) ведется по всем выборкам, участвующим в обработке. Определение вида функции
есть функция с началом отсчета в точке мер выборки первичного сигнала. Суммирование в выражении (3.4) ведется по всем выборкам, участвующим в обработке. Определение вида функции ![]() составляет сущность задачи выбора способа интерполяционной обработки.
составляет сущность задачи выбора способа интерполяционной обработки.
На точность функции восстановления функции ![]() влияют следующие факторы:
влияют следующие факторы:
- шумы интерполяции;
- шумы радиолинии;
- погрешности системы.
В дальнейшем будем учитывать только ошибку за счет интерполяции. Т.е. выборки будут считаться точными, а шумы отсутствующими. Тогда выражение для оценки первичного сигнала будет иметь следующий вид:
![]() . (3.6)
. (3.6)
Ошибка интерполяционной обработки в этом случае равна:
![]() . (3.7)
. (3.7)
При этом оценка ![]() должна быть получена на некотором интервале интерполяции
должна быть получена на некотором интервале интерполяции ![]() с учетом выборок, расположенных на конечном интервале обработки
с учетом выборок, расположенных на конечном интервале обработки ![]() . Интервал обработки
. Интервал обработки ![]() должен последовательно перемещаться в пределах интервала наблюдения
должен последовательно перемещаться в пределах интервала наблюдения ![]() (рисунок 3.2).
(рисунок 3.2).
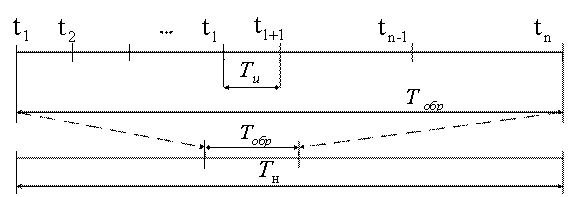
Рисунок 3.2
Таким образом, функция ![]() должна быть восстановлена для всех значений времени, лежащих внутри интервала интерполяции
должна быть восстановлена для всех значений времени, лежащих внутри интервала интерполяции ![]() , путем использования выборок в моменты времени
, путем использования выборок в моменты времени ![]() .
.![]() Это возможно потому, что существует корреляционная зависимость между значением первичного сигнала
Это возможно потому, что существует корреляционная зависимость между значением первичного сигнала ![]() , моментами времени
, моментами времени ![]() и
и ![]() . Интерполяция белого шума невозможна, т.к. его корреляционная функция есть дельта – функция.
. Интерполяция белого шума невозможна, т.к. его корреляционная функция есть дельта – функция.
Теоретически необходимо учитывать все отсчеты ![]() на интервале наблюдения
на интервале наблюдения ![]() , т.е. полагать
, т.е. полагать ![]() =
= ![]() . Но при этом результаты интерполяции могут быть получены спустя время
. Но при этом результаты интерполяции могут быть получены спустя время ![]() , и для реализации требуется устройство с большой памятью. С удалением точки опроса от интервала интерполяции
, и для реализации требуется устройство с большой памятью. С удалением точки опроса от интервала интерполяции ![]() уменьшаются корреляционные связи и их учет дает малый вклад в ошибку интерполяции. Поэтому имеют смысл учитывать только те отсчеты, выборки которых коррелированны с функцией
уменьшаются корреляционные связи и их учет дает малый вклад в ошибку интерполяции. Поэтому имеют смысл учитывать только те отсчеты, выборки которых коррелированны с функцией ![]() на интервале интерполяции
на интервале интерполяции ![]() , с коэффициентами корреляции К(τ) = 0.05 – 0.2. Конкретные значения К(τ) определяются требованиями к точности интерполяции.
, с коэффициентами корреляции К(τ) = 0.05 – 0.2. Конкретные значения К(τ) определяются требованиями к точности интерполяции.
3.2. Физическая трактовка процессов интерполяции сигналов
Основное математическое соотношение интерполяционной обработки:
![]() , (3.8)
, (3.8)
можно проиллюстрировать следующим образом (рисунок 3.3).
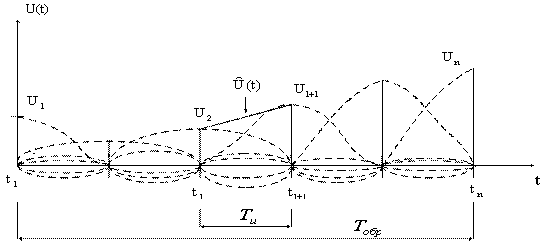
Рисунок 3.3
В качестве интерполяционной функции в этом примере используется функция ![]() . Интервалы интерполяции
. Интервалы интерполяции![]() и обработки
и обработки ![]() должны последовательно сдвигаться по времени. Операцию интерполяции можно выполнить с помощью линейного фильтра с импульсной характеристикой вида:
должны последовательно сдвигаться по времени. Операцию интерполяции можно выполнить с помощью линейного фильтра с импульсной характеристикой вида:
![]() . (3.9)
. (3.9)
Для доказательства этого утверждения обозначим сигнал на входе и выходе линейного фильтра через ![]() и
и ![]() (рисунок 3.4):
(рисунок 3.4):

Рисунок 3.4
Представим сигнал на входе линейного фильтра в виде последовательности кратковременных импульсов, площадь которых равна соответствующим выборкам
![]() . (3.10)
. (3.10)
Из свойств линейных систем следует, что сигнал на выходе равен:
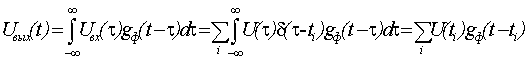 (3.11)
(3.11)
Выражение (3.11) получается с учетом фильтрующего свойства δ-функции. Если импульсная характеристика линейного фильтра ![]() удовлетворяет выражению (3.9), то соотношение (3.11) переходит в формулу для интерполяционной обработки:
удовлетворяет выражению (3.9), то соотношение (3.11) переходит в формулу для интерполяционной обработки:
![]() . (3.12)
. (3.12)
Идеальное восстановление функции на выходе линейного фильтра невозможно, т.к.:
- отклик на выходе линейного фильтра не может появиться раньше соответствующей выборки на входе;
- число выборок не равно бесконечности;
- АЧХ фильтра отличается от идеальной.
3.3. Задачи идеальной интерполяции
В общем случае формула интерполяции имеет вид:
![]() , (3.13)
, (3.13)
![]() - оценка значения i-ой выборки,
- оценка значения i-ой выборки, ![]() - восстановленный первичный сигнал,
- восстановленный первичный сигнал, ![]() .
.
Интерполяция возможна в том случае, если в сигнале имеются корреляционные связи. Может быть поставлена задача оптимального выбора вида функции ![]() , при которой ошибка интерполяции минимальна.
, при которой ошибка интерполяции минимальна.
Рассмотрим задачу идеальной интерполяции сигнала при предположении, что ![]() , т.е. отсутствуют внешние шумы и ошибки системы.
, т.е. отсутствуют внешние шумы и ошибки системы.
Пусть непрерывный первичный сигнал описывается корреляционной
функцией ![]() . Требуется определить форму интерполирующей функции, обеспечивающей при заданных значениях коэффициента корреляции минимум СКО
. Требуется определить форму интерполирующей функции, обеспечивающей при заданных значениях коэффициента корреляции минимум СКО
![]() . (3.14)
. (3.14)
Можно показать, что в этом случае оптимальная интерполирующая функция имеет вид:
![]() , (3.15)
, (3.15)
где ![]() - весовые коэффициенты, однозначно связанные со значениями коэффициентов корреляции в точках
- весовые коэффициенты, однозначно связанные со значениями коэффициентов корреляции в точках ![]() ,
, ![]() .
.
Т.о., оптимальная интерполирующая функция может быть определена как взвешенная сумма функций времени равных корреляционной функции первичного сигнала. Как следствие этой теории может бать доказана следующая теорема:
Если на интервале интерполяции ![]() корреляционная функция
корреляционная функция ![]() и ее взвешенная сумма хорошо аппроксимируются полиномом, то использование этого приближения обеспечит среднеквадратическое приближение близкое к идеальному. Т.е. требуется хорошая аппроксимация не всей корреляционной функции, а только ее части, приходящейся на интервал интерполяции (рисунок 3.5).
и ее взвешенная сумма хорошо аппроксимируются полиномом, то использование этого приближения обеспечит среднеквадратическое приближение близкое к идеальному. Т.е. требуется хорошая аппроксимация не всей корреляционной функции, а только ее части, приходящейся на интервал интерполяции (рисунок 3.5).
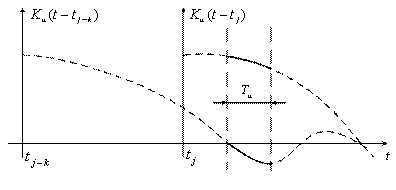
Рисунок 3.5
Чем меньше ![]() , тем точнее возможна аппроксимация в виде многочлена и тем проще могут быть аппроксимирующие полиномы. Проиллюстрируем эту теорему для сигнала с прямоугольным спектром (рисунок 3.6):
, тем точнее возможна аппроксимация в виде многочлена и тем проще могут быть аппроксимирующие полиномы. Проиллюстрируем эту теорему для сигнала с прямоугольным спектром (рисунок 3.6):
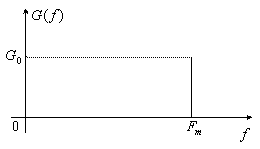
Рисунок 3.6
Известно, что в этом случае в соответствии с теоремой
В.А. Котельникова возможно разложение первичного сигнала в ряд:
![]() , (3.16)
, (3.16)
где ![]() - частота опроса. В точках
- частота опроса. В точках ![]()
![]() интерполирующая функция равна:
интерполирующая функция равна:
![]() . (3.17)
. (3.17)
Сопоставим этот результат с выражением для идеальной интерполирующей функции:
![]() . (3.18)
. (3.18)
Чтобы эти формулы совпали, необходимо чтобы при ![]() , а в случае
, а в случае ![]()
![]()
![]() , т. е. чтобы корреляционная функция имела вид:
, т. е. чтобы корреляционная функция имела вид:
![]() . (3.19)
. (3.19)
Такой функцией корреляции обладает сигнал с прямоугольным спектром, а условие ![]() при
при ![]() приводит к требованию, чтобы частота опроса
приводит к требованию, чтобы частота опроса ![]() .
.
Это соотношение не может быть использовано на практике по следующим причинам:![]()
1. Сигнала с идеальным прямоугольным спектром не существует.
2. Число выборок ![]() .
.
На практике при представлении регулярными выборками частота опроса выбирается исходя из соотношения
![]() æ
æ![]() , (3.20)
, (3.20)
где ![]() определяется формой спектра сигнала, а æ – коэффициент запаса, зависящий от вида интерполирующих полиномов и требуемых значений показателя верности.
определяется формой спектра сигнала, а æ – коэффициент запаса, зависящий от вида интерполирующих полиномов и требуемых значений показателя верности.
3.4. Интерполяция алгебраическими полиномами
Как было показано выше, для первичных сигналов с разными корреляционными функциями необходимо использовать разные интерполирующие функции. Такой подход не приемлем для практики, т.к. требует выполнения большого объема предварительных работ для определения вида интерполирующих функций. Для преодоления этих затруднений возможны два пути:
1. Использование для группы сигналов с близкими корреляционными функциями интерполирующей функции одного вида.
2. Применение в качестве интерполирующих функций хорошо программируемых функций с выбором частоты опроса, обеспечивающих во всех случаях требуемую верность.
Второй путь наиболее прост, но приводит к завышенным частотам опроса и, следовательно, к увеличению загрузки радиолинии. Наиболее рациональным является комбинированное использование обоих путей.
Во многих случаях в качестве интерполирующих путей используются алгебраические полиномы низких степеней, в частности полиномы Лагранжа. Интерполирующая функция по Лагранжу записывается в следующем виде:![]()
![]() (3.21)
(3.21)
где ![]() - символ произведения, в котором отсутствуют сомножители при
- символ произведения, в котором отсутствуют сомножители при ![]() . Нетрудно убедиться, что
. Нетрудно убедиться, что ![]() при
при ![]() и
и ![]() при
при ![]() .
.
При интерполяции по Лагранжу требуется определенным образом выбрать интервал обработки ![]() .
.
1) Число точек опроса n четное (рисунок 3.7).
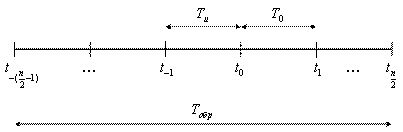
Рисунок 3.7
2) Число точек опроса n нечетное (рисунок 3.8).
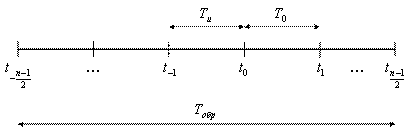
Рисунок 3.8
Запишем момент времени, в котором ищется интерполяционная оценка в виде
![]() , (3.22)
, (3.22)
где ![]() - точка отсчета,
- точка отсчета, ![]() - период опроса,
- период опроса, ![]() - безразмерное время, которое может непрерывно изменяться в пределах
- безразмерное время, которое может непрерывно изменяться в пределах
![]() , при
, при ![]() (3.23)
(3.23)
![]() , при
, при ![]() ,
, ![]() (3.24)
(3.24)
На практике интерполяция по Лагранжу используется при n = 1, 2, 3:
1. Ступенчатая интерполяция (полиномы нулевой степени ) (рисунок 3.9).
В этом случае n = 1 и для интерполяции используется лишь одна выборка
![]() ,
, ![]() ,
, ![]() и
и ![]() .
.
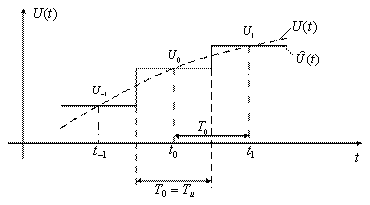
Рисунок 3.9
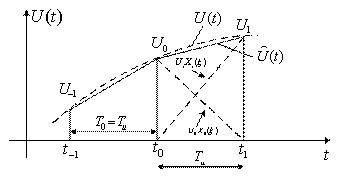
2. Линейная интерполяция (полиномы первой степени) (рисунок 3.10).
При этом ![]() ,
, ![]() ,
, ![]() и интерполирующие функции имеют вид
и интерполирующие функции имеют вид ![]() ,
, ![]() .
.![]()
![]()
![]()
![]()
Рисунок 3.10
3. Квадратичная интерполяция (квадратичная интерполяция) (рисунок 3.11).
При этом ![]() ,
, ![]() ,
, ![]() и интерполирующие функции имеют вид
и интерполирующие функции имеют вид ![]() ,
, ![]() ,
, ![]() .
.
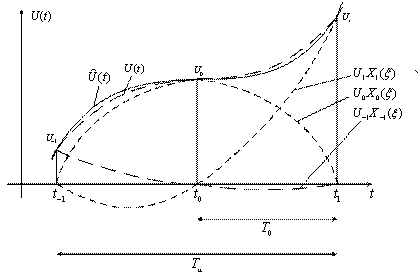
Рисунок 3.11
Можно показать, что верхние оценки относительных ошибок в этом случае равны ![]() ,
, ![]() ,
, ![]() ,
,
где ![]() - граничная частота спектра сигнала,
- граничная частота спектра сигнала, ![]() - частота опроса.
- частота опроса.
При ![]() и
и ![]() частота опроса
частота опроса ![]() ,
, ![]() ,
, ![]() .
.
При восстановлении функции по отсчетам обычно получается плавная кривая, поэтому, можно для практических расчетов выбрать частоту опроса по формуле ![]() .
.
3.5. Определение частоты опроса
Определим частоту опроса первичного сигнала при среднем квадратическом приближении алгебраическими полиномами. Используем показатель верности оценки ![]() в форме интегральной средней квадратической ошибки
в форме интегральной средней квадратической ошибки
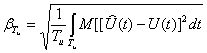 . (3.26)
. (3.26)
Более удобно использовать приведенный показатель верности:
![]() . (3.27)
. (3.27)
Применим эту формулу для определения частоты опроса четырех моделей первичного сигнала: Модель 1. Сигнал с ограниченным равномерным спектром (рисунок 3.12).
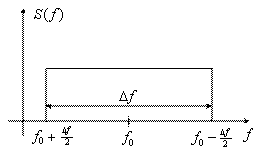
Рисунок 3.12
Применяя косинус преобразование Фурье от ![]() , получим функцию корреляции этого сигнала:
, получим функцию корреляции этого сигнала:
![]() . (3.28)
. (3.28)
Модель 2. Сигнал с треугольным спектром (рисунок 3.13).
![]() ,
, ![]() .
.
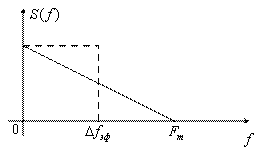
Рисунок 3.13
Эффективная ширина спектра в этом случае имеет вид ![]() , а функция корреляции равна
, а функция корреляции равна
![]() . (3.29)
. (3.29)
Модель 3. Сигнал марковского типа (рисунок 3.14).
Энергетический спектр этого сигнала описывается соотношением
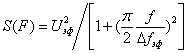 , а функция корреляции равна
, а функция корреляции равна
![]() . (3.30)
. (3.30)
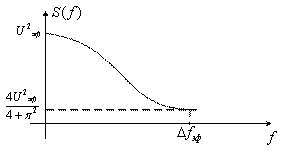
Рисунок 3.14
Модель 4. Сигнал с колокольным спектром (рисунок 3.15). Энергетический спектр этого сигнала описывается соотношением
![]() ,
,
где ![]() , а функция корреляции равна
, а функция корреляции равна
![]() . (3.31)
. (3.31)
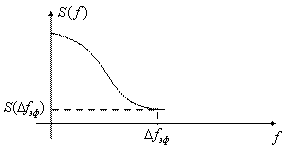
Рисунок 3.15
Эти модели охватывают значительную часть практически используемых сигналов и являются стационарными случайными процессами. Применяя для этих моделей интерполяцию по Лагранжу при ![]() получим следующие формулы (таблица 3.1) для расчета величины æ =
получим следующие формулы (таблица 3.1) для расчета величины æ = ![]() .
.
В случае модели 1 и идеальной интерполяции, т.е. при опросе по В.А. Котельникову, æ = 1. Формулы, приведенные в таблице используются для определения частоты опроса ![]() = æ
= æ![]() .
.
Таблица 3.1
| Модель | æ = |
||
|
1 |
n = 1 |
n = 2 |
n = 3 |
|
|
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
Построим графики зависимости æ от показателя верности ![]() для различных моделей сигналов (рисунки 3.16, 3.17).
для различных моделей сигналов (рисунки 3.16, 3.17).
Выводы:
1. Для всех моделей, за исключением третьей, интерполяция полиномами более высокого порядка позволяет уменьшить частоту опроса при той же верности.
2. При переходе от линейной интерполяции к квадратичной, уменьшение частоты опроса ![]() не столь значительно, как при переходе от ступенчатой интерполяции к линейной.
не столь значительно, как при переходе от ступенчатой интерполяции к линейной.
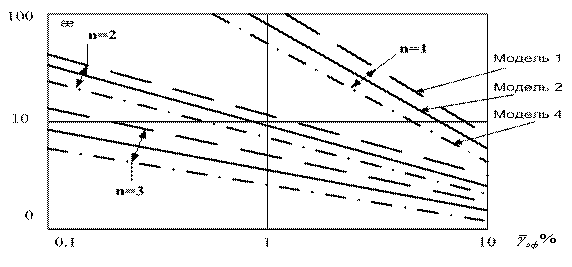
Рисунок 3.16
![]()
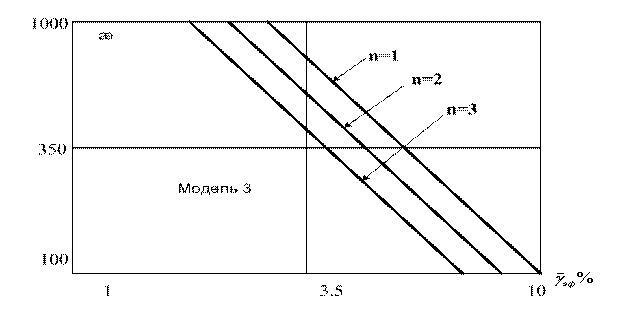
Рисунок 3.17
3. Увеличивать степень полинома целесообразно только при увеличении требований к точности интерполяции.
4. Для третьей модели переход от линейной модуляции к квадратичной нецелесообразен, что объясняется свойствами марковских сигналов.
5. При интерполяции алгебраическими полиномами первичного сигнала коэффициент корреляции между соседними выборками равен 0,85 – 0,995. Это приводит к неэффективному использованию пропускной способности канала передачи информации.
6. Для определения частоты опроса необходимо располагать:
- спектральными характеристиками первичного сигнала, т.е. полосой
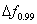 по уровню 0,99 энергии сигнала;
по уровню 0,99 энергии сигнала; - точностными характеристиками, т.е. показателем верности
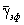 %;
%; - задать алгоритм обработки, т.е. тип интерполирующего полинома.

