1.2.1. Детерминированные и случайные сигналы
1.2.2. Периодические и непериодические сигналы
1.2.3. Аналоговые и дискретные сигналы
1.2.1. Детерминированные и случайные сигналы
Сигнал можно классифицировать как детерминированный (при отсутствии неопределенности относительно его значения в любой момент времени) или случайный, в противном случае. Детерминированные сигналы моделируются математическим выражением 
. Для случайного сигнала такое выражение написать невозможно. Впрочем, при наблюдении случайного сигнала (также называемого случайным процессом) в течение достаточно длительного периода времени, могут отмечаться некоторые закономерности, которые можно описать через вероятности и среднее статистическое. Такая модель, в форме вероятностного описания случайного процесса, особенно полезна для описания характеристик сигналов и шумов в системах связи.
1.2.2. Периодические и непериодические сигналы
Сигнал 
называется периодическим во времени, если существует постоянное 
, такое, что
для 
(1.2)
где через t обозначено время. Наименьшее значение 
, удовлетворяющее это условие, называется периодом сигнала . Период определяет длительность одного полного цикла функции . Сигнал, для которого не существует значения , удовлетворяющего уравнение (1.2), именуется непериодическим.
1.2.3. Аналоговые и дискретные сигналы
Аналоговый сигнал является непрерывной функцией времени, т.е. однозначно определяется для всех t. Электрический аналоговый сигнал возникает тогда, когда физический сигнал (например, речь) некоторым устройством преобразовывается в электрический. Для сравнения, дискретный сигнал 
является сигналом, существующим в дискретные промежутки времени; он характеризуется последовательностью чисел, определенных для каждого момента времени, кТ, где k - целое число, а Т - фиксированный промежуток времени.
1.2.4. Сигналы, выраженные через энергию или мощность
Электрический сигнал можно представить как изменение напряжения 
или тока 
с мгновенной мощностью 
, подаваемой на сопротивление R:
(1.3,а)
или
(1.3.,б)
В системах связи мощность часто нормируется (предполагается, что сопротивление R равно 1 Ом, хотя в реальном канале оно может быть любым). Если требуется определить действительное значение мощности, оно получается путем «денормирования» нормированного значения. В нормированном случае уравнения (1.3,а) и (1.3,6) имеют одинаковый вид. Следовательно, вне зависимости от того, представлен сигнал через напряжение или ток, нормированная форма позволяет нам выразить мгновенную мощность как
, (1.4)
где - это либо напряжение, либо ток. Рассеивание энергии в течение промежутка времени (
) реального сигнала с мгновенной мощностью, полученной с помощью уравнения (1.4), может быть записано следующим образом.
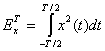(1.5)
Средняя мощность, рассеиваемая сигналом в течение этого интервала, равна следующему.
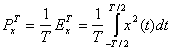(1.6)
Производительность системы связи зависит от энергии принятого сигнала; сигналы с более высокой энергией обнаруживаются более достоверно (с меньшим числом ошибок) - работу по обнаружению выполняет принятая энергия. С другой стороны, мощность - это скорость поступления энергии. Этот момент важен по нескольким причинам. Мощность определяет напряжение, которое необходимо подать на передатчик, и напряженность электромагнитных полей, которые следует учитывать в радиосистемах (т.е. поля в волноводах, соединяющих передатчик с антенной, и поля вокруг излучающих элементов антенны).
При анализе сигналов связи зачастую желательно работать с энергией сигнала. Будем называть энергетическим сигналом тогда и только тогда, когда он в любой момент времени имеет ненулевую конечную энергию (
), где
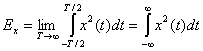(1.7)
В реальной ситуации мы всегда передаем сигналы с конечной энергией (). Впрочем, для описания периодических сигналов, которые по определению (уравнение (1.2)) существуют всегда и, следовательно, имеют бесконечную энергию, и для работы со случайными сигналами, также имеющими неограниченную энергию, удобно определить класс сигналов, выражаемых через мощность. Итак, сигнал удобно представить с использованием мощности, если он является периодическим и в любой момент времени имеет ненулевую конечную мощность (
), где
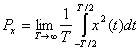(1.8)
Определенный сигнал можно отнести либо к энергетическому, либо периодическому. Энергетический сигнал имеет конечную энергию, но нулевую среднюю мощность, тогда как периодический сигнал имеет нулевую среднюю мощность, но бесконечную энергию. Сигнал в системе может выражаться либо через его энергетические, либо периодические значения. Общее правило: периодические и случайные сигналы выражаются через мощность, а сигналы, являющиеся детерминированными и непериодическими, - через энергию [1, 2].
Энергия и мощность сигнала - это два важных параметра в описании системы связи. Классификация сигнала либо как энергетического, либо как периодического является удобной моделью, облегчающей математическую трактовку различных сигналов и шумов. В разделе 3.1.5 эти идеи развиваются в контексте цифровых систем связи.
1.2.5. Единичная импульсная функция
Полезной функцией в теории связи является единичный импульс, или дельта-функция Дирака 
. Импульсная функция - это абстракция, импульс с бесконечно большой амплитудой, нулевой шириной и единичным весом (площадью под импульсом), сконцентрированный в точке, в которой значение его аргумента равно нулю. Единичный импульс задается следующими соотношениями.
(1.9)
для 
(1.10)
не ограничена в точке 
(1.11)
(1.12)
Единичный импульс - это не функция в привычном смысле этого слова. Если входит в какую-либо операцию, его удобно считать импульсом конечной амплитуды, единичной площади и ненулевой длительности, после чего нужно рассмотреть предел при стремлении длительности импульса к нулю. Графически 
можно изобразить как пик, расположенный в точке 
, высота которого равна интегралу от него или его площади. Таким образом, 
с постоянной А представляет импульсную функцию, площадь которой (или вес) равна А, а значение везде нулевое, за исключением точки .
Уравнение (1.12) известно как просеивающее (или квантующее) свойство единичной импульсной функции; интеграл от единичного импульса и произвольной функции дает выборку функции в точке .