Определим вероятность ошибки в системе передачи двоичных сигналов при приеме на оптимальный приемник. Эта вероятность, очевидно, будет минимально возможной и будет характеризовать потенциальную, помехоустойчивость при данном способе передачи. При приеме на реальный приемник помехоустойчивость может быть равна потенциальной, но не может быть больше ее.

Пусть сигнал принимает значения s(t) с вероятностью Ри значения s(t) с вероятностью . Если передавался сигнал s то согласно условию (5.31) ошибка произойдет в том случае, когда

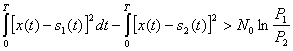(5.39)

Так как x(t) = s1(t)+w(t), то неравенство (5.39) может быть приведено к виду

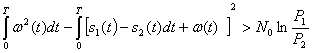
или

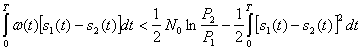(5.40)

В соответствии с выражениями (5.18) и (5.19) левую, часть неравенства (5.40) можно записать в следующем виде:

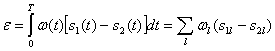(5.41)

Так как каждый коэффициент имеет нормальное распределение со средним значением, равным нулю, то сумма (5.41) будет также представлять собой нормальную случайную величину с нулевым средним значением и дисперсией

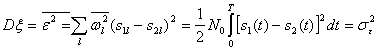(5.42)

Плотность вероятности случайной величины |

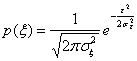
Согласно (5.40) ошибка произойдет при передаче сигнала -s, если

Величина этой ошибки будет равна:

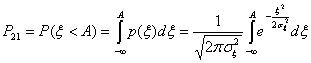(5,43)

Вводя новую переменную на основании соотношения (2.29) имеем

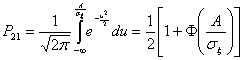
где

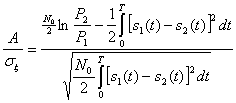
После несложных преобразований окончательно получаем

(5.44)

где

(5.45)

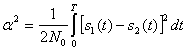(5.46)

Совершенно аналогично определяется вероятность ошибки при передаче сигнала s(t):

(5.47)

где

(5.48)

Полная вероятность ошибки при оптимальном приеме бинарных. сигналов s(t) и s(t) будет равна:

(5,49)

или согласно (5.44) и (5.47)

(5.50)

Из полученных формул следует, что вероятность ошибки, определяющая потенциальную помехоустойчивость, зависит от двух величин: ² и P/P. Первая величина определяется отношением удельной энергии разности сигналов к интенсивности помехи N. Чем больше это отношение, тем больше потенциальная помехоустойчивость. Отношение априорных вероятностей P/P определяется статистическими свойствами передаваемых сообщений.

Если передаваемые сигналы равновероятны P=P=0,5, то ф-ла (5.50) упрощается и принимает вид

(5.51)

Формулу (5.51) легко получить из геометрических представлений. Как это видно из рис. 5.3, при передаче сигнала s1 ошибка произойдет в том случае, если будет выполняться неравенство r>r2

или . Следовательно, вероятность ошибки можно определить как вероятность выполнения одного из этих неравенств, т. е.

Умножив обе части неравенства на d, получаем

где =— случайная величина (5.41), имеющая нормальное распределение с дисперсией (5.42). Тогда на основании (2.32) имеем

где

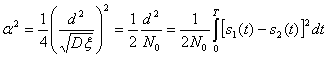
что совпадает с (5.51) и (5.46).

При малой интенсивности помех, когда , в ф-лах (5.45) и (5.48) вторым членом можно пренебречь. В этом случае ф-ла (5.50) также приводится к ф-ле (5.51). Вероятность ошибки при этом практически не зависит от Pи Р2. при большом уровне помех, когда мало, зависимость вероятности ошибки от отношения априорных вероятностей P/ Р2 становится заметной. С увеличением этого отношения вероятность ошибки увеличивается [4].

Таким образом, при равновероятных сигналах вероятность ошибки полностью определяется величиной . Значение этой величины зависит от спектральной плотности помех N0 и передаваемых сигналов s(t) и s(t).

Для систем с активной паузой, в которых сигналы имеют одинаковую энергию , выражение для ² можно представить в следующем виде:

(5.52)

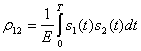— коэффициент взаимной корреляции

между сигналами, — отношение энергии сигнала к удельной мощности помехи.

Вероятность ошибки для таких систем определяется формулой

(5.53)

Отсюда следует, что при , т. е. , система обеспечивает наибольшую потенциальную помехоустойчивость. Эта система с противоположными сигналами. Для нее - Практической реализацией системы с противоположными сигналами является система с фазовой манипуляцией.

Сравнение различных систем передачи дискретных сообщений удобно производить по параметру ², представляющему собой приведенное отношение сигнала к помехе на выходе оптимального приемника при заданном способе передачи , или по величине выигрыша

(5.54)

где . Множитель TF определяет выигрыш за счет оптимальной обработки сигнала на приеме, а (1 —) — за счет способа передачи.

В общем виде радиотелеграфный сигнал можно записать

(5.55)

где параметры колебания принимают определенные значения в зависимости от вида манипуляции. Согласно (5.46) для сигналов (5.55) имеем:

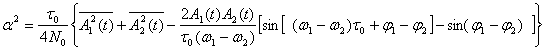(5.56)

Для амплитудной манипуляции A(t)=A0, A2(t)=0

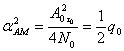
2 -

Для частотной манипуляции A(t)=A2(t)=A0. При оптимальном выборе разноса частот (), где k— целое

число и Тогда на основании (5.56) получаем

Для фазовой манипуляции A(t)=A2t)=A0, ,

Сравнение полученных формул показывает, что из всех систем передачи бинарных сигналов наибольшую потенциальную помехоустойчивость обеспечивает система с фазовой манипуляцией. По сравнению с ЧМ она позволяет получить двукратный, а по сравнению с AM — четырехкратный выигрыш по мощности.

В системах связи сигнал обычно, составляется из последовательности простых сигналов. Так, в телеграфии каждой букве соответствует кодовая комбинация, состоящая из даты элементарных посылок. Возможны и более сложные комбинации. Если элементарные сигналы, составляющие кодовую комбинацию, независимы, то вероятность ошибочного приема кодовой комбинации определяется следующей формулой:

(5.57)

где — вероятность ошибки элементарного сигнала, п — число элементарных сигналов в кодовой комбинации (значность кода).

Следует заметить, что вероятность ошибки в рассмотренных выше случаях полностью определяется отношением энергии сигнала к спектральной плотности помехи и не зависит от формы сигнала. В общем случае, когда спектр помехи отличается от равномерного, вероятность ошибки можно уменьшить, изменяя спектр сигнала, т. е. его форму.