14.1.1. Модель процесса шифрования и дешифрования

14.1.2. Задачи системы шифрования

14.1.3. Классические угрозы

14.1.4. Классические шифры

14.1.1. Модель процесса шифрования и дешифрования

Желание общаться конфиденциально уходит своими корнями в далекое прошлое. История секретного общения богата уникальными изобретениями и красочными анекдотами [1]. Изучение путей передачи сообщений, которые не допускали бы постороннего вмешательства, называется криптографией. Термины шифрование и кодирование обозначают преобразования сообщений, выполняемые передатчиком, а термины дешифрование и декодирование — обратные преобразования, производимые приемником. Основными причинами использования криптосистем в общении являются (1) обеспечение конфиденциальности, т.е. предотвращение извлечения информации из канала посторонним лицом (подслушивание); (2) аутентификация, предотвращение внедрения в канал информации посторонними людьми (обманный доступ). Часто, как в случае электронной пересылки или договорных переговоров, важно обеспечить электронный эквивалент письменной подписи. Это необходимо для того, чтобы устранить какие-либо недоразумения между отправителем и получателем относительного того, какое сообщение было отправлено и было ли оно вообще отправлено.

На рис. 14.1 изображена модель криптографического канала. Сообщение, или открытый текст M, шифруется путем обратимого преобразования Ек, дающего шифрованный текст С=Ек(М). Шифрованный текст пропускается через незащищенный, или общедоступный канал. После получения шифрованного сообщения С, его исходное значение восстанавливается с помощью операции дешифрования, описываемой обратным преобразованием Dk = Ек^-1, что выглядит следующим образом.

(14.1)

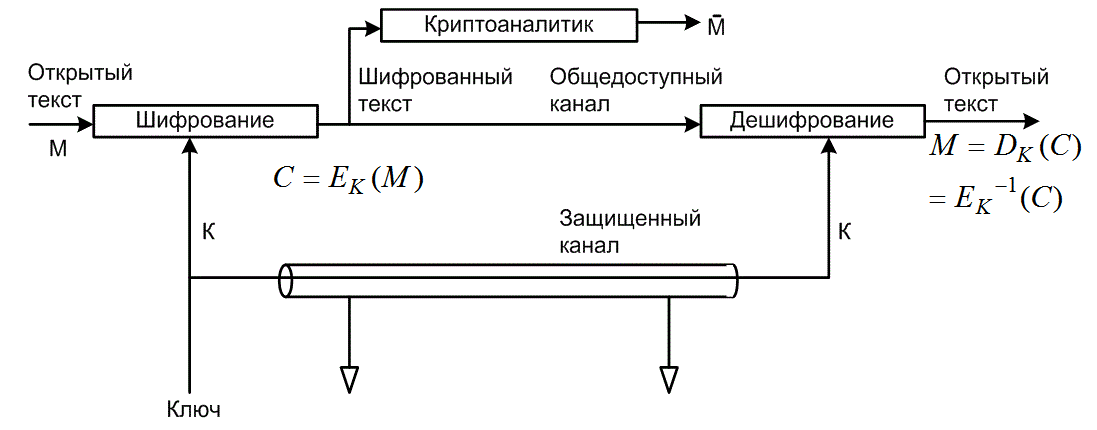Рис. 14.1. Модель криптографического канала

Параметром К обозначается множество символов или характеристик, называемых ключом, определяющим конкретное шифрующее преобразование Екиз семейства криптографических преобразований. Первоначально защищенность криптосистем зависела от секретности всего процесса шифрования, но в конечном итоге были разработаны системы, для которых общая природа преобразования шифрования или алгоритма могла быть общеизвестна, а секретность системы зависела от специального ключа. Ключ использовался для шифрования нешифрованного сообщения, а также для дешифрования шифрованного сообщения. Здесь можно отметить аналогию с универсальным компьютером и компьютерной программой. Компьютер, подобно криптосистеме, способен на множество преобразований, из которых компьютерная программа, подобно специальному ключу, выбирает одно. В большинстве криптосистем каждый, имеющий доступ к ключу, может как шифровать, так и дешифровать сообщения. Ключ передается разрешенным пользователям через секретный канал (в качестве примера может быть использован курьер для передачи из рук в руки важной ключевой информации); ключ, как правило, остается неизменным в течение значительного числа передач. Целью криптоаналитика (противника) является оценка открытого текста посредством анализа шифрованного текста, полученного из общедоступного канала, без использования ключа.

Схемы шифрования можно разбить на две основные категории: блочное и шифрование потока данных, или просто поточное. При блочном шифровании нешифрованный текст делится на блоки фиксированного размера, после чего каждый блок шифруется независимо. Следовательно, одинаковые блоки открытого текста с помощью данного ключа будут преобразовываться в одинаковые блоки шифрованного текста (подобно блочному кодированию). При поточном шифровании (подобном сверточному кодированию) блоков фиксированного размера не существует. Каждый бит открытого текста /и/ шифруется с помощью i-го элемента ki, последовательности символов (ключевого потока), генерируемой ключом. Процесс шифрования является периодическим, если ключевой поток начинает повторяться после р символов (причем р фиксированно); в противном случае он является непериодическим.

В общем случае схема шифрования существенно отличается от схемы канального кодирования. Например, при шифровании данные открытого текста не должны явно фигурировать в шифрованном тексте, а при канальном кодировании в систематической форме коды часто содержат неизмененные биты сообщения плюс биты четности (см. раздел 6.4.5). Существуют и другие отличия шифрования и канального кодирования. При блочном шифровании единственный бит ошибки на входе дешифратора может изменить значение многих выходных битов в блоке. Этот эффект, известный как накопление ошибки (error propagation), часто является желаемым криптографическим свойством, поскольку для несанкционированных пользователей он создает дополнительные сложности при расшифровке сообщений. В то же время при канальном кодировании такое свойство является нежелательным, поскольку хотелось бы, чтобы система исправила как можно больше ошибок и на выходную информацию входные ошибки относительно не влияли.

14.1.2. Задачи системы шифрования

Основные требования к системе шифрования можно сформулировать следующим образом.

1. Обеспечить простые и недорогие средства шифрования и дешифрования для разрешенных пользователей, обладающих соответствующим ключом.

2. Задачу криптоаналитика по производству оценки нешифрованного текста без помощи ключа сделать максимально сложной и дорогой.

Последовательно создаваемые криптосистемы делятся на безусловно защищенные или схемы, защищенные по вычислениям. Говорят, что система безусловно защищена, если информации, имеющейся у криптоаналитика, не достаточно для определения преобразований шифрования и дешифрования, независимо от того, какой вычислительной мощностью он располагает. Одна из таких систем, которая называется системой разового заполнения, включает шифрование сообщения с помощью случайного ключа, который применяется только один раз. Ключ никогда не используется повторно; следовательно, криптоаналитик не получает информации, которая может использоваться для расшифровки последующих передач, использующих тот же ключ. Хотя такая система является безусловно защищенной (см. раздел 14.2.1), в общепринятой системе связи она применяется редко, поскольку для каждого нового сообщения необходимо распространить новый ключ, а это обычно затруднительно. Вообще, распределение ключей разрешенным пользователям является основной проблемой при использовании любой криптосистемы, даже если ключ применяется в течение продолжительного периода времени. Хотя и можно доказать, что некоторые системы являются безусловно защищенными, общей схемы доказательства защищенности произвольной криптосистемы в настоящее время не существует. Таким образом, в спецификациях большинства криптосистем формально указывается, что они защищены по вычислениям на х лет; это означает, что при обстоятельствах, благоприятных для криптоаналитика (т.е. при использовании самых современных компьютеров), защита системы может быть взломана за х лет, но никак не ранее.

14.1.3. Классические угрозы

Самая незначительная криптоаналитическая угроза — это атака только шифрованного текста (ciphertext-only attack). При использовании этого метода криптоанализа крип-тоаналитик может иметь некоторую информацию об общей системе и языке, используемом в сообщении, но единственными важными данными, имеющимися у него, является шифрованное сообщение, перехваченное из общедоступного канала.

Более серьезной угрозой для системы является атака известного открытого текста (known plaintext attack). Она включает в себя знание открытого текста и его шифрованного эквивалента. Жесткая структура большинства бизнес-форм и языков программирования часто дает оппоненту множество априорных знаний об элементах открытого сообщения. Вооруженный этим знанием и шифрованным сообщением, криптоаналитик может проводить криптоанализ с помощью известного открытого текста. Рассмотрим пример из области дипломатии: если шифрованное сообщение обязывает министра иностранных дел сделать определенное публичное заявление и он делает это, не перефразируя сообщение, криптоаналитик может получить как шифрованный текст, так и его точный перевод в открытую версию. Несмотря на то что атака известного открытого текста не всегда возможна, она используется достаточно часто, чтобы система не считалась защищенной, если она не проектировалась для противостояния такому типу атак [2].

Если криптоаналитик должен выбирать открытый текст для данного шифрованного сообщения, угроза называется атакой выбранного открытого текста (chosen plaintext attack). Во время Второй мировой войны такая атака использовалась Соединенными Штатами Америки для получения большей информации о японской криптосистеме. 20 мая 1942 года главнокомандующий Императорским Морским флотом адмирал Ямамото (Yamamoto) издал указ, детально излагающий тактику, которая должна была быть использована при атаке на острове Мидуэй. Этот указ был перехвачен подслушивающими постами союзников. К тому времени американцы узнали достаточно о японских кодах, чтобы дешифровать большинство сообщений. Однако все еще под сомнением были некоторые важные моменты, такие как место атаки. Они подозревали, что символы "AF" обозначали остров Мидуэй, но для того, чтобы убедиться, Джозеф Рошфор (Joseph Rochefort), глава военной разведки, решил использовать метод атаки выбранного открытого текста, чтобы обманным путем вынудить японцев дать конкретное доказательство. По его приказу гарнизон острова Мидэуй выдал в эфир характерное открытое сообщение, в котором остров Мидуэй сообщал, что его завод по очистке воды вышел из строя. Американским криптоаналитикам пришлось подождать всего два дня, после чего они перехватили японское шифрованное сообщение, в котором говорилось, что на AF не хватает чистой воды [1].

14.1.4. Классические шифры

Одним из ранних примеров моноалфавитного шифра был шифр Цезаря, который использовался Юлием Цезарем во времена его Галльских походов. Каждая буква исходного текста заменяется новой, полученной путем сдвига алфавита. На рис. 14.2, а изображено такое шифрующее преобразование, состоящее из трех циклических сдвигов алфавита. Если использовать этот алфавит Цезаря, сообщение "now is the time" ("время пришло!") шифруется следующим образом.

открытый текст

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

шифрованный текст

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

A

B

C

а)

	1	2	3	4	5
1	A	B	C	D	E
2	F	G	H	IJ	K
3	L	M	N	O	P
4	Q	R	S	T	U
5	V	W	X	Y	Z

б)

Рис.14.2. примеры шифров: а) алфавит Цезаря со сдвигом 3; б) квадрат Полибиуса.

Исходный текст: N O W I S T H E T I M E

Шифрованный Q R Z L V W K H W L P H

текст:

Дешифрующий ключ — это просто число сдвигов алфавита; с выбором нового ключа код изменяется. Еще одна классическая система шифрования, изображенная на рис. 14.2, б, называется квадратом Полибиуса (Polybius square). Вначале объединяются буквы I и J и трактуются как один символ (в дешифрованном сообщении значение этой "двойной буквы" легко определяется из контекста). Получившиеся 25 символов алфавита размещаются в таблицу размером 55. Шифрование любой буквы производится с помощью выбора соответствующей пары чисел — строки и столбца (или столбца и строки). Ниже приведен пример шифрования того же сообщения "now is the time" с помощью квадрата Полибиуса.

Исходный текст: N O W I S Т Н Е Т I M E

Шифрованный 33 43 25 42 34 44 32 51 44 42 23 51 текст:

Код изменяется путем перестановки букв в таблице 55.

Прогрессивный ключ Тритемиуса, который изображен на рис. 14.3, является примером полиалфавитного шифра. Строка, обозначенная как сдвиг 0, совпадает с обычным порядком букв в алфавите. Буквы в следующей строке сдвинуты на один символ влево с циклическим сдвигом оставшихся позиций. Каждая последующая строка получается с помощью такого же сдвига алфавита на один символ влево относительно предыдущей строки. Это продолжается до тех пор, пока в результате циклических сдвигов алфавит не будет смещен на все возможные позиции. Один из методов использования такого алфавита заключается в выборе первого символа шифрованного сообщения из строки, полученной при сдвиге на 1 символ, второго символа — из строки, полученной при сдвиге на 2 символа, и т.д. Ниже приведен пример сообщения, зашифрованного подобным образом.

открытый текст

a

b

c

d

e

f

g

h

i

j

k

l

m

n

o

p

q

r

t

u

v

w

x

y

z

сдвиг

0

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

1

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

A

2

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

A

B

3

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

A

B

C

4

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

A

B

C

D

5

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

A

B

C

D

E

6

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

A

B

C

D

E

F

7

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

A

B

C

D

E

F

G

8

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

A

B

C

D

E

F

G

H

9

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

A

B

C

D

E

F

G

H

I

10

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

A

B

C

D

E

F

G

H

I

J

11

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

A

B

C

D

E

F

G

H

I

J

K

12

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

A

B

C

D

E

F

G

H

I

J

K

L

13

N

O

P

Q

R

S

T

U

V

W

X

Y

Z

A

B

C

D

E

F

G

H

I

J

K

L

M

14

O

P

Q

R

S

T

U

V

W

X

Y

Z

A

B

C

D

E

F

G

H

I

J

K

L

M

N

15

P

Q

R

S

T

U

V

W

X

Y

Z

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

16

Q

R

S

T

U

V

W

X

Y

Z

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

17

R

S

T

U

V

W

X

Y

Z

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

18

S

T

U

V

W

X

Y

Z

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

19

T

U

V

W

X

Y

Z

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

20

U

V

W

X

Y

Z

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

21

V

W

X

Y

Z

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

22

W

X

Y

Z

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

23

X

Y

Z

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

24

Y

Z

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

25

Z

A

B

C

D

E

F

G

H

I

J

K

L

M

N

O

P

Q

R

S

T

U

V

W

X

Y

Рис. 14.3. Прогрессивный ключ Тритемиуса

Исходный текст: N O W I S Т Н Е Т I M E Шифрованный текст: O Q Z M X Z O M C S X Q

Существует несколько интересных способов использования прогрессивного шифра Тритемиуса. В одном из них, называемом методом ключа Вигнера (Vigener key method), применяется ключевое слово (keyword). Этот ключ диктует выбор строк для шифрования и дешифрования каждого последующего символа в сообщении. Предположим, что в качестве ключа выбрано слово "TYPE"; тогда сообщение, зашифрованное с применением метода Вигнера, выглядит следующим образом.

Ключ: T Y P E T Y P E T Y P E

Исходный текст: N O W I S T H E T I M E

Шифрованный G M L M L R W I M G B I текст:

Здесь первая буква ключа (Т) указывает, что в качестве строки для шифрования первой буквы открытого текста выбирается строка, начинающаяся с Т (сдвиг 19). Следующей выбирается строка, начинающаяся с Y (сдвиг 24), и т. д. Разновидностью этого метода является так называемый метод автоматического (явного) ключа Вигнера (Vigener auto (plain) key method), когда в качестве образующего ключа используется единственная буква или слово. Этот ключ дает начальную строку или строки для шифрования первого или нескольких первых символов открытого текста аналогично предыдущему примеру. Затем в качестве ключа для выбора шифрующей строки используются символы исходного текста. В приведенном ниже примере в качестве образующего ключа использована буква "F".

Ключ: F N O W I S T H E T I М

Исходный текст: N O W I S T H E T I M E

Шифрованный S B K E A L A L X B U Q

текст:

Метод автоматического ключа показывает, что в процесс шифрования может быть введена обратная связь. При использовании обратной связи выбор шифрованного текста определяется содержанием сообщения.

Последняя разновидность метода Вигнера — это метод автоматического (шифрованного) ключа Вигнера (Vigenere auto (cipher) key method), подобный простому методу ключа; в нем также используются образующий ключ и обратная связь. Отличие состоит в том, что после шифрования с помощью образующего ключа, каждый последующий символ ключа в последовательности берется не из символа исходного текста, а из символа шифрованного текста. Ниже приведен пример, который должен помочь понять принцип работы данного метода; как и ранее, в качестве начального ключа используется буква "F".

Ключ: F S G C K C V C G Z H T

Исходный текст: N O W I S T H E T I M E

Шифрованный S G C K C V C G Z H T X текст:

Хотя каждый символ ключа может быть найден из предшествующего ему символа шифрованного текста, функционально он зависит от всех предшествующих символов в сообщении и плюс основного ключа. Таким образом, имеется эффект рассеивания статистических свойств исходного текста вдоль шифрованного текста, что делает статистический анализ очень сложным для криптоаналитика. Слабым звеном описанного здесь примера шифрования с использованием ключа является то, что шифрованный текст содержит знаки ключа, которые будут публично выставлены через общедоступный канал "на всеобщее обозрение". Для того чтобы предотвратить такое публичное разоблачение, можно использовать вариации этого метода [3]. По нынешним стандартам схема шифрования Вигнера не является очень защищенной; основным вкладом Вигнера было открытие того, что неповторяющиеся ключевые последовательности можно создавать с использованием самих сообщений или функций от сообщений.