В синтезе электрических цепей часто прибегают к нормированию элементов и частоты. Целесообразность применения нормирования ясна из следующего примера. Пусть необходимо рассчитать частотную характеристику сопротивления последовательного RLC-контура с параметрами элементов L = 10^–5 Гн, С = 10^–9 Ф, R = = 5 Ом. Данный контур имеет добротность Q = 20, характеристическое сопротивление = 100 Ом и резонансную частоту _р = 10⁷ с^–1. При расчете сопротивления данного контура приходится оперировать с величинами от 10^–9 до 10⁷, что не всегда удобно. Выполним нормирование сопротивлений и частоты. Для этого запишем выражение сопротивления данного контура:

Разделим левую и правую часть равенства на некоторое нормирующее значение сопротивления R_н, а второе и третье слагаемое умножим и разделим на некоторое нормирующее значение частоты _н: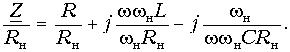

Введем следующие названия и обозначения: – нормированное комплексное сопротивление, – нормированная частота; (16.8) – нормированная индуктивность; (16.9) – нормированная емкость; (16.10) – нормированное резистивное сопротивление.

Величины _н и R_н, вообще говоря, можно выбирать произвольно. В данном случае удобно положить _н = _р и R_н = . Тогда параметры нормированных элементов принимают следующие значения:

Выполнение расчетов с такими числовыми значениями удобней, чем с ненормированными величинами.

Существует вторая, более важная причина, по которой применяют нормирование. Она проявляется в синтезе цепей. Допустим, что в результате сложных процедур получена некоторая цепь с нормированными значениями элементов. Истинные значения элементов определяются из формул (16.8)—(16.10) следующим образом: (16.11) (16.12) (16.13)

Изменяя _н и R_н можно без выполнения сложных процедур получить схемы устройств, работающих в различных диапазонах частот и при различных нагрузках. Введение нормирования позволило создать каталоги фильтров, что во многих случаях сводит сложную проблему синтеза фильтра к элементарным действиям.