Обычная аналоговая (RL-цепь) цепь описывается дифференциальными уравнениями. Если непрерывную переменную t заменить на дискретно изменяющуюся переменную nT, то дифференциальные уравнения вырождаются в разностные уравнения. Разностные уравнения общего вида, в котором в явной форме выражены прямые и обратные связи и который связывает сигналы на входе и выходе имеют следующий вид:

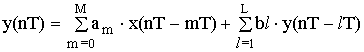– разностное уравнение общего вида,

где: x(nT) – сигнал на входе цепи,

y(nT) – сигнал на выходе,

M – число прямых отводов,

(L-1) – число обратных отводов,

m, l – целые числа,

a_m, b_m – вещественные коэффициенты.

Такому уравнению соответствуют цепи, которые называют дискретной цепью.

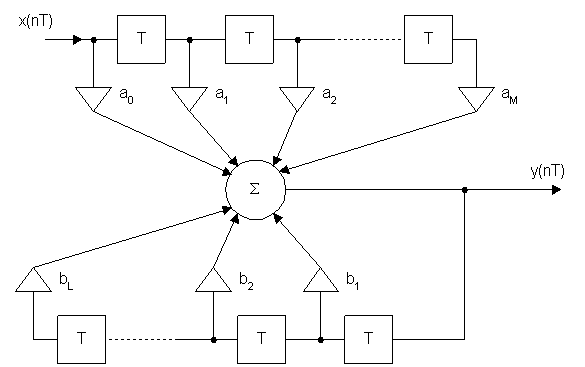
Элемент запаздывания на время T или элемент памяти.

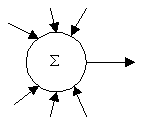Сумматор.

Т – интервал дискретизации поступающего сигнала,

a_i,b_i– умножители на коэффициент a_i или b_i.

Схема разностной цепи и значение коэффициентов a_i и b_i определяют способ обработки сигналов, поступающих на вход цепи. Расчет выходного сигнала y(nT) осуществляется путем решения разностного уравнения. Существуют аналитические и численные способы решения разностных уравнений.

Аналитические способы позволяют получить решение в общем виде, сделать анализ. Численные способы дают ответ в виде числовой последовательности.