Волновое сопротивление. Одним из вторичных параметров однородной линии является волновое сопротивление линии, определяемое через первичные параметры формулой (13.7)

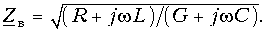
При w= 0

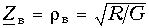
и jв = 0, т. е. волновое сопротивление чисто активное. Точно такой же характер имеет Zв при w=бесконечность;

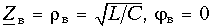
Для всех реально существующих цепей R/G > L/C, поэтому модуль волнового сопротивления с увеличением частоты уменьшается, стремясь к величине

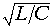
Угол jв изменяется от нулевого значения при w = 0 до нулевого значения при w=бесконечность;. Следовательно, на какой-то частоте он будет иметь максимум. Можно показать, что угол jв на всех частотах является отрицательным. На рис. 13.4 показаны графики частотных зависимостей модуля и угла волнового сопротивления однородной линии.

Чтобы выяснить физический смысл волнового сопротивления, воспользуемся выражениями для комплексных амплитуд падающих волн напряжения и тока из (13.10):

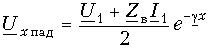
и

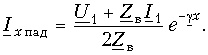
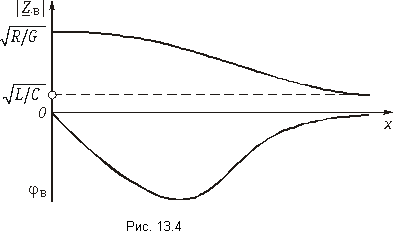
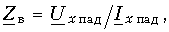
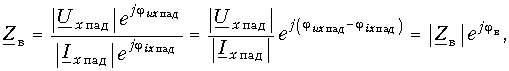
откуда

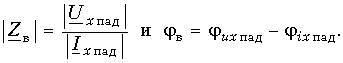
Аналогичным образом можно сказать, что

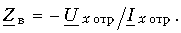
Волновое сопротивление не зависит от длины линии – оно постоянно в любой точке линии.

Пример. Определим волновое сопротивление воздушной медной линии из проводов диаметром 2r = 4 мм и расстоянием между проводами lпр = 20 см и кабельной линии с бумажной изоляцией жил диаметром 2r = 0,5 мм на частотах f = 0; 0,8 и 10 кГц для воздушной цепи и f = 0 и 0,8 кГц для кабельной цепи.

Для воздушной линии первичные параметры, взятые из справочника: R = = 2,84 Ом/км; С = 6,3 нФ/км; L = l,93 мГн/км; G = 0,57×10 См/км.

При f = 0 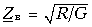=2,38 кОм. При f = 800 Гц (w= 2p 800рад/с)

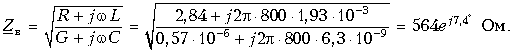
На частоте f = 10кГц wL R и wC G, поэтому

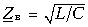= 548 Ом.

Для кабельной линии: R = 190 Ом/км, С = 50 нФ/км, L = 0,7 мГн/км, G = 5×10–4 мкСм/км. На частоте f = 0 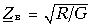= 615 кОм. Для частоты f = 800 Гц справедливо соотношение R wL и wC G. Следовательно,

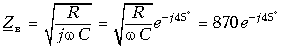Ом.

Согласованное включение линии. Рассмотрим режим работы линии, когда Zн = Zв. В этом случае коэффициенты отражения su = si = 0 и отраженные волны напряжения и тока будут отсутствовать (Uxотр = 0 и Ixотр = 0).

Напряжение и ток в любой точке линии, в том числе и на входе (x = 0), будут определяться только падающими волнами. Согласно (13.14)

,

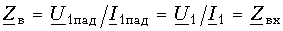т. е. входное сопротивление такой линии равно ее волновому сопротивлению. Таким образом, волновое сопротивление линии является аналогом характеристического сопротивления симметричного четырехполюсника

Указанный режим работы линии является режимом согласованного включения. При этом вся энергия поглощается в конце линии нагрузочным сопротивлением. Этот режим работы наиболее выгоден для передачи сигналов связи, так как отражение энергии от нагрузки приводит помимо увеличения рабочего ослабления линии к появлению так называемых эхо-сигналов, накладывающихся на основной сигнал и искажающих его.

Уравнения передачи однородной линии в режиме согласованного включения могут быть легко получены из (13.9 б и в), если учесть, что при согласованном включении

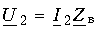
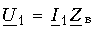
а также что

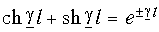
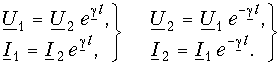
Для любой точки линии

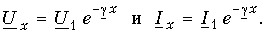(13.15 б)

Коэффициент распространения. Ко вторичным параметрам линии относится также коэффициент распространения, введенный в рассмотрение формулой (13.4):

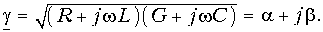
В режиме согласованного включения линии из (13.15) имеем:

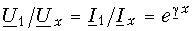
или

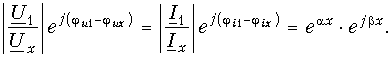
Отсюда

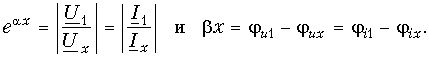
Для отрезка линии единичной длины (1 км, 1 м и т. д.) можно записать:

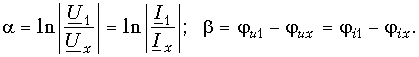
Вещественная часть коэффициента распространения a характеризует изменение напряжения и тока по абсолютной величине при распространении энергии на расстояние, равное единице длины линии. Она называется коэффициентом ослабления линии и измеряется в неперах, отнесенных к единице длины линии (в проводной связи – Нп/км, в радиосвязи – Нп/м). При использовании десятичного логарифма вместо натурального

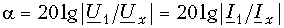
измеряется в дБ/км или дБ/м.

Мнимая часть коэффициента распространения b характеризуется изменением напряжения и тока по фазе. Она называется коэффициентом фазы линии и измеряется в рад/км или рад/м. Вместо радиан могут использоваться градусы.

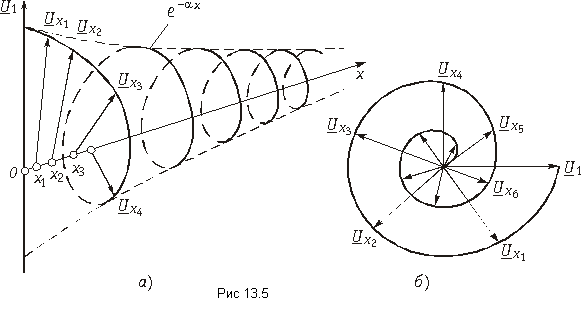
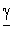
Процесс изменения напряжения (тока) вдоль согласованно нагруженной линии можно проиллюстрировать векторной диаграммой, показанной на рис. 13.5, а или так называемой спиральной диаграммой, приведенной на рис. 13.5, б

Численные значения коэффициентов a и b можно найти по первичным параметрам из общей формулы (13.4). Однако в ряде случаев можно получить более простые выражения. Так, на высоких частотах (для электрической цепи из меди, например, это частоты 10 кГц), где выполняются условия wL > R и wC > G пользуются упрощенными формулами:

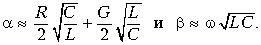
Вывод этих формул дан в специальной литературе и здесь не приводится. Для кабельных цепей в области низких частот (например, от 0 до 800 Гц) выполняются соотношения R wL и wC G. В этом случае можно показать, что a = b =

.

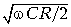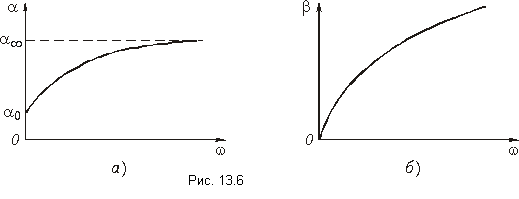
Вторичные параметры a и b зависят от частоты сложным образом. На рис. 13.6, а и б даны графики, качественно отражающие эту зависимость.

Пример. Определим коэффициент распространения воздушной медной линии c параметрами 2r = 4 мм и lпр = 20 см на частоте f = 800 Гц.

Значение коэффициента 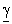найдем по полной формуле (13.4), взяв первичные параметры из предыдущего примера:

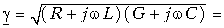
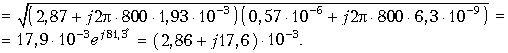
Отсюда коэффициент ослабления a = 2,86×10–3 Нп/км = 2,86 мНп/км. Перевод непер в децибелы дает a (дБ) = a (Нп)´8,7 = 24,9×10–3 дБ/км. Коэффициент фазы b = 17,6×10–3 рад/км.

Постоянная передачи длинной линии. При распространении энергии по линии на расстояние l напряжение и ток уменьшаются в e^(al) раз, а фазы напряжения и тока изменятся на величину bl

Величина al описывает ослабление напряжения и тока при распространении энергии по всей длине линии и называется характеристической (собственной) постоянной ослабления линии: Ас = al

Из формул (13.15 а) следует, что

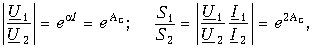
где S1 и S2 – полные мощности на входе и выходе линии. Поэтому

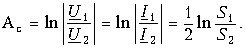
Величина Bс = al = ju1 – ju2 = ji1 – ji2 называется характеристической (собственной) постоянной фазы линии

По аналогии с теорией четырехполюсников величина Гс = Ас + jВс является характеристической (собственной) постоянной передачи линии

Заметим, что при отсутствии согласования, т. е. при Zн ¹ Zв условия передачи энергии по линии следует оценивать величиной рабочей постоянной передачи Гp = Аp + jВp по формулам, полученным в общей теории четырехполюсников.