Линии задержки. Одним из элементов гармонических корректоров являются так называемые линии задержки (ЛЗ). Идеальная линия задержки осуществляет задержку колебания на постоянную величину Dt, не изменяя энергии этого колебания. Очевидно, модуль передаточной функции (АЧХ) ЛЗ равен 1, а угол (ФЧХ) j(w) = -wЧDt. Таким образом, передаточная функция линии задержки

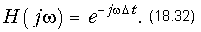
Однако данная функция не удовлетворяет УФР, так как j(w) не является тангенс-функцией. В реальной линии задержки ГВП является постоянным только с определенной степенью точности в заданном диапазоне частот. Будем рассматривать низкочастотные ЛЗ, рабочий частотный диапазон которых простирается от нуля до частоты w. Совершенно очевидно, что ЛЗ являются частным случаем фазового корректора (ФК). Отличие состоит в том, что от ФК требуется воспроизвести частотную характеристику ГВП, вообще говоря, произвольной формы, в то время как ЛЗ обладает только постоянным, с заданной степенью точности, групповым временем. В связи с этим есть возможность заранее рассчитать набор ЛЗ для различных значений ГВП и различной точности его воспроизведения и оформить результаты в виде каталогов. Как и в случае аппроксимации характеристик фильтров, применяется как равноволновая аппроксимация, так и аппроксимация монотонными характеристиками. Определим далее общий вид операторной передаточной функции ЛЗ. Во-первых, знаменатель любой передаточной функции должен быть полином Гурвица v(p). Во-вторых, непосредственной подстановкой легко убедиться, что модуль комплексной передаточной функции равен единице, если в числителе находится полином, сопряженный полиному знаменателя. Поэтому в самом общем виде комплексная передаточная функция ФК или ЛЗ имеет вид

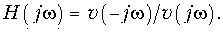
Заменив jw на р, получим операторную передаточную функцию

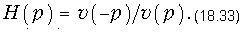
Как видим, вся информация о передаточной функции содержится в полиноме Гурвица. Так, фазовая характеристика четырехполюсника равна удвоенному аргументу полинома при р = jw

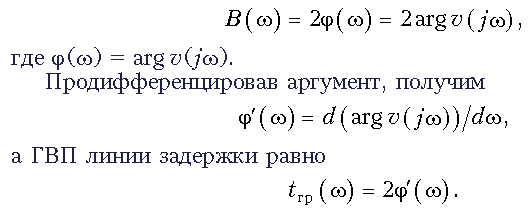
Мы уже убедились, что при построении каталогов удобно применять нормированные величины. В данном случае это нормированная частота W = w/wн и нормированное ГВП . При синтезе ЛЗ частота нормирования wн находится из условия, что на нулевой частоте нормированная функция , а ГВП равно 2, т. е.

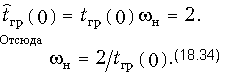
Аппроксимация ГВП гладкими функциями осуществляется на основе полиномов Бесселя, которые имеют следующий вид:

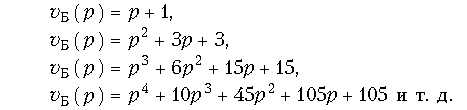
Графики нормированной функции показаны на рис. 18.41. Задача аппроксимации максимально-гладкими функциями решена аналитически с помощью рядов Тейлора. Задаваясь погрешностью аппроксимации D, легко получить нормированные граничные частоты рабочей полосы линии задержки. На рис. 18.41 проведена линия на уровне 0,9, что отвечает 10% погрешности. Существуют справочники, в которых приведены таблицы, содержащие граничные нормированные частоты при различных порядках полинома Бесселя п и различных погрешностях. Зная полином Бесселя нетрудно численно найти координаты его корней, которые являются полюсами передаточной функции. Напомним, что в соответствии с (18.33) каждому полюсу в левой полуплоскости соответствует нуль в правой, т. е. p0k = -pk. Координаты корней полиномов Бесселя приведены в справочниках. Рассмотрим порядок синтеза ЛЗ с максимально-плоской характеристикой группового времени. При синтезе заданными величинами являются групповое время tз, рабочий диапазон частот 0 ... w1, погрешность аппроксимации D. Согласно (18.34) находим частоту нормирования wн при условии, что tгр(0) = tэ. Зная wн рассчитываем нормированную граничную частоту w1/wн = W1. Пользуясь графиками или таблицами, находим минимальный порядок передаточной функции ЛЗ, при которой граничная частота рабочей полосы частот равна или превышает W1. Найденному порядку соответствует полином Бесселя vБ(p). Таким образом, получена передаточная функция в виде

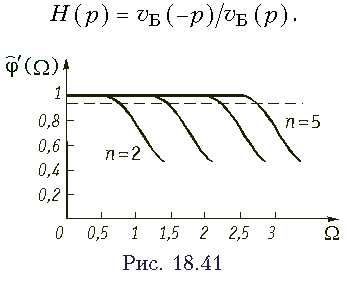
Зная координаты корней полинома Бесселя, передаточную функцию можно представить в виде произведений функций второго порядка и каждую функцию реализовать фазовым звеном, как это было рассмотрено ранее. Напомним, что при нечетном порядке т одна из функций будет первого порядка. Решить задачу равноволновой аппроксимации аналитически трудно, поэтому она решается численными методами и в справочниках приведены такие же таблицы, как и в случае аппроксимации максимально гладкими функциями. Поэтому порядок синтеза ЛЗ с равноволновыми характеристиками группового времени остается прежним, как и в случае монотонных характеристик.

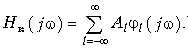
Гармонические корректоры. Как уже отмечалось, параметры тракта передачи нуждаются в окончательной коррекции. Для этой цели применяются регулируемые корректоры, которые, как правило, настраиваются автоматически. Теория таких корректоров заключается в том, что передаточную функцию корректора, которая является с точностью до постоянной обратно пропорциональной по отношению к линии передачи, раскладывают в ряд по системе ортогональных функций: Если в качестве базисной функции jl(jw) выбрать передаточную функцию ЛЗ, то получится ряд Фурье в комплексной форме:

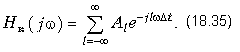
коэффициенты которого

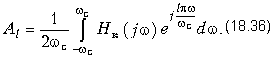
Сделаем важные замечания: 1. Ряд Фурье применяется для разложения периодических функций. Поэтому АЧХ и ФЧХ такого корректора также будут периодическими. Интервал [-wс, wс] является рабочим. 2. Так как АЧХ линии передачи является четной функцией, а ФЧХ - нечетной, то коэффициенты (18.36) в разложении ряда Фурье (18.35) являются вещественными числами. 3. Для ускорения сходимости ряда из фазочастотной характеристики линии вычитают линейную составляющую, что устраняет разрывы ФЧХ на границах интервала. Попытаемся реализовать передаточную функцию (18.35). Из данного ряда следует, что передаточная функция корректора получается путем умножения передаточных функций линий задержки на вещественные числа с последующим суммированием. Однако, точная реализация функции (18.35) невозможна, так как требует бесконечного числа ЛЗ, поэтому ее реализуют приближенно, ограничиваясь конечными числами слагаемых с отрицательными (m) и положительными (n) индексами

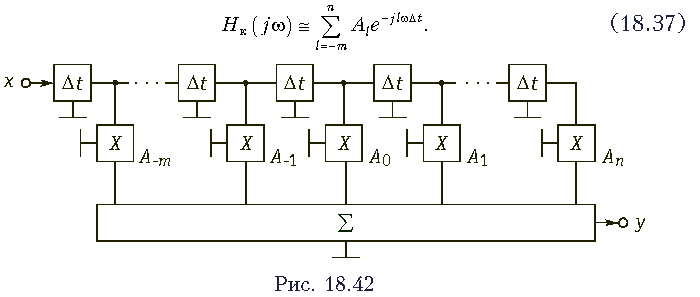
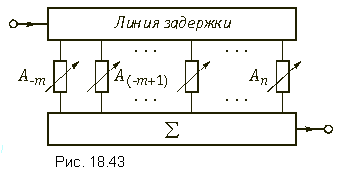
Даже после усечения ряда, передаточная функция остается нереализуемой. Во-первых, передаточная функция ЛЗ не удовлетворяет УФР. Во-вторых, при отрицательных значениях l ФЧХ линии задержки равна |l|Dtw, а ее групповое время t = -dj(w)/dw - |l|Dt является отрицательным. В данном случае это означает, что нарушается причинно-следственная связь и колебание на выходе появляется раньше, чем на входе. Данная трудность легко преодолевается, если допустить что корректор вносит постоянную задержку tгр = (m+1)Dt. С учетом сказанного, функциональную схему корректора представляют в виде, показанном на рис. 18.42. Колебание х, поступающее на вход корректора, задерживается первой ЛЗ на время Dt и поступает на входы умножителя и следующей ЛЗ. Колебание, поступившее на вход второй ЛЗ, задерживается дополнительно на время Dt так, что общая задержка составляет 2Dt. Задержанное на эту величину колебание поступает на вход третьей ЛЗ и вход второго умножителя и т. д. Задержанные на величины Dt, 2Dt, 3Dt ... колебания суммируются, образуя колебание y. Таким образом, получается с точностью до множителя e(m+n)Dt передаточная функция (18.37). Умножитель в простейшем случае представляет собой делитель напряжения. Регулировка (настройка) корректора осуществляется с помощью изменения коэффициентов Аl. На практике изменяется коэффициент деления делителя. Для упрощения изображения схемы гармонического корректора каскадное соединение линии задержки заменяют одной ЛЗ с отводами, а умножители -переменным сопротивлением (кроме этого не показывают заземленных проводов). Соответствующая данным упрощениям схема гармонического корректора показана на рис. 18.43. Частным случаем гармонического корректора является косинусный корректор. Он получается когда число отводов слева и справа от нулевого одинаково и соответствующие коэффициенты с положительными и отрицательными индексами равны между собой, т. е. А-l = Аl. Тогда попарные суммы дают косинусоидальную функцию

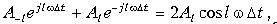
а выражение (18.37) примет вид

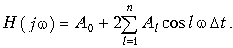
Полученная функция является вещественной, а значит может применяться только для коррекции АЧХ.

В данном параграфе изложены только основы построения гармонических корректоров в диапазоне частот 0 ... w1. Здесь не рассмотрены полосовые корректоры, алгоритмы автоматической настройки корректоров, а также корректоры с обратными связями и ряд других вопросов, которые изучаются в специальных курсах.