2.1. Понятие случайной величины

2.2. Дискретные случайные величины

2.1. Понятие случайной величины

Случайной величиной называется величина, которая в результате испытаний принимает то или иное значение.

1. Опыт бросания монеты 2 раза {ГГ, ГР, РГ, РР}
2. Бросание кубика
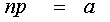
3. Схема Бернулли – 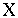число успехов в 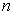испытаниях
4. Стрельба по мишени, 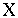– расстояние от точки попадания до центра
5. Группа из 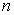человек, 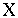– число мальчиков
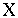6. – время до отказа одного прибора
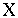7. – вес случайного студента

Дискретные случайные величины – это величины, которые могут принимать конкретное или счетное число значений.

Непрерывные случайные величины – это величины, которые могут принимать несчетное множество значений.

2.2. Дискретные случайные величины

Закон распределения есть соответствие между значениями случайных величин и их вероятностями.

Может задаваться:

1. Таблично

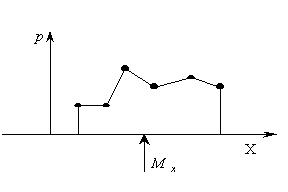
2. Графически

3. Аналитически

1. Таблично

• ряд распределения

В общем виде:

Свойства ряда распределения:

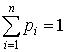– условие нормировки

Пример:

В 2-х бросаниях монеты: – число "гербов"

2. Графически

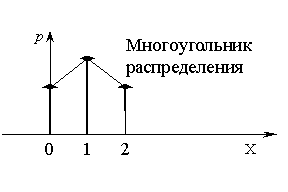
3. Аналитически

Пусть – испытаний

– число успехов

Функция распределения

Свойства функции распределения:

• 
• 
• 
• 
• 
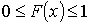
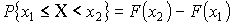
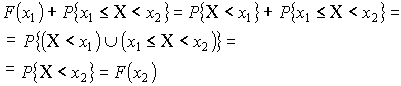
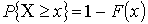
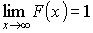
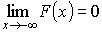
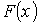• – не убывающая функция
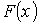• – непрерывна слева

Пусть задан ряд распределения

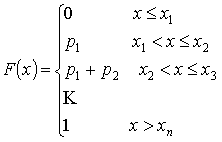
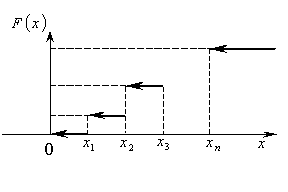
Числовые характеристики дискретных случайных величин.

1. 1. Математическое ожидание 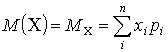– среднее значение

Пример:

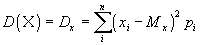
1. 1. Дисперсия

Дисперсия характеризует разброс значений случайной величины от её математического ожидания.

Пример:

1. Среднеквадратическое отклонение (СКО)