Пусть – спектр дискретного сигнала x(nТ);

(jω) – спектр исходного аналогового сигнала x(t).

Для установления связи между спектрами воспользуемся прямым преобразованием Фурье:

Раскладываем в ряд Фурье:

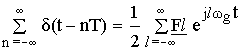
Fl– амплитуда гармоник.

Определим Fl используя формулу связи между спектрами периодических и непериодических сигналов.

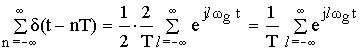
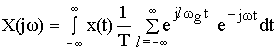
В силу линейности операции в этом выражении знаки и можно поменять местами.

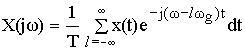
Воспользуемся теоремой смещения (теорема о спектрах).

Если 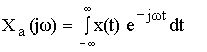, то:

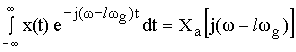
Формула связи спектров дискретного и аналогового сигналов имеет вид:

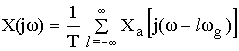
Вывод: спектр дискретного сигнала равен сумме равно-смещенных спектров аналогового сигнала, сдвинутых на величину кратных .

Полученный результат продемонстрируем на графиках.

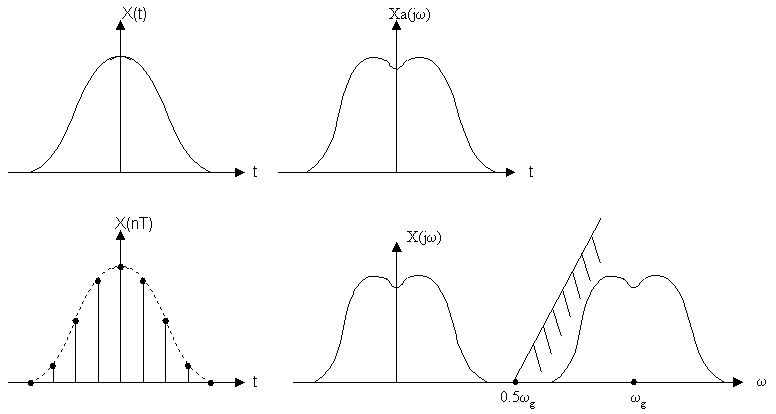
Если , то спектр дискретного и аналогового сигналов совпадает (X(jω) и X_a(jω) совпадают) на интервале [-0.5ω_g;0.5ω_g]. В результате x(t) аналоговый сигнал можно восстановить применением ФНЧ с частотой среза ω_с=0.5ω_g.

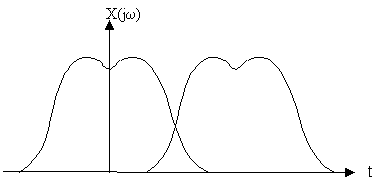
Если ω_в>0.5ω_g, то смежные спектры перекрываются и возникают ошибки наложения, погрешности (не устранимые), поэтому восстановить такой сигнал можно только с искажением (искажения могут оказаться значительными).