Одним из условий применимости преобразования Фурье функции , описывающей форму сигнала, является ее абсолютная интегрируемость, что означает конечную энергию сигнала. Вместе с тем в ряде случаев спектрально удовлетворяющих этому условию. Это может быть гармоническое колебание, используемое в качестве несущего колебания при осуществлении операции модуляции, сигналы, описываемые единичной функцией и др. Однако, и на эти сигналы может быть распространен аппарат преобразования Фурье.

Рассмотрим сначала сигнал вида

.

Очевидно такой сигнал обладает бесконечной энергией. Применим формально к этому сигналу преобразование Фурье (2.27)

.

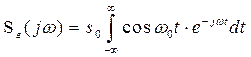Так как

,

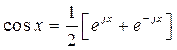то (2.54) можно переписать следующим образом

.

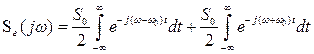Воспользовавшись табличным интегралом

,

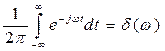где – рассмотренная выше - функция.

Тогда, с учетом этого выражения, получим

.

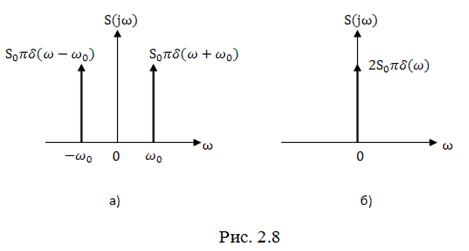
Из (2.55) следует, что спектр гармонического колебания определенного на интервале времени , равен нулю на всех частотах, кроме и . На этих частотах значение спектральных составляющих обращается в бесконечность (рис. 2.8, а)

Если положить , что соответствует постоянному сигналу , то из (2.55) следует

.

Таким образом, спектр постоянного сигнала отличен от нуля только при (рис. 2.8,б). На этой частоте значение спектральной составляющей равно бесконечности.

Можно показать [Л.3], что спектр ступенчатого сигнала

,

равен

.

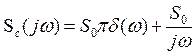Из выше изложенного следует, что спектры неинтегрируемых сигналов можно вычислить, используя преобразование Фурье с привлечением математической абстракции – - функции. Тогда возникает вопрос: а что же представляет собой спектр сигнала, форма которого описывается - функцией, т.е.

.

Применяя (2.27) к этому сигналу и учитывая фильтрующее свойство -функции, получим

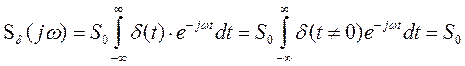. (2.56)

Следовательно сигнал, представляющий собой произведение на - функцию (на практике – очень короткий импульс очень большой амплитуды) имеет равномерный спектр по всему диапазону частот. Этот важный для радиотехнических задач вывод будет использован в дальнейшем.