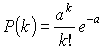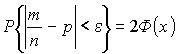1.2. Алгебра событий (Булева алгебра)
1.5. Вероятность появления хотя бы одного из события
1.1. Случайное событие
Опыт или случайное событие – действие или ряд действий, который может быть повторен многократно, и который заканчивается не некоторым исходом.
Опыт:
![]() - исход
- исход
![]() - пространство элементарных исходов. Все исходы равно возможны.
- пространство элементарных исходов. Все исходы равно возможны.
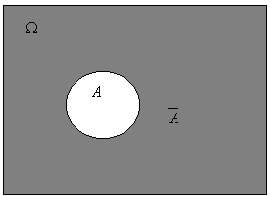
Случайным событием называется подмножество множества ![]()
![]() .
.
Случайным событием называется событие, которое в результате данного опыта может произойти, а может и не произойти.
![]() - называются совместными, если в результате опыта элементарный исход принадлежит
- называются совместными, если в результате опыта элементарный исход принадлежит ![]() и
и ![]() .
. ![]()
![]() - несовместны.
- несовместны.
![]() - невозможное событие, если оно не имеет элементарных исходов
- невозможное событие, если оно не имеет элементарных исходов ![]()
![]() - достоверное, если оно в результате опыта обязательно произойдет.
- достоверное, если оно в результате опыта обязательно произойдет.
Вероятность случайного события некоторая числовая характеристика или мера этого события.
![]()
![]()
![]()
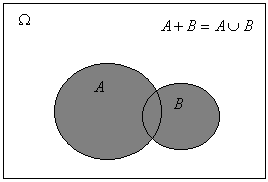
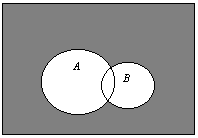
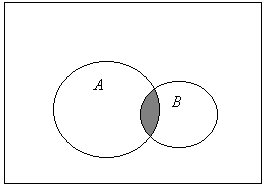
![]() - сумма событий (сложение) – событие состоящие в том, что произойдет A или B или оба.
- сумма событий (сложение) – событие состоящие в том, что произойдет A или B или оба.
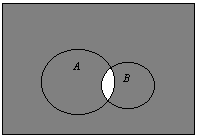
![]() - это событие, состоящее в том, что произойдет и A и B вместе.
- это событие, состоящее в том, что произойдет и A и B вместе.
![]() - отрицание события A.
- отрицание события A.
![]()
Диаграмма Эйлера-Венна.
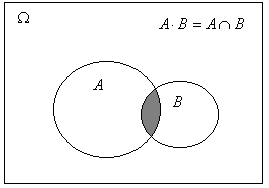
1.2. Алгебра событий (Булева алгебра)
Свойства операций:
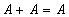
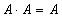
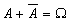
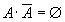
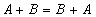
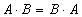
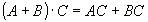
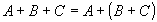
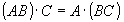
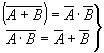 Правило Моргана
Правило Моргана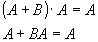
![]()
![]()

![]()
![]()

![]() - противоположное событие (отрицание).
- противоположное событие (отрицание).
Пусть ![]() - события, что
- события, что ![]() (несовместимые между собой)
(несовместимые между собой)
![]() - образуют достоверное событие
- образуют достоверное событие ![]()
![]() - полная группа событий
- полная группа событий
1.3. Вероятность
Аксиоматическое определение вероятности
Опыт.
![]() ММ,ДМ,МД,ДД
ММ,ДМ,МД,ДД ![]()
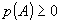 - аксиома не отрицательности.
- аксиома не отрицательности.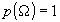 - аксиома нормированности.
- аксиома нормированности.- Аксиома одитивности.
![]() , если
, если ![]() и
и ![]() несовместны.
несовместны.
![]() - статистическая вероятность(относительная частота события
- статистическая вероятность(относительная частота события![]() )
)
![]() - число благоприятных исходов.
- число благоприятных исходов.
![]() - число всего опытов.
- число всего опытов.
Классическая вероятность
![]() - конечное множество состоит из
- конечное множество состоит из ![]() элементарных исходов.
элементарных исходов. ![]()
![]() , где
, где ![]() - это общее число всех исходов, а
- это общее число всех исходов, а ![]() - это число благоприятствующих исходов.
- это число благоприятствующих исходов.
![]()
Формулы комбинаторики
- Перестановки из
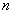 элементов - это упорядоченное множество из
элементов - это упорядоченное множество из 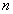 элементов, число перестановок
элементов, число перестановок 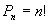 .
. - Сочетания из
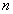 элементов по
элементов по 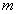 элементов - называется подмножества
элементов - называется подмножества 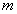 элементов из
элементов из 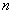 , без повторений.
, без повторений.
![]()
- Размещение из
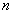 элементов по
элементов по 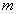 - упорядоченное подмножество
- упорядоченное подмножество 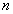 элементов из
элементов из 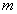 элементов.
элементов.
![]()
Схема урн
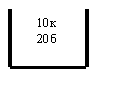
![]() = “2”к и “3”б
= “2”к и “3”б
![]()
![]() = “5”б
= “5”б
![]()
Геометрическая вероятность
![]()
1)
2)
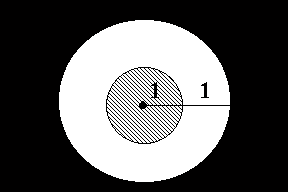
Задача о встрече:
![]()
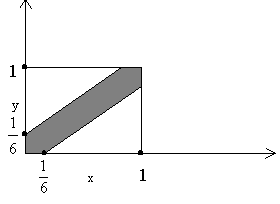
![]()
![]()
![]()
![]()
![]()
Теорема сложения
- Пусть
 и
и 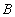 - несовместны тогда
- несовместны тогда 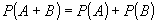 .
. - Пусть
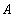 и
и 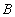 - совместны тогда
- совместны тогда  .
.
Доказательство:
![]()
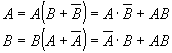
![]()
![]()
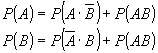
Пример:
![]() - “курит”
- “курит” ![]() .
.
![]() - “живет в общежитии”
- “живет в общежитии” ![]() .
.
![]()
![]()
![]()
1.4. Условная вероятность
![]() и
и ![]() - называются независимыми, если вероятность события
- называются независимыми, если вероятность события ![]() не зависит от того, произошло ли событие
не зависит от того, произошло ли событие ![]() и наоборот.
и наоборот.
![]() - условная вероятность события
- условная вероятность события ![]() при условии, что событие
при условии, что событие ![]() произошло.
произошло.
![]()
Теорема умножения
![]()
Если ![]() и
и ![]() - независимы, то
- независимы, то ![]() .
.
Пример:
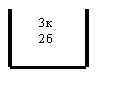
![]() - 1й - б
- 1й - б
![]() - 2й - б
- 2й - б
![]()
![]()
Теорема умножения для 3-х событий
![]()
Пример:
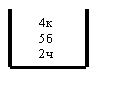
![]() - 1й - б
- 1й - б
![]() - 2й - к
- 2й - к
![]() - 3й - ч
- 3й - ч
![]()
1.5. Вероятность появления хотя бы одного из события
Опыт:
Двое стреляют
![]() - вероятность попадания 0,8.
- вероятность попадания 0,8.
![]() - вероятность попадания 0,6.
- вероятность попадания 0,6.
A - вероятность, что хотя бы один попал.
![]()
![]() - оба промаха.
- оба промаха.
![]()
![]() - произошло хотя бы одно событие из
- произошло хотя бы одно событие из ![]() .
.
![]() - ни одно из событий не произошло.
- ни одно из событий не произошло.
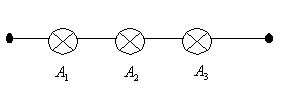
![]() - перегорит лампа.
- перегорит лампа.
![]() - цепь не работает.
- цепь не работает.
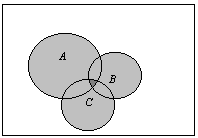
1.6. Формула полной вероятности
Пусть А – событие, которое происходит при наступлении одного из ![]() событий, которые образуют полную группу.
событий, которые образуют полную группу.
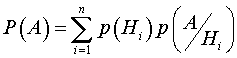
Доказательство:
![]()
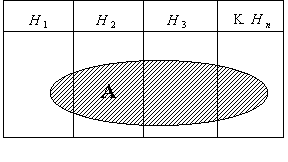
![]() – несовместны
– несовместны
Пусть ![]() , тогда
, тогда ![]()
![]() ,
, ![]() , …,
, …, ![]() – гипотезы
– гипотезы
Из всех групп выбирается только одна.
Пример:
Идет сдача экзамена
I – 20
II – 10
III – 15
![]() – студент
– студент ![]() сдал экзамен
сдал экзамен
![]() – случайно выбранный студент сдал экзамен
– случайно выбранный студент сдал экзамен
![]()
![]()
![]()
![]()
1.7. Формула Бейеса
Пусть событие ![]() уже произошло, тогда какова вероятность того, что произошло событие
уже произошло, тогда какова вероятность того, что произошло событие ![]() .
.
Полная вероятность 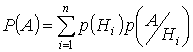 , отсюда
, отсюда
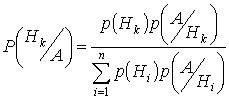
Доказательство:
![]()
Пример:
Полная вероятность ![]()
Пусть ![]() произошло, тогда
произошло, тогда 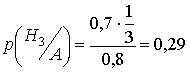
1.8. Повторение независимых испытаний. Схема Бернулли
Испытания независимы, если вероятность элементарных исходов не зависят от предыдущих испытаний.
![]() – число независимых испытаний
– число независимых испытаний
![]() – может произойти с вероятностью
– может произойти с вероятностью ![]()
С какой вероятностью событие ![]() произойдет
произойдет ![]() раз
раз
![]() , где
, где
![]() – вероятность успеха
– вероятность успеха
![]() – вероятность неуспеха
– вероятность неуспеха
![]() – число сочетаний способов
– число сочетаний способов
Доказательство:
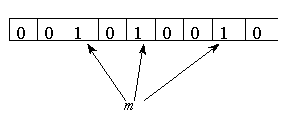
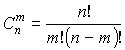
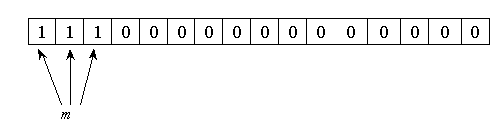
![]()
Пример:
10 раз бросим монету, какова вероятность того герб выпадет 5 раз
![]()
![]()
![]()
![]()
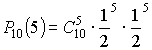
Вероятность того, что событие произойдет от ![]() до
до ![]() раз в
раз в ![]() испытаниях:
испытаниях:
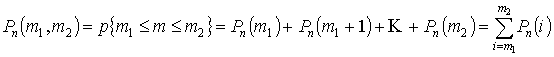
Приближенные формулы в схеме Бернулли.
Локальная теорема Муавра – Лапласа
Если ![]() достаточно велико, то вероятность в схеме Бернулли
достаточно велико, то вероятность в схеме Бернулли
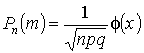 , где
, где
![]() – количество испытаний
– количество испытаний
![]() – вероятность успеха
– вероятность успеха
![]() – вероятность неуспеха
– вероятность неуспеха
![]() – функция Гаусса
– функция Гаусса
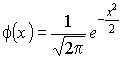 , где
, где 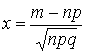 ,
, ![]() – ожидаемое количество успехов
– ожидаемое количество успехов
Пример:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Свойства функции Гаусса:
![]() – четная функция
– четная функция
![]()
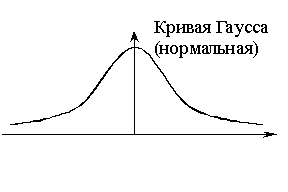
![]() – наивероятнейшее число успехов
– наивероятнейшее число успехов
Пример:
![]()
![]()
Наивероятнейшее число успехов ![]()
Интегральная теорема Муавра – Лапласа
Пусть ![]() – число испытаний (очень велико), тогда
– число испытаний (очень велико), тогда
![]() , где
, где
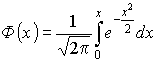 – функция Лапласа
– функция Лапласа
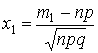
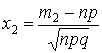
Свойства функции Лапласа:
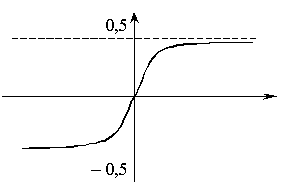
Функция нечетная, то есть ![]()
![]()
![]()
![]()
![]()
![]()
Пример:
![]()
![]()
![]()
![]()
|
|
Правило трех сигм
![]()
![]()
Пример:
![]()
![]()
![]()
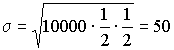
![]()
Формула Пуассона
Если ![]() достаточно велико, а
достаточно велико, а ![]() мало
мало
![]() – среднее значение успехов в
– среднее значение успехов в ![]() испытаниях.
испытаниях.
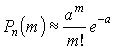 , где
, где ![]()
Пример:
![]() вызовов в час, какова вероятность того, что в течении 1 мин поступит
вызовов в час, какова вероятность того, что в течении 1 мин поступит ![]() вызовов.
вызовов.
![]()
![]()
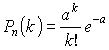
|
Отклонение частоты вероятности |
|
Пример:
![]()
![]()
![]()
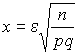
![]()
Парадокс раздачи подарков:
-
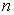 – человек. Какова вероятность того, что каждому достанется свой подарок.
– человек. Какова вероятность того, что каждому достанется свой подарок.
![]()
При ![]()
![]()
![]()
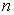 – подарков,
– подарков, 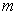 – человек. Какова вероятность того, что какой – то человек получит
– человек. Какова вероятность того, что какой – то человек получит 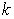 подарков.
подарков.
По формуле Пуассона:
![]() – среднее число подарков
– среднее число подарков