Линейное программирование – программа математических действий, позволяющая находить оптимальные решения экономических задач, условия и цель которых могут быть выражены в виде линейных выражений или неравенств.

В основе линейного программирования лежат две базовые модели:

• транспортная;

• общая или модель симплексная.

По типу транспортной задачи в связи решаются вопросы оптимального построения сетей, распределения потоков обмена на сети и распределения капитальных затрат по объектам строительства. Условные обозначения: А_i – пункты отправления (поставщики), i = 1, 2, 3, … m; В_j – пункты назначения (потребители), j = 1, 2, 3, … n; Q_i – возможности пунктов отправления; q_j – потребности пунктов назначения; С_ij – стоимость перевозки груза из пункта i в пункт j; х_ij – количество перевозимого груза из пункта i в пункт j.

Общая формулировка задачи: имеются m поставщиков (пунктов отправления) и n потребителей (пунктов назначения). Известна возможность каждого поставщика Q_i и спрос каждого потребителя qj. Известна стоимость перевозки единицы груза от каждого i-го поставщика каждому j-ому потребителю – С_ij.

Задача состоит в том, чтобы найти такой вариант закрепления потребителей (пунктов назначения) за поставщиками (пунктами отправления), при котором общие затраты на транспортировку грузов были бы min, то есть стоимость перевозки груза является критерием оптимальности для данной задачи.

Особенность транспортной задачи: распределению подлежит однородная или взаимозаменяемая продукция.

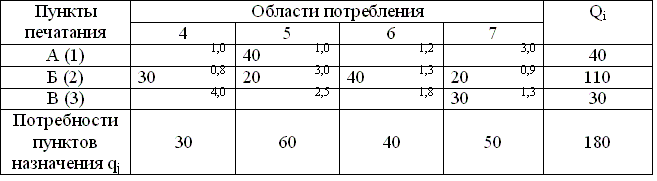
Все исходные данные представляются в виде таблицы.

Таблица 7.1. Исходные данные для транспортной задачи

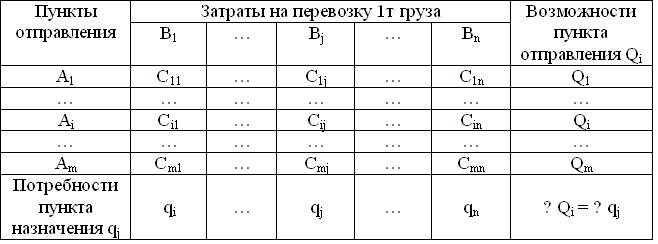
Транспортная задача, в которой суммарная возможность всех поставщиков совпадает с суммарным спросом всех потребителей, имеет закрытую транспортную модель

Q_i = q_j (7.1)

Если эти величины не сбалансированы, то у задачи открытая транспортная модель.

Прежде, чем моделировать, необходимо от открытой модели перейти к закрытой. В соответствии с условиями задачи вводится либо условный поставщик, либо условный потребитель. Возможность условного поставщика или спрос условного потребителя определяются как разность между Q_i и q_j. Но так как перевозка от условного поставщика или к условному потребителю не производится, то в соответствующей строке (столбце) используются нулевые оценки.

Модель задачи: это система уравнений и неравенств, которые включают функцию цели (критерий оптимальности) и систему ограничений по возможностям пунктов отправления и по потребностям пунктов назначения.

Целевая функция:

Z = C₁₁*x₁₁ + C₁₂*x₁₂ + … + C_1j*x_1j + C_2j*x_2j + … + C_mn*x_mn > min (7.2)

Или

C_ij*x_ij > min

Система ограничений по возможностям:

илиx_ij Q_i (7.4)

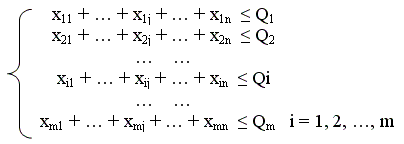
Система ограничений по потребностям:

или

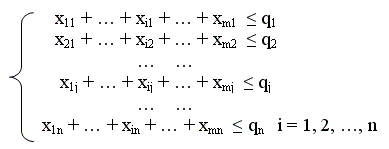
x_ij q_i (7.5)

Число уравнений и неравенств значительно меньше, чем число неизвестных, поэтому решить их подстановкой нельзя. Для этого разработан метод линейного программирования (во всех уравнениях в модели задачи Х в первой степени – линейные уравнения – отсюда название линейное программирование).

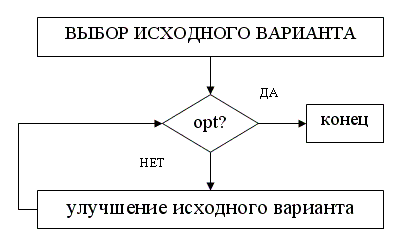
Рисунок 7.1. Алгоритм решения задач линейного программирования (проверка на оптимальность)

Исходный вариант:

1. Метод северо-западного угла
2. Метод минимального элемента

Пример расчета

Закрепить пункты децентрализованного печатания газет за соседними областями так, чтобы затраты на перевозку газет были бы минимальными.

Таблица 7.2. Решение транспортной задачи методом северо-западного угла (матрица 1)

Модель задачи:

Z = x_ijC_ij > min

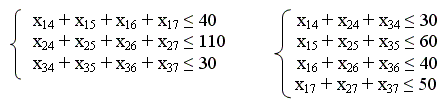
уравнения + неравенства = 8 (m + n + 1)
неизвестных = 12

Решение задачи.

I этап. Выбор исходного варианта с использованием способа северо-западного угла заключается в механическом заполнении матрицы без учета стоимости перевозки единицы груза (цифра в правом верхнем углу ячейки матрицы). Заполнение начинается с левого верхнего угла. На каждом шаге осуществляется переход в соседнюю клетку вниз и вправо. В данном примере: в область потребления 4 необходимо q_j = 30 тыс. экземпляров газет, а возможности составляют Q_i = 40 тыс. экземпляров газет, следовательно, в квадрат 1-4 заносим цифру 30, а остаток 10 пойдет в область 5. В область 5 необходимо 60 тыс. экземпляров газет, но возможности пункта печатания 1 составляют лишь 10 тыс. экземпляров, поэтому в квадрат 1-5 заносим цифру 10, а оставшиеся необходимые 50 тыс. экземпляров заносим в квадрат 2-5, т. к. возможности пункта печатания 2 позволяют это сделать (они составляют 110 тыс. экземпляров). В область потребления 6 необходимо 40 тыс. экземпляров, в квадрат 2-6 заносим цифру 40. В область 7 нужно 50 тыс. экземпляров, но остаток возможностей пункта печатания 2 составляет 20 тыс. экземпляров, поэтому в квадрат 2-7 пишем 20, а оставшиеся необходимые 30 тыс. экземпляров поставит пункт печатания 3, и в квадрат 3-7 пишем 30. Далее необходимо проверить, что модель закрытая, т. е.

Q_i = q_j

Функция цели: Z₁ = 30*10 + 10*10 + 50*30 + 40*1,3 + 20*0,9 + 30*1,3 = 299 тыс. руб.

Для проверки на оптимальность нужно, чтобы выполнялось требование: число заполненных клеток = m + n – 1.

Если это требование не выполнено, то меняются местами столбцы или строки, чтобы раздробить значения Х_ij.

II этап. Проверка на оптимальность осуществляется путем анализа свободных клеток, где х = 0. Поочередно в пустые клетки добавляются единицы, тем самым нарушая баланс. Чтобы сохранить баланс, необходимо проследить цепочку изменений по замкнутому контуру (например, квадраты 1-4, 1-5, 2-5, 2-4). Вершинам контура присваиваются знаки: в пустую клетку “+” (ее нужно сделать как бы занятой, т. е. добавить груз), а далее знаки чередуются “-”, “+”, “-” и т. д. Конфигурации контуров могут быть самые разные:

Рисунок 7.2. Конфигурации контуров

Для каждого контура рассчитывается прирост транспортных затрат (ПТЗ) как алгебраическая сумма (с учетом знаков) цен перевозки единицы груза всех вершин контура.

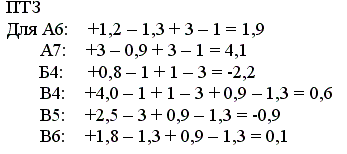
Если хотя бы одна клетка имеет отрицательный ПТЗ, это значит, что вариант неоптимальный и его можно улучшить.

III этап. Улучшение исходного варианта осуществляется по наиболее отрицательному значению пустой клетки. Здесь это клетка Б4. В данной области происходит перераспределение количества груза по контуру (рис. 7.3).

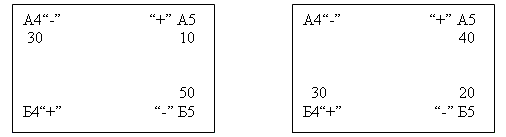
Рисунок 7.3. Перераспределение количества груза по контуру

Правило перераспределения: из отрицательных значений вершин выбирается меньшее (здесь А4 30), и из отрицательных вершин это число отнимается, а к положительным – прибавляется.

Строится новая матрица.

Таблица 7.3. Решение транспортной задачи методом северо-западного угла (матрица 2)

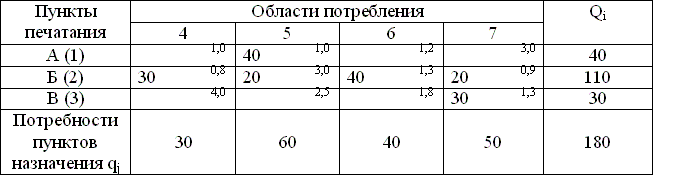
Тогда функция цели: Z₂ = 40*1,0 + 30*0,8 + 20*0,3 + 40*1,3 + 20*0,9 + 30*1,3 = 233 тыс. руб.

Полученный вариант проверяем на оптимальность, и если все ПТЗ положительны, то задача решена. В противном случае необходимо осуществить перераспределение количества груза и т. д.

Нахождение исходного варианта способом минимального элемента (стоимости перевозки груза).

Таблица 7.4. Решение транспортной задачи методом наименьшего элемента

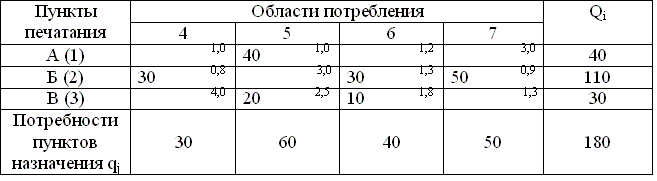
Таблица 7.5. Вспомогательная таблица для решения задачи методом наименьшего элемента

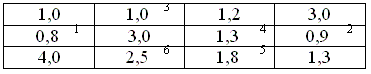
Первым заполняется квадрат с наименьшим значением стоимости перевозки груза. Затем квадраты по возрастанию стоимости в соответствии с потребностями пунктов назначения и возможностями пунктов отправления.

Выполняется проверка на оптимальность и далее аналогично решению способом северо-западного угла.

Способ минимального элемента позволяет быстрее находить оптимальный вариант решения задачи, возможно даже сразу.