1.1. Гауссовский канал, общая задача приема, оптимальные решающие правила
1.4. Обмен выигрыша от ортогонального кодирования на ширину полосы
1.5. Примеры множеств ортогональных сигналов
1.5.1. Кодирование временным сдвигом
1.1. Гауссовский канал, общая задача приема, оптимальные решающие правила
Любая информационная система, в которой данные передаются из одной пространственной точки в другую, может быть представлена следующей абстрактной моделью. Пусть имеется некоторый источник, генерирующий одно из ![]() возможных сообщений. Каждое из
возможных сообщений. Каждое из ![]() конкурирующих сообщений передается своим специфическим сигналом, так что имеется множество
конкурирующих сообщений передается своим специфическим сигналом, так что имеется множество ![]() из
из ![]() возможных сигналов:
возможных сигналов: ![]() . Источник выбирает некоторый определенный сигнал
. Источник выбирает некоторый определенный сигнал ![]() и подает его на вход канала (см. рисунок). На приемной стороне (на выходе канала) наблюдается принятое колебание
и подает его на вход канала (см. рисунок). На приемной стороне (на выходе канала) наблюдается принятое колебание ![]() , которое является не точной копией переданного сигнала
, которое является не точной копией переданного сигнала ![]() , а результатом трансформации
, а результатом трансформации ![]() , обусловленной искажающим воздействием шумов и помех, присутствующих в любом реальном канале. Классическим вопросом теории радиоприема является следующий: что представляет собой наилучшее правило решения о том, какое из возможных сообщений (или сигналов) было передано, если принято наблюдение
, обусловленной искажающим воздействием шумов и помех, присутствующих в любом реальном канале. Классическим вопросом теории радиоприема является следующий: что представляет собой наилучшее правило решения о том, какое из возможных сообщений (или сигналов) было передано, если принято наблюдение ![]() ?
?
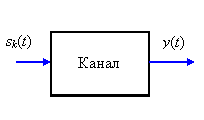
Для ответа на поставленный вопрос необходимо знать модель канала. Математическое описание канала дается переходной вероятностью ![]() , характеризующей вероятность трансформации каналом заданного входного сигнала в то или иное выходное наблюдение
, характеризующей вероятность трансформации каналом заданного входного сигнала в то или иное выходное наблюдение ![]() . Если значения переходной вероятности
. Если значения переходной вероятности ![]() известны для всех возможных пар
известны для всех возможных пар ![]() и
и ![]() , канал исчерпывающе описан.
, канал исчерпывающе описан.
При равной вероятности всех сообщений источника (что, как правило, характерно для разумно спроектированной системы) оптимальной стратегией наблюдателя, обеспечивающей минимальный риск перепутывания действительно переданного сигнала с каким-то другим, является правило максимального правдоподобия (МП). Согласно этому алгоритму по получении колебания ![]() решение принимается в пользу того сигнала, для которого вероятность трансформации каналом именно в наблюдение
решение принимается в пользу того сигнала, для которого вероятность трансформации каналом именно в наблюдение ![]() является наибольшей (в сравнении с другими сигналами).
является наибольшей (в сравнении с другими сигналами).
В теории связи наиболее распространенной моделью служит канал с аддитивным белым гауссовским шумом (АБГШ), или просто гауссовский канал, в котором переходная вероятность экспоненциально уменьшается с ростом квадрата евклидова расстояния между переданным сигналом и выходным наблюдением:
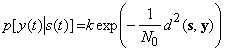 ,
,
где ![]() – константа, не зависящая от
– константа, не зависящая от ![]() и
и ![]() ,
, ![]() – односторонняя спектральная плотность мощности белого шума, а евклидово расстояние между
– односторонняя спектральная плотность мощности белого шума, а евклидово расстояние между ![]() и
и ![]() определяется как
определяется как
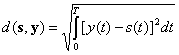
где T – интервал наблюдения.
Очевидно, что правдоподобие сигнала (вероятность того, что именно он преобразован каналом в наблюдение ![]() ) уменьшается с увеличением евклидова расстояния между
) уменьшается с увеличением евклидова расстояния между ![]() и
и ![]() .Следовательно, правило МП для гауссовского канала можно переформулировать как правило минимума расстояния: решение принимается в пользу сигнала
.Следовательно, правило МП для гауссовского канала можно переформулировать как правило минимума расстояния: решение принимается в пользу сигнала ![]() , поскольку он наиболее близок (в смысле евклидова расстояния) к наблюдению
, поскольку он наиболее близок (в смысле евклидова расстояния) к наблюдению ![]() среди всех
среди всех ![]() конкурирующих сигналов.
конкурирующих сигналов.
Часто при отображении сообщений в сигналы выдвигается требование равенства энергии для всех сигналов. В этом случае правило минимума расстояния можно толковать как правило максимума корреляции, означающее, в частности, что среди всех возможных сигналов одинаковой энергии принятым объявляется тот, который имеет наибольшую корреляцию с наблюдением ![]()
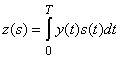 .
.
1.2. Передача двоичных данных

Пусть для передачи одного бита данных используются два различных сигнала ![]() и
и ![]() , отвечающих 0 и 1 соответственно. Тогда правилу минимального расстояния
, отвечающих 0 и 1 соответственно. Тогда правилу минимального расстояния
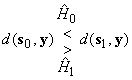 ,
,
где ![]() символизирует, что «решение принято в пользу сигнала с индексом
символизирует, что «решение принято в пользу сигнала с индексом ![]() », может быть дана наглядная геометрическая интерпретация (см. рисунок). Решения
», может быть дана наглядная геометрическая интерпретация (см. рисунок). Решения ![]() и
и ![]() выносятся на основании попадания вектора наблюдения
выносятся на основании попадания вектора наблюдения ![]() в соответствующую половину плоскости, содержащей сигнальные вектора
в соответствующую половину плоскости, содержащей сигнальные вектора ![]() и
и ![]() . Вероятность ошибки, т.е. перепутывания сигналов
. Вероятность ошибки, т.е. перепутывания сигналов ![]() зависит от расстояния
зависит от расстояния ![]() между векторами
между векторами ![]() и
и ![]() отнесенному к диапазону случайных флюктуаций
отнесенному к диапазону случайных флюктуаций ![]() , обусловленных канальным шумом:
, обусловленных канальным шумом:
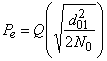 ,
,
где 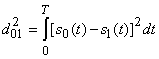 ,
,
а 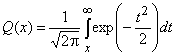 – дополнительная функция ошибок.
– дополнительная функция ошибок.
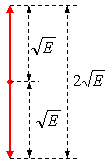
При наложении энергетических ограничений единственным путем достижения высокой достоверности двоичной передачи данных является увеличение расстояния между сигналами. При равенстве энергий обоих сигналов
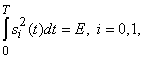
максимум расстояния
![]()
достигается на паре противоположных сигналов
![]() .
.
Бинарная фазовая манипуляция (БФМ) практически реализует подобную пару и широко используется в цифровых системах передачи данных. Вероятность ошибки при передаче двоичных данных посредством БФМ
![]()
![]() ,
,
где
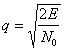
отношение сигнал-шум (ОСШ) на выходе согласованного фильтра.
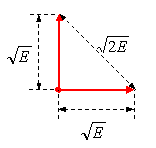
В некоторых случаях требования реализационного плана диктуют применение не оптимальных сигналов, например ортогональную пару, что достигается при бинарной частотной манипуляции (БЧМ). Расстояние между ортогональными сигналами в корень из двух раз меньше, чем для противоположных сигналов (см. рисунок справа) и для ортогональной пары равная с БФМ вероятность ошибки достигается ценой удвоения энергии сигналов относительно БФМ. Иными словами, ортогональные сигналы энергетически проигрывают противоположным 3 дБ.
Еще одно выражение для расстояния оказывается очень продуктивным. Для сигналов с равными энергиями раскрытие скобок в подынтегральном выражении для квадрата расстояния приводит к соотношению
![]() ,
,
где коэффициент корреляции между сигналами
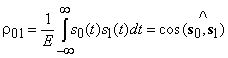
геометрически есть просто косинус угла между сигнальными векторами ![]() и, тем самым, характеризует близость, или сходство сигналов. Для противоположных сигналов (БФМ)
и, тем самым, характеризует близость, или сходство сигналов. Для противоположных сигналов (БФМ) ![]() , тогда как для ортогональных (БЧМ)
, тогда как для ортогональных (БЧМ) ![]() . В любом случае
. В любом случае
![]() .
.
Существует еще один, достаточно старый, способ двоичной передачи: бинарная амплитудная манипуляция (БАМ), называемая также амплитудно-импульсной модуляцией (АИМ). В данной схеме символ ‘0’ передается импульсом с энергией ![]() , а символ ‘1’ – паузой, так что
, а символ ‘1’ – паузой, так что
![]() ,
,
а вероятность ошибки
![]() ,
,
демонстрирующая, что БАМ требует на 6 дБ большей энергии, чем БФМ, для достижения той же достоверности передачи, когда ограничение наложено на пиковую энергию. На практике чаще ограничение накладывается на среднюю энергию, тогда потери БАМ составляют лишь 3 дБ по сравнению с БФМ, т.е. обладают энергетическим проигрышем, что и у БЧМ.
Проведенный анализ дает основание для следующего вывода о роли выбора сигнальной пары для передачи двоичной информации: отсутствует малейший намек на получение каких-либо преимуществ от привлечения широкополосных сигналов, так как расширение полосы сигнала сверх минимума ![]() не приведет к уменьшению вероятности ошибки. Для обеспечения желаемой достоверности приема достаточно лишь применить пару сигналов, максимально удаленных друг от друга, что автоматически предполагает использование противоположных сигналов без дополнительных требований к их форме и модуляции. Если по каким-либо причинам использование противоположной пары нецелесообразно, ни ортогональная (БЧМ), ни БАМ пары сигналов также никоим образом не стимулируют к применению технологии расширения спектра.
не приведет к уменьшению вероятности ошибки. Для обеспечения желаемой достоверности приема достаточно лишь применить пару сигналов, максимально удаленных друг от друга, что автоматически предполагает использование противоположных сигналов без дополнительных требований к их форме и модуляции. Если по каким-либо причинам использование противоположной пары нецелесообразно, ни ортогональная (БЧМ), ни БАМ пары сигналов также никоим образом не стимулируют к применению технологии расширения спектра.
1.3. Передача М-ичных данных
Обратимся к более общему случаю, когда M альтернативных сигналов s1(t), s2(t), …, sM(t) переносят M возможных сообщений по АБГШ каналу. В наиболее типичной ситуации энергии всех сигналов одинаковы
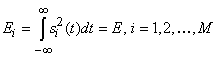 ,
,
что в геометрической интерпретации означает равенство длин всех сигнальных векторов.
Для принятого наблюдения y(t) вычисляются расстояния (или корреляции) между наблюдением и всеми конкурирующими сигналами и решение выносится в пользу того сигнала, который наиболее близок к y(t):
![]() .
.
Для минимизации риска ошибочного решения (т.е. перепутывания одного сигнала с некоторым другим) необходима одновременная максимизация всех расстояний. Однако в данных условиях подобная задача оказывается весьма нетривиальной, поскольку они могут конфликтовать друг с другом: удаление некоторого вектора от соседнего, чревато риском приближения его к какому-то третьему. Можно показать, что минимальное расстояние между любой парой различных сигналов ограничено следующим соотношением
![]() .
.
Следовательно, если вероятность перепутывания ближайших сигналов (максимальная вероятность ошибки) минимизирована, то оптимальными являются сигналы, лежащие нам этой границе. Подобные сигналы, известные под наименованием симплексных, являются эквидистантными и обладают одинаковыми коэффициентами корреляции
![]() .
.
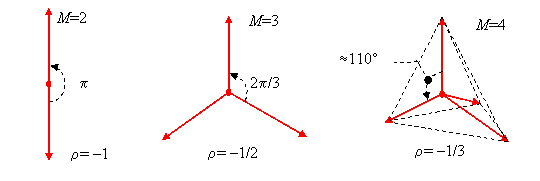 Простейшие множества симплексных сигналов
Простейшие множества симплексных сигналовПри достаточно большом числе сообщений M![]() коэффициент корреляции симплексных сигналов стремится к нулю
коэффициент корреляции симплексных сигналов стремится к нулю ![]() и ортогональные сигналы становятся эквивалентными по помехоустойчивости симплексным. Вероятность ошибки когерентного приема
и ортогональные сигналы становятся эквивалентными по помехоустойчивости симплексным. Вероятность ошибки когерентного приема ![]() ортогональных сигналов может быть вычислена как
ортогональных сигналов может быть вычислена как
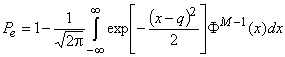 ,
,
где q , как и прежде, отношение сигнал-шум на выходе согласованного фильтра, а
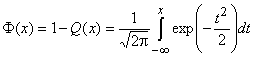
стандартная функция ошибок.
Наряду с точной формулой в инженерной и исследовательской практике применяется иное соотношение для быстрого получения оценки вероятности ошибки. При его выводе используется неравенство, называемое аддитивной границей
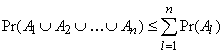
свидетельствующее, что вероятность объединения событий ![]() не превышает суммы их вероятностей. На основании этого
не превышает суммы их вероятностей. На основании этого ![]() может быть оценена сверху суммой вероятностей ошибок различения двух сигналов, приводя к границе объединения для
может быть оценена сверху суммой вероятностей ошибок различения двух сигналов, приводя к границе объединения для ![]() ортогональных сигналов
ортогональных сигналов
![]()
Данная граница обладает высокой надежностью при малой вероятности ошибки ![]() , обеспечивая оценкой, практически не отличающейся от истинного значения. Кроме того, она гарантирует «запас безопасности», поскольку истинное значение вероятности ошибки всегда лежит ниже границы объединения. Это служит объяснением широкой популярности границы объединения.
, обеспечивая оценкой, практически не отличающейся от истинного значения. Кроме того, она гарантирует «запас безопасности», поскольку истинное значение вероятности ошибки всегда лежит ниже границы объединения. Это служит объяснением широкой популярности границы объединения.
1.4. Обмен выигрыша от ортогонального кодирования на ширину полосы
Оценим теперь выигрыш, сопровождающий применение ортогональных сигналов в сравнении с некодированной передачей, т.е. непосредственной передачей потока информационных битов источника. Предположим, что энергетический ресурс позволяет передавать каждый бит данных с энергией ![]() , тогда минимальная величина квадрата расстояния между сигналами, отвечающими неидентичным
, тогда минимальная величина квадрата расстояния между сигналами, отвечающими неидентичным ![]() –битовым блокам, совпадает со значением квадрата расстояния в однобитовой противоположной паре, т.е.
–битовым блокам, совпадает со значением квадрата расстояния в однобитовой противоположной паре, т.е. ![]() .
.
Рассмотрим теперь другую систему, в которой все различные ![]() –битовые блоки передаются ортогональными сигналами. Ясно, что каждый такой сигнал обладает энергией
–битовые блоки передаются ортогональными сигналами. Ясно, что каждый такой сигнал обладает энергией ![]() , при фиксированном значении энергии на бит
, при фиксированном значении энергии на бит ![]() . Тогда квадрат расстояния между сигналами (один и тот же для любой пары сигналов, поскольку ортогональные сигналы эквидистантны) составляет величину
. Тогда квадрат расстояния между сигналами (один и тот же для любой пары сигналов, поскольку ортогональные сигналы эквидистантны) составляет величину ![]() . Следовательно, асимптотический энергетический выигрыш
. Следовательно, асимптотический энергетический выигрыш ![]() ортогональных сигналов в значении минимума квадрата расстояния по сравнению с некодированной передачей составляет
ортогональных сигналов в значении минимума квадрата расстояния по сравнению с некодированной передачей составляет
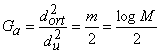 .
.
Термин асимптотический свидетельствует о том, что достоверность оценки достигается при вероятности ошибки, стремящейся к нулю, или, что эквивалентно, при бесконечном ОСШ. При конечной величине отношения сигнал-шум выигрыш становится меньшим, и его значение определяется точными выражениями для вероятности ошибки при некодированной и ортогональной сигнализации.
Рисунок на слайде иллюстрирует зависимость вероятности ошибки от ОСШ при кодировании 10-битовых блоков. Первая кривая (черная линия) представляет вероятность ошибки на блок при некодированной передаче, а две других – ту же вероятность при кодировании 10–битовых блоков ![]() ортогональными сигналами, обрабатываемыми когерентно. Синяя кривая построена на основании аддитивной границы, тогда как красная линия, отвечает точной формуле для вероятности ошибки когерентного приема
ортогональными сигналами, обрабатываемыми когерентно. Синяя кривая построена на основании аддитивной границы, тогда как красная линия, отвечает точной формуле для вероятности ошибки когерентного приема ![]() ортогональных сигналов
ортогональных сигналов
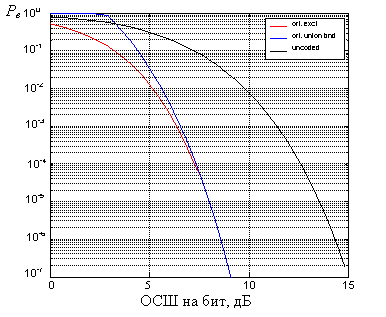
Платой за получение выигрыша ![]() служит расширение полосы, занимаемой ортогональными сигналами. Первоначально отметим, что если все сигналы сосредоточены в пределах полосы
служит расширение полосы, занимаемой ортогональными сигналами. Первоначально отметим, что если все сигналы сосредоточены в пределах полосы ![]() (т.е. отсутствуют спектральные компоненты выше
(т.е. отсутствуют спектральные компоненты выше ![]() ), то отсчеты, взятые с частотой
), то отсчеты, взятые с частотой ![]() , исчерпывающе определяют исходный непрерывный во времени сигнал. В свою очередь это означает, что при длительности сигнала
, исчерпывающе определяют исходный непрерывный во времени сигнал. В свою очередь это означает, что при длительности сигнала ![]() , любой сигнал полностью описывается вектором размерности
, любой сигнал полностью описывается вектором размерности ![]() . Поскольку максимальное число ортогональных векторов в n–мерном векторном пространстве равно n, то максимальное число ортогональных сигналов в ограниченной значениями
. Поскольку максимальное число ортогональных векторов в n–мерном векторном пространстве равно n, то максимальное число ортогональных сигналов в ограниченной значениями ![]() и
и ![]() частотно-временной области составит
частотно-временной области составит
![]() ,
,
иначе говоря, для расположения M сигналов длительности ![]() требуется минимально необходимая полоса, равная
требуется минимально необходимая полоса, равная ![]() .
.
При достаточно большом числе M передаваемых сообщений ![]() полная полоса, необходимая для обеспечения ортогональности сигналов, значительно больше скорости передачи R. Действительно, поскольку
полная полоса, необходимая для обеспечения ортогональности сигналов, значительно больше скорости передачи R. Действительно, поскольку ![]() , то
, то
![]()
При ![]() отношение
отношение ![]() и
и ![]() , экспоненциально возрастая с увеличением выигрыша от кодирования.
, экспоненциально возрастая с увеличением выигрыша от кодирования.
Пример 1.4.1. Предположим, что желательно обеспечить энергетический выигрыш ![]() (4.8 дБ) с помощью ортогонального кодирования. Асимптотически это возможно при
(4.8 дБ) с помощью ортогонального кодирования. Асимптотически это возможно при ![]() в обмен на увеличение полосы (по сравнению со случаем некодированной передачи) в
в обмен на увеличение полосы (по сравнению со случаем некодированной передачи) в ![]() раз. Представим теперь ситуацию, когда, как следствие воодушевления достигнутым, планируется десятикратное (10 дБ) уменьшение излучаемой мощности, кодируя 20-битовые блоки. Это потребует расширения полосы примерно в 50 000 раз, что в большинстве случаев представляется совершенно нереальным.
раз. Представим теперь ситуацию, когда, как следствие воодушевления достигнутым, планируется десятикратное (10 дБ) уменьшение излучаемой мощности, кодируя 20-битовые блоки. Это потребует расширения полосы примерно в 50 000 раз, что в большинстве случаев представляется совершенно нереальным.
Использование достаточно большого M влечет необходимость большого частотно-временного произведения ![]() . Единственно, что это означает, так требование значительности произведения полной (т.е. занимаемой совместно всеми сигналами) полосы и длительности. Данное условие не означает, что
. Единственно, что это означает, так требование значительности произведения полной (т.е. занимаемой совместно всеми сигналами) полосы и длительности. Данное условие не означает, что ![]() должно быть большим, где W и T полоса и длительность одиночного сигнала. Другими словами, ортогональные сигналы необязательно должны реализовывать принцип распределенности спектра. Два первых следующих примера ортогонального кодирования как раз и являются иллюстрацией этого.
должно быть большим, где W и T полоса и длительность одиночного сигнала. Другими словами, ортогональные сигналы необязательно должны реализовывать принцип распределенности спектра. Два первых следующих примера ортогонального кодирования как раз и являются иллюстрацией этого.
1.5. Примеры множеств ортогональных сигналов
Продемонстрируем вначале возможность построения простейших множеств ортогональных сигналов за счет дробления доступного частотно-временного ресурса.
1.5.1. Кодирование временным сдвигом
Этот достаточно тривиальный способ кодирования означает, что каждый из сигналов сдвинут по времени относительно предшествующего на интервал, равный индивидуальной длительности сигнала ![]() . Очевидно, что не перекрывающиеся во временной области сигналы являются ортогональными (см. рисунок):
. Очевидно, что не перекрывающиеся во временной области сигналы являются ортогональными (см. рисунок):
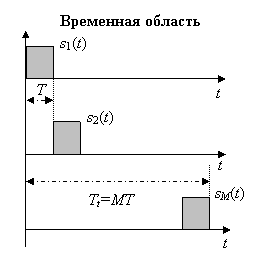
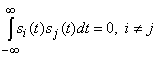
Для каждого индивидуального сигнала частотно-временное произведение ![]() , так что данные сигналы относятся к разряду простых. Недостатки ее, однако, также довольно очевидны и должны соответствующим образом учитываться. Во-первых, необходима точная синхронизация, поскольку флюктуации временного положения сигналов потенциально способны вызвать перекрытие последних, нарушающее их ортогональность. Другим недостатком этого простейшего ортогонального кодирования является то, что для сохранения требуемой энергии каждого сигнала необходимо обеспечить высокую пиковую мощность. Чем выше единицы значение пик-фактора
, так что данные сигналы относятся к разряду простых. Недостатки ее, однако, также довольно очевидны и должны соответствующим образом учитываться. Во-первых, необходима точная синхронизация, поскольку флюктуации временного положения сигналов потенциально способны вызвать перекрытие последних, нарушающее их ортогональность. Другим недостатком этого простейшего ортогонального кодирования является то, что для сохранения требуемой энергии каждого сигнала необходимо обеспечить высокую пиковую мощность. Чем выше единицы значение пик-фактора ![]() (отношения пиковой мощности к средней), тем более жесткие требования предъявляются к линейности усилителя и, как итог, хуже его энергетические показатели. Для временного кодирования
(отношения пиковой мощности к средней), тем более жесткие требования предъявляются к линейности усилителя и, как итог, хуже его энергетические показатели. Для временного кодирования ![]() при
при ![]() .
.
1.5.2. Кодирование частотным сдвигом
Другим прямым способом реализации ортогональности служит кодирование частотным сдвигом. На основании дуальности времени и частоты или теоремы Парсеваля скалярные произведения сигналов ![]() и их спектров
и их спектров ![]() совпадают:
совпадают:
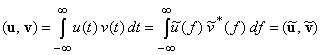 ,
,
что позволяет механически перенести только что обсужденную схему в частотную область (см. рисунок).
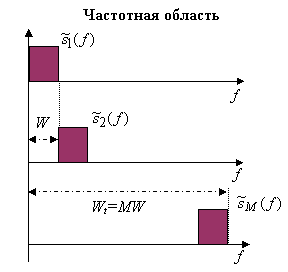
При полном перекрытии сигналов во времени ![]() каждый из них занимает полосу не менее
каждый из них занимает полосу не менее ![]() . Понятно, что каждый индивидуальный сигнал опять не является сигналом с распределенным спектром, поскольку его частотно-временное произведение
. Понятно, что каждый индивидуальный сигнал опять не является сигналом с распределенным спектром, поскольку его частотно-временное произведение ![]() , и значит, любая система со сколь угодно большим числом ортогональных сигналов подобного сорта, конечно, не является системой с распределенным спектром.
, и значит, любая система со сколь угодно большим числом ортогональных сигналов подобного сорта, конечно, не является системой с распределенным спектром.
В отличие от кодирования временным сдвигом пик-фактор ортогональных сигналов данного вида ![]() и ошибки в синхронизации не играют столь критической роли, так как ортогональность достигается отсутствием перекрытия в частотной области. Вместо этого деструктивным в некоторых случаях может оказаться дрейф спектра (к примеру, вследствие эффекта Доплера). Тем не менее данный способ передачи чрезвычайно популярен и примером его непосредственного воплощения служит традиционная
и ошибки в синхронизации не играют столь критической роли, так как ортогональность достигается отсутствием перекрытия в частотной области. Вместо этого деструктивным в некоторых случаях может оказаться дрейф спектра (к примеру, вследствие эффекта Доплера). Тем не менее данный способ передачи чрезвычайно популярен и примером его непосредственного воплощения служит традиционная ![]() -ичная частотная манипуляция.
-ичная частотная манипуляция.
1.5.3. Ортогональное кодирование широкополосными сигналами
Двум ранее рассмотренным методам ортогональной передачи присуще дробление общего частотно-временного ресурса. Первый из них предполагает выделение некоторой части общего временного пространства каждому сигналу, тогда как частотная область совместно используется всеми сигналами. При втором же способе роли временного и частотного пространства меняются местами. Распределение выделенного ресурса при временном и частотном кодировании иллюстрирует ниже приведенный рисунок.
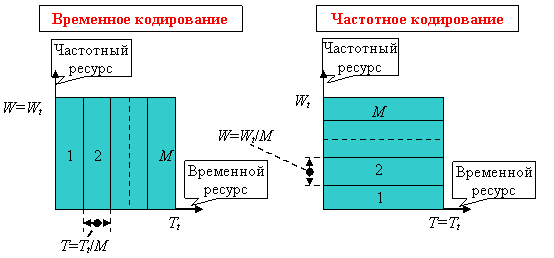
Альтернативой этим простейшим способам кодирования может служить метод, в котором любой сигнал занимает все доступное частотно–временное пространство: ![]() ,
, ![]() , вследствие чего все сигналы являются широкополосными, поскольку
, вследствие чего все сигналы являются широкополосными, поскольку
![]() .
.
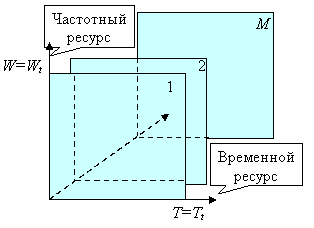
В этих условиях все сигналы совместно используют общий частотно-временной ресурс без распределения или дробления последнего (см. рисунок, на котором третья ось используется для нумерации сигналов).

Рассмотрим простой пример воплощения подобной идеи в форме дискретных БФМ сигналов. Образуем каждый из ![]() сигналов как последовательность
сигналов как последовательность ![]() следующих друг за другом элементарных импульсов или чипов прямоугольной формы и длительности
следующих друг за другом элементарных импульсов или чипов прямоугольной формы и длительности ![]() с изменяющейся полярностью. Предположим использование таких законов чередования полярности чипов, что все сигналы оказываются ортогональными, как это имеет место в примере для M=4 на рисунке слева.
с изменяющейся полярностью. Предположим использование таких законов чередования полярности чипов, что все сигналы оказываются ортогональными, как это имеет место в примере для M=4 на рисунке слева.
При ![]() нахождение законов чередования полярностей, обеспечивающих ортогональность сигналов, эквивалентно нахождению матрицы Адамара. Последняя является матрицей порядка M, состоящей только из элементов
нахождение законов чередования полярностей, обеспечивающих ортогональность сигналов, эквивалентно нахождению матрицы Адамара. Последняя является матрицей порядка M, состоящей только из элементов ![]() и обладающей ортогональными строками. Примеры матриц Адамара порядка два и четыре представлены ниже:
и обладающей ортогональными строками. Примеры матриц Адамара порядка два и четыре представлены ниже:
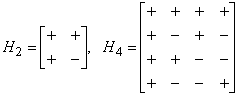 .
.
Достаточно мощным способом конструирования матриц Адамара служит рекуррентный алгоритм Сильвестра, позволяющий построить матрицу порядка ![]() , если уже была найдена матрица порядка
, если уже была найдена матрица порядка ![]() :
:
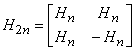 .
.
Не трудно заметить, что, начиная алгоритм Сильвестра с простейшей матрицы ![]() , можно построить матрицы порядка
, можно построить матрицы порядка ![]() , строками которых являются функции Уолша.
, строками которых являются функции Уолша.
Ортогональные сигналы подобного типа лишены недостатков присущих сигналам, ортогональность которых обеспечивается временным или частотным кодированием. Они характеризуются пик-фактором, равным единице, и не требуют параллельных полосовых фильтров в приемнике. Относясь к широкополосным сигналам, они обладают всеми достоинствами широкополосной философии, которые будут рассмотрены позднее. Вследствие этого в настоящее время они находят широкое применение. Так следует упомянуть CDMA систему мобильного телефона 2-го поколения стандарта IS-95 (cdmaOne), в которой используются M=64 функции Уолша как в прямом (для образования каналов), так и в обратном (для рассмотренной выше 64-ичной передачи) каналах. В стандартах мобильной связи 3-го поколения WCDMA и cdma2000 планируется использовать значительно большее число (вплоть до 512) ортогональных сигналов на основе матриц Адамара.
Можно дать следующее резюме к содержанию параграфов 1.3-1.5. Как можно видеть, теоретически классическая задача ![]() -ичной передачи не ориентирует на безоговорочное использование технологии расширения спектра и, в принципе, оптимальный
-ичной передачи не ориентирует на безоговорочное использование технологии расширения спектра и, в принципе, оптимальный ![]() -ичный ансамбль можно составить из простых сигналов. С другой стороны, существуют стимулы реализационного порядка, подкрепленные стремлением к утилизации преимуществ расширенного спектра вне классической постановки задачи приема. Поскольку такая возможность потенциально присутствует всякий раз, когда полный частотно-временной ресурс
-ичный ансамбль можно составить из простых сигналов. С другой стороны, существуют стимулы реализационного порядка, подкрепленные стремлением к утилизации преимуществ расширенного спектра вне классической постановки задачи приема. Поскольку такая возможность потенциально присутствует всякий раз, когда полный частотно-временной ресурс ![]() принципиально необходим, предпочтение разработчиком широкополосных сигналов простым в подобных обстоятельствах может оказаться вполне оправданным.
принципиально необходим, предпочтение разработчиком широкополосных сигналов простым в подобных обстоятельствах может оказаться вполне оправданным.

