14.3.5. Стандарт шифрования данных
Для последовательностей шифрованного текста, размер которых больше расстояния единственности, любая система уравнений (определяющая ключ) может быть решена путем простого перебора всех возможных ключей, пока не будет получено единственное решение. Однако это совершенно непрактично, за исключением применения очень короткого ключа. Например, для ключа, полученного путем перестановки английского алфавита, существует 26!=4
1026 возможных перестановок (в криптографическом смысле это считается малым). Будем считать, что в результате изнурительных поисков мы нашли правильный ключ, перебрав приблизительно половину возможных комбинаций. Если допустить, что каждая проверка потребует для вычисления 1 мкс, то полное время поиска превысит 1012 лет. Следовательно, если криптоаналитик хочет иметь некоторую надежду на успех, то о «лобовых» методах перебора, следует забыть и применять какую-ту иную технологию (например, статистический анализ).
14.3.1. Смешение и диффузия
При расшифровке многих систем шифрования может применяться статистический анализ, использующий частоту появления отдельных символов и их комбинаций. Шеннон [5] предложил две концепции шифрования, усложняющие задачу криптоаналитика. Он назвал эти преобразования «смешение» (confusion) и «диффузия» (diffusion). Смешение — это подстановки, которые делают взаимосвязь между ключом и шифрованным текстом как можно более сложной. Это усложняет применение статистического анализа, сужающего поиск практического подмножества области ключей. В результате смешения дешифрование даже очень короткой последовательности шифрованного текста требует большого числа ключей. Диффузия — это преобразования, сглаживающие статистические различия между символами и их комбинациями. Примером диффузии 26-буквенного алфавита является преобразование последовательности сообщений М=М0, M1, ... в новую последовательность сообщений Y=Y0, Y1, ... с помощью следующего соотношения.
по модулю 26 (14.20)
Здесь каждый символ в последовательности рассматривается как число по модулю 26, s — некоторое выбранное целое число и n = 1, 2, .... Новое сообщение Y будет иметь ту же избыточность, что и исходное сообщение М, но частота появления всех букв в Y будет более равномерной, чем в M. В результате, чтобы статистический анализ принес криптоаналитику какую-либо пользу, ему необходимо перехватить большую последовательность шифрованного текста.
14.3.2. Подстановка
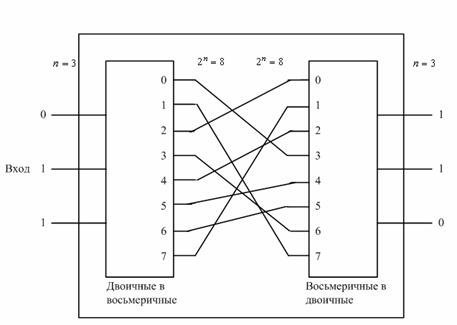
Технология шифрования с помощью подстановки, например использование шифра Цезаря и прогрессивного ключа шифрования Тритемиуса, широко используется в головоломках. Такие простые подстановочные шифры дают малую защищенность. Чтобы к подстановочной технологии можно было применить концепцию смешения, требуется более сложное соотношение. На рис. 14.6 изображен пример создания большей подстановочной сложности с помощью использования нелинейного преобразования. В общем случае п входных битов сначала представляются как один из 2n различных символов (на приведенном рисунке п=2). Затем множество из 2n символов перемешивается так, чтобы каждый символ заменялся другим символом множества. После этого символ снова превращается в n-битовый.
Можно легко показать, что существует (2n)! различные подстановки или связанные с ними возможные модели. Задача криптоаналитика становится вычислительно невозможной для больших n. Пусть п = 128, тогда 2n = 1038 и (2n)! представляет собой астрономическое число. Видим, что для n = 128 это преобразование с помощью блока подстановки (substitution block, S-блок) является сложным (запутывающим). Впрочем, хотя S-блок с п=128 можно считать идеальным, его реализация является невозможной, поскольку она потребует блока с 2n = 1038 контактами.
|
Вход |
000 |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
|
Выход |
011 |
111 |
000 |
110 |
010 |
100 |
101 |
001 |
Рис. 14.6. Блок подстановки
Чтобы убедиться, что S-блок, приведенный на рис. 14.6, представляет собой нелинейное преобразование, достаточно использовать теорему о суперпозиции, которая формулируется ниже. Предположим, что
С = Та + Tb (14.21)
С’ = Т(а + b),
где а и b — входные элементы, С и С' - выходные элементы, а Т - преобразование. Тогда
Если T линейно, С = С’ для всех входных элементов.
Если Т нелинейно, С
С.
Предположим, а = 001 и b = 010; тогда, используя преобразование Т, показанное на рис. 14.6, получим следующее.
С = T(001)
Т(010) = 111000 = 111
С = T(001010) = T(011) = 110
Здесь символ обозначает сложение по модулю 2. Поскольку СС, S-блок является нелинейным.
14.3.3. Перестановка
При перестановке (транспозиции) буквы исходного открытого текста в сообщении не заменяются другими буквами алфавита, как в классических шифрах, а просто переставляются. Например, слово «THINK» после перестановки может выглядеть как шифрованный текст HKTNL. На рис. 14.7 приведен пример бинарной перестановки данных (линейная операция). Видно, что входные данные, просто перемешиваются или переставляются. Преобразование выполняется с помощью блока перестановки (permutation block, Р-блок). Технология, используемая сама по себе, имеет один основной недостаток: она уязвима по отношению к обманным сообщениям. Обманное сообщение изображено на рис. 14.7. Подача на вход единственной 1 (при остальных 0) позволяет обнаружить одну из внутренних связей. Если криптоаналитику необходимо выполнить криптоанализ такой системы с помощью атаки открытого текста, он отправит последовательность таких обманных сообщений, при каждой передаче смещая единственную 1 на одну позицию. Таким образом, обнаруживаются все связи входа и выхода. Данный пример показывает, почему защищенность системы не должна зависеть от ее архитектуры.
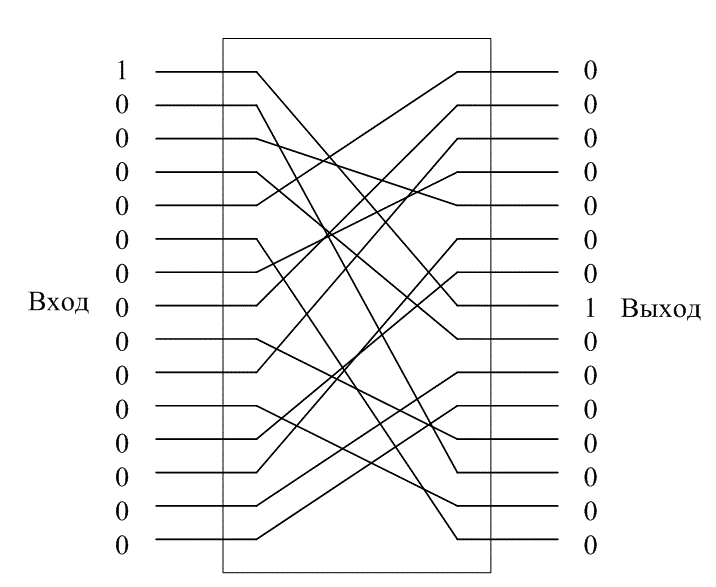
Рис. 14.7. Блок перестановки
14.3.4. Продукционный шифр
Для преобразований, включающих значительное число n-символьных сообщений, желательным является применение обеих описанных выше схем (S-блока и Р-блока). Шеннон [5] предложил использовать продукционный шифр, или комбинацию преобразований S- и Р-блоков, которые вместе могут дать более мощную систему шифрования, чем каждый из них в отдельности. Этот подход, выборочно использующий преобразования замещения и перестановки, был использован IBM в системе LUCIFER [7, 8] и стал основой национального стандарта шифрования данных (Data Encryption Standard — DES) [9]. На рис. 14.8 изображены такие комбинации Р- и S-блоков. Дешифрование выполняется обратным прогоном данных, при котором используются преобразования, обратные к преобразованию каждого S -блока. Систему, изображенную на рис. 14.8, реализовать довольно трудно, поскольку все S -блоки являются различными, случайно генерируемый ключ неприменим и система не дает возможности повторить одну и ту же последовательность операций. Поэтому в системе LUCIFER [8] использовались два различных типа S -блоков, S1 и S0, которые могли быть общедоступными. Пример такой системы изображен на рис. 14.9. Входные данные преобразуются с помощью последовательности S- и Р-блоков, определяемой ключом. В приведенном примере ключ размером 25 бит определяет, какой из двух блоков (S1 или S0) следует выбрать на каждой из 25 позиций схемы. Таким образом, подробности аппарата шифрования могут быть открыты, поскольку защищенность системы обеспечивается ключом.
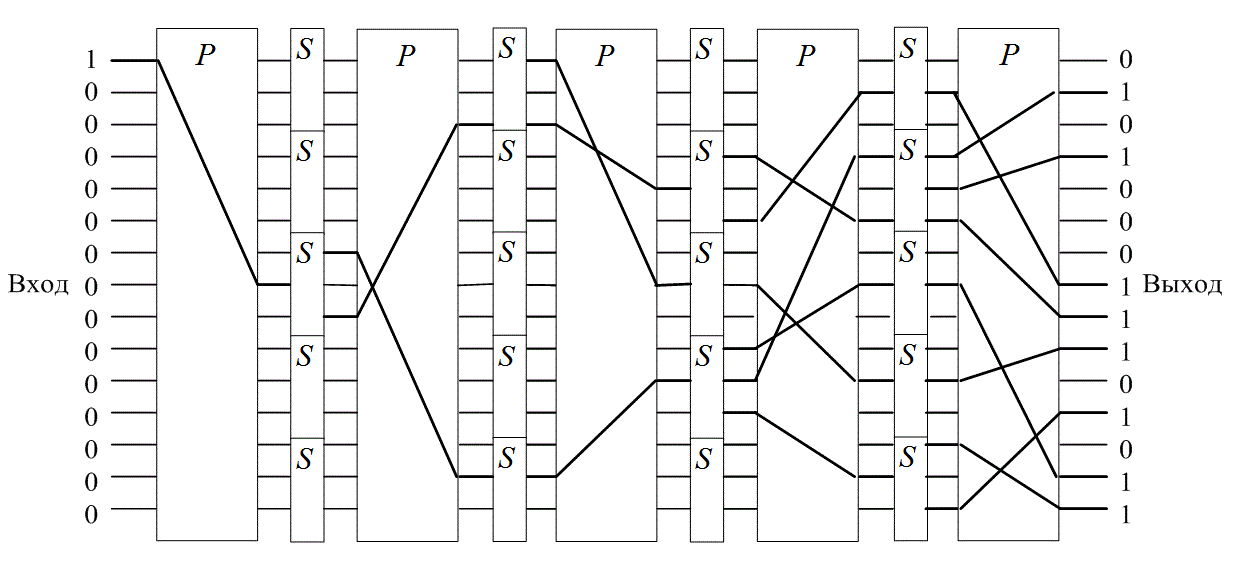
Рис. 14.8. Продукционная система шифрования
Рис. 14.9. Индивидуальные возможности, определяемые ключом
Итеративная структура продукционной системы шифрования (рис. 14.9) является типичной для большинства реальных блочных шифров. Сообщения делятся на последовательные блоки по n бит, каждый из которых шифруется одним и тем же ключом, n-битовый блок представляет один из 2n различных символов, допускающих (2n)! различные схемы подстановки. Следовательно, чтобы реализация схемы была разумной, подстановочная часть шифрования выполняется параллельно на небольших сегментах блока. Пример подобной схемы рассмотрен в следующем разделе.
14.3.5. Стандарт шифрования данных
В 1977 году Национальное бюро стандартов США (National Bureau of Standards) приняло модифицированную систему LUCIFER в качестве Национального стандарта шифрования данных (Data Encryption Standard — DES) [9]. Как показано на рис. 14.10, с точки зрения системы ввода-вывода DES может считаться блочной системой шифрования с алфавитом в 264 символа. Входной блок из 64 бит, который является в этом алфавите символом открытого текста, заменяется новым символом шифрованного текста. На рис. 14.11 в виде блочной диаграммы показаны функции системы. Алгоритм шифрования начинается с начальной перестановки 64 бит открытого текста, описанной в таблице начальной перестановки (табл. 14.1). Таблица начальной перестановки читается слева направо и сверху вниз, так что после перестановки биты x1, х2, ..., х64 превращаются в х58, x50, ..., х7. После этой начальной перестановки начинается основная часть алгоритма шифрования, состоящая из 16 итераций, которые используют стандартный блок, показанный на рис. 14.12. Для преобразования 64 бит входных данных в 64 бит выходных, определенных как 32 бит левой половины и 32 бит правой, стандартный блок использует 48 бит ключа. Выход каждого стандартного блока становится входом следующего стандартного блока. Входные 32 бит правой половины (Ri-1) без изменений подаются на выход и становятся 32 бит левой половины (Li). Эти Ri-1 бит с помощью таблицы расширения (табл. 14.2) также расширяются и преобразуются в 48 бит, после чего суммируются по модулю 2 с 48 бит ключа. Как и в случае таблицы начальной перестановки, таблица расширения читается слева направо и сверху вниз.
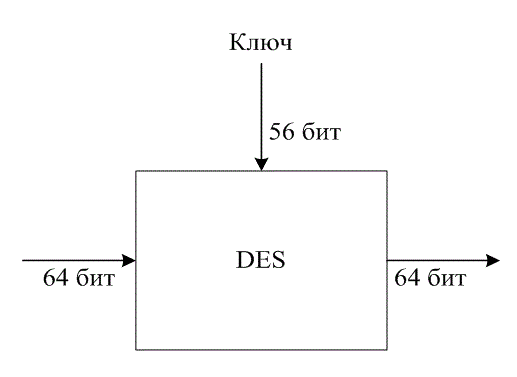
Рис. 14.10. Стандарт шифрования данных (DES) в виде блочной системы шифрования
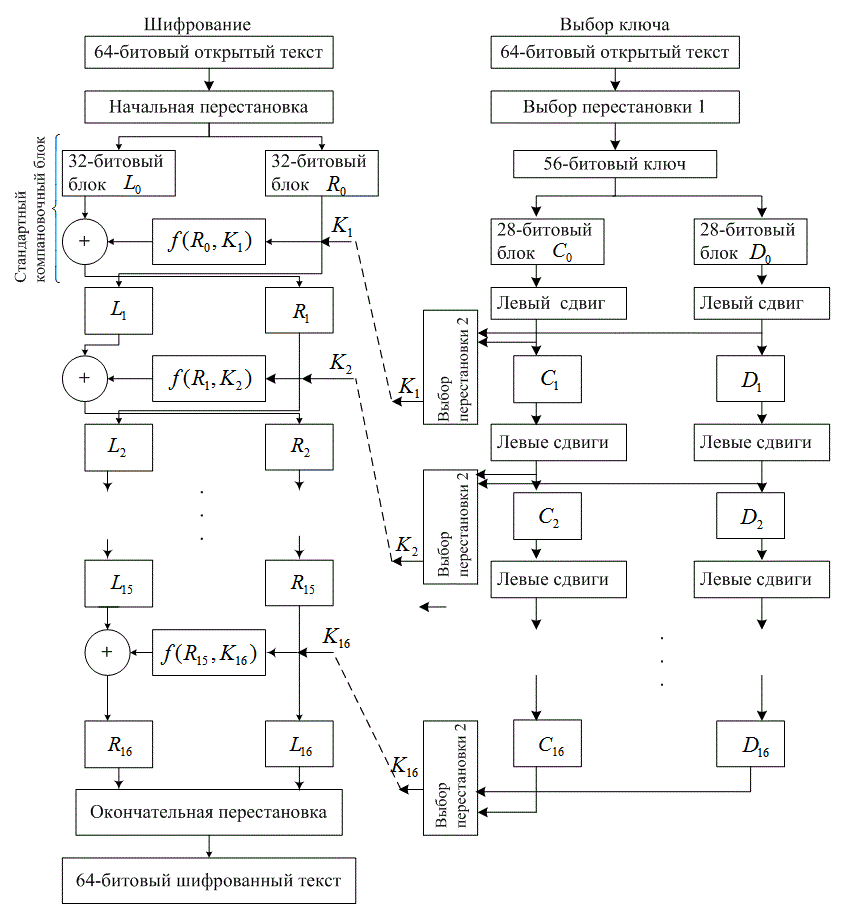
Рис. 14.11. Стандарт шифрования данных
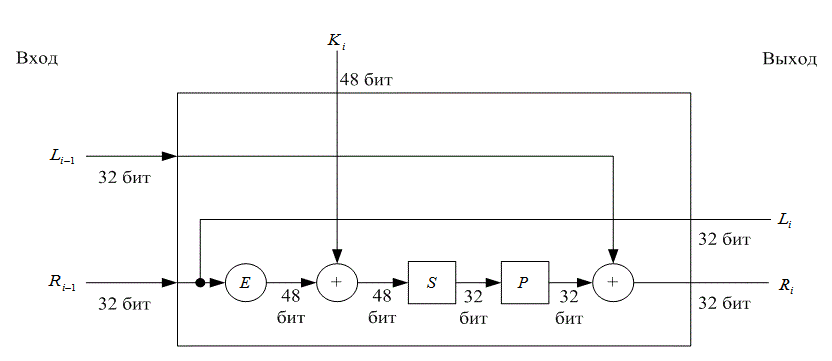
Рис. 14.12. Стандартный компоновочный блок
Данная таблица отображает биты
Таблица 14.1. Начальная перестановка
|
58 |
50 |
42 |
34 |
26 |
18 |
10 |
2 |
|
60 |
52 |
44 |
36 |
28 |
20 |
12 |
4 |
|
62 |
54 |
46 |
38 |
30 |
22 |
14 |
6 |
|
64 |
56 |
48 |
40 |
32 |
24 |
16 |
8 |
|
57 |
49 |
41 |
33 |
25 |
17 |
9 |
1 |
|
59 |
51 |
43 |
35 |
27 |
19 |
11 |
3 |
|
61 |
53 |
45 |
37 |
29 |
21 |
13 |
5 |
|
63 |
55 |
47 |
39 |
31 |
23 |
15 |
7 |
Таблица 14.2. Таблица выбора бит
|
32 |
1 |
2 |
3 |
4 |
5 |
|
4 |
5 |
6 |
7 |
8 |
9 |
|
8 |
9 |
10 |
11 |
12 |
13 |
|
12 |
13 |
14 |
15 |
16 |
17 |
|
16 |
17 |
18 |
19 |
20 |
21 |
|
20 |
21 |
12 |
23 |
24 |
25 |
|
24 |
25 |
26 |
27 |
28 |
29 |
|
28 |
29 |
30 |
31 |
32 |
1 |
Ri-1 = x1, x2, …, x32
в биты
(Ri-1)E = x32, …, x1, x2, …, x32, x1. (14.22)
Отметим, что биты, обозначенные в первом и последнем столбцах таблицы расширения, — это те битовые разряды, которые дважды использовались для расширения из 32 до 48 бит.
Далее (Ri-1)E суммируется по модулю 2 с i-м ключом, выбор которого описывается позднее, а результат разделяется на восемь 6-битовых блоков.
B1, B2, …, B8
Иными словами,
(Ri-1)E Ki = B1, B2, …, B8 (14.23)
Каждый из восьми 6-битовых блоков Bj используется как вход функции S-блока, возвращающей 4-битовый блок Sj(Bj)). Таким образом, входные 48 бит с помощью функции S-блока преобразуются в 32 бит. Функция отображения S-блока Sj определена в табл. 14.3. Преобразование Вj=b1, b2, b3, b4, b5, b6, выполняется следующим образом. Нужная строка — это b1b6, а нужный столбец — b2b3b4b5. Например, если b1= 110001, то преобразование Si возвращает значение из строки 3, столбца 8, т.е. число 5 (в двоичной записи 0101). 32-битовый блок, полученный на выходе S-блока, переставляется с использованием таблицы перестановки (табл. 14.4). Как и другие таблицы, Р-таблица читается слева направо и сверху вниз, так что в результате перестановки битов х1, х2,..., х32 получаем х16, х7,..., х25. 32-битовый выход Р-таблицы суммируется по модулю 2 с 32 бит левой половины (Li-1), образуя выходные 32 бит правой половины (Ri).
Таблица 14.3. Функции выбора S-блока
|
Столбец |
|||||||||||||||||
|
Строка |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
0 |
14 |
4 |
13 |
1 |
2 |
15 |
11 |
8 |
3 |
10 |
6 |
12 |
5 |
9 |
0 |
7 |
|
|
1 |
0 |
15 |
7 |
4 |
14 |
2 |
13 |
1 |
10 |
6 |
12 |
11 |
9 |
5 |
3 |
8 |
|
|
2 |
4 |
1 |
14 |
8 |
13 |
6 |
2 |
11 |
15 |
12 |
9 |
7 |
3 |
10 |
5 |
0 |
S1 |
|
3 |
15 |
12 |
8 |
2 |
4 |
9 |
1 |
7 |
5 |
11 |
3 |
14 |
10 |
0 |
6 |
13 |
|
|
0 |
15 |
1 |
8 |
14 |
6 |
11 |
3 |
4 |
9 |
7 |
2 |
13 |
12 |
0 |
5 |
10 |
|
|
1 |
3 |
13 |
4 |
7 |
15 |
2 |
8 |
14 |
12 |
0 |
1 |
10 |
6 |
9 |
11 |
5 |
|
|
2 |
0 |
14 |
7 |
11 |
10 |
4 |
13 |
1 |
5 |
8 |
12 |
6 |
9 |
3 |
2 |
15 |
S2 |
|
3 |
13 |
8 |
10 |
1 |
3 |
15 |
4 |
2 |
11 |
6 |
7 |
12 |
0 |
5 |
14 |
9 |
|
|
0 |
10 |
0 |
9 |
14 |
6 |
3 |
15 |
5 |
1 |
13 |
12 |
7 |
11 |
4 |
2 |
8 |
|
|
1 |
13 |
7 |
0 |
9 |
3 |
4 |
6 |
10 |
2 |
8 |
5 |
14 |
12 |
11 |
15 |
1 |
|
|
2 |
13 |
6 |
4 |
9 |
8 |
15 |
3 |
0 |
11 |
1 |
2 |
12 |
5 |
10 |
14 |
7 |
S3 |
|
3 |
1 |
10 |
13 |
0 |
6 |
9 |
8 |
7 |
4 |
15 |
14 |
3 |
11 |
5 |
2 |
12 |
|
|
0 |
7 |
13 |
14 |
3 |
0 |
6 |
9 |
10 |
1 |
2 |
8 |
5 |
11 |
12 |
4 |
15 |
|
|
1 |
13 |
8 |
11 |
5 |
6 |
15 |
0 |
3 |
4 |
7 |
2 |
12 |
1 |
10 |
14 |
9 |
|
|
2 |
10 |
6 |
9 |
0 |
12 |
11 |
7 |
13 |
15 |
1 |
3 |
14 |
5 |
2 |
8 |
4 |
S4 |
|
3 |
3 |
15 |
0 |
6 |
10 |
1 |
13 |
8 |
9 |
4 |
5 |
11 |
12 |
7 |
2 |
14 |
|
|
0 |
2 |
12 |
4 |
1 |
7 |
10 |
11 |
6 |
8 |
5 |
3 |
15 |
13 |
0 |
14 |
9 |
|
|
1 |
14 |
11 |
2 |
12 |
4 |
7 |
13 |
1 |
5 |
0 |
15 |
10 |
3 |
9 |
8 |
6 |
|
|
2 |
4 |
2 |
1 |
11 |
10 |
13 |
7 |
8 |
15 |
9 |
12 |
5 |
6 |
3 |
0 |
14 |
S5 |
|
3 |
11 |
8 |
12 |
7 |
1 |
14 |
2 |
13 |
6 |
15 |
0 |
9 |
10 |
4 |
5 |
3 |
|
|
0 |
12 |
1 |
10 |
15 |
9 |
2 |
6 |
8 |
0 |
13 |
3 |
4 |
14 |
7 |
5 |
11 |
|
|
1 |
10 |
15 |
4 |
2 |
7 |
12 |
9 |
5 |
6 |
1 |
13 |
14 |
0 |
11 |
3 |
8 |
|
|
2 |
9 |
14 |
15 |
5 |
2 |
8 |
12 |
3 |
7 |
0 |
4 |
10 |
1 |
13 |
11 |
6 |
S6 |
|
3 |
4 |
3 |
2 |
12 |
9 |
5 |
15 |
0 |
11 |
14 |
1 |
7 |
6 |
0 |
8 |
13 |
|
|
0 |
4 |
11 |
2 |
14 |
15 |
0 |
8 |
13 |
3 |
12 |
9 |
7 |
5 |
10 |
6 |
1 |
|
|
1 |
13 |
0 |
11 |
7 |
4 |
9 |
1 |
10 |
14 |
3 |
5 |
12 |
2 |
15 |
8 |
6 |
|
|
2 |
1 |
4 |
11 |
13 |
12 |
3 |
7 |
14 |
10 |
15 |
6 |
8 |
0 |
5 |
9 |
2 |
S7 |
|
3 |
6 |
11 |
13 |
8 |
1 |
4 |
10 |
7 |
9 |
5 |
0 |
15 |
14 |
2 |
3 |
12 |
|
|
0 |
13 |
2 |
8 |
4 |
6 |
15 |
11 |
1 |
10 |
9 |
3 |
14 |
5 |
0 |
12 |
7 |
|
|
1 |
1 |
15 |
13 |
8 |
10 |
3 |
7 |
4 |
12 |
5 |
6 |
11 |
0 |
14 |
9 |
2 |
|
|
2 |
7 |
11 |
4 |
1 |
9 |
12 |
14 |
2 |
0 |
6 |
10 |
13 |
15 |
3 |
5 |
8 |
S8 |
|
3 |
2 |
1 |
14 |
7 |
4 |
10 |
8 |
13 |
15 |
12 |
9 |
0 |
3 |
5 |
6 |
11 |
|
Таблица 14.4. Таблица перестановки
|
16 |
7 |
20 |
21 |
|
29 |
12 |
28 |
17 |
|
1 |
15 |
23 |
26 |
|
5 |
18 |
31 |
10 |
|
2 |
8 |
24 |
14 |
|
32 |
27 |
3 |
9 |
|
19 |
13 |
30 |
6 |
|
22 |
11 |
4 |
25 |
Алгоритм стандартного блока может быть представлен следующим образом.
Li = Ri-1 (14.24)
Ri = Li-1f (Ri-1,Ki) (14.25)
Здесь f (Ri-1,Ki) обозначает функциональное соотношение, включающее описанные выше расширение, преобразование в S-блоке и перестановку. После 16 итераций в таких стандартных блоках данные размещаются согласно окончательной обратной перестановке, описанной в табл. 14.5, где, как и ранее, выходные биты читаются слева направо и сверху вниз.
Таблица 14.5. Окончательная перестановка
|
40 |
8 |
48 |
16 |
56 |
24 |
64 |
32 |
|
39 |
7 |
47 |
15 |
55 |
23 |
63 |
31 |
|
38 |
6 |
46 |
14 |
54 |
22 |
62 |
30 |
|
37 |
5 |
45 |
13 |
53 |
21 |
61 |
29 |
|
36 |
4 |
44 |
12 |
52 |
20 |
60 |
28 |
|
35 |
3 |
43 |
11 |
51 |
19 |
59 |
27 |
|
34 |
2 |
42 |
10 |
50 |
18 |
58 |
26 |
|
33 |
1 |
41 |
9 |
49 |
17 |
57 |
25 |
Для дешифрования применяется тот же алгоритм, но ключевая последовательность, используемая в стандартном блоке, берется в обратном порядке. Отметим, что значение f(Ri-1, Ki), которое может быть также выражено через выход i-ro блока как f(Li, Ki), делает процесс дешифрования возможным.
14.3.5.1. Выбор ключа
Выбор ключа также происходит в течение 16 итераций, как показано в соответствующей части рис. 14.11. Входной ключ состоит из 64-битового блока с 8 бит четности в разрядах 8, 16..... 64. Перестановочный выбор 1 отбрасывает биты четности и переставляет оставшиеся 56 бит согласно табл. 14.6. Выход данной процедуры делится пополам на два элемента — С и D, каждый из которых состоит из 28 бит. Выбор ключа проходит за 16 итераций, проводимых для создания различных множеств 48 ключевых бит для каждой итерации шифрования. Блоки С и D последовательно сдвигаются согласно следующим выражениям.
Таблица 14.6. Круговая перестановка
|
57 |
49 |
41 |
33 |
25 |
17 |
9 |
|
1 |
58 |
50 |
42 |
14 |
26 |
18 |
|
10 |
2 |
59 |
51 |
43 |
35 |
27 |
|
19 |
11 |
3 |
60 |
52 |
44 |
36 |
|
63 |
55 |
47 |
39 |
31 |
23 |
15 |
|
7 |
62 |
54 |
46 |
38 |
30 |
22 |
|
14 |
6 |
61 |
53 |
45 |
37 |
29 |
|
21 |
13 |
5 |
28 |
20 |
12 |
4 |
Ci = LSi(Ci-1) и Di = LSi(Di-1) (14.26)
Здесь LSi - левый циклический сдвиг на число позиций, показанных в табл. 14.7. Затем последовательность Ci, Di переставляется согласно перестановочному выбору 2, показанному в табл. 14.8. Результатом является ключевая последовательность Ki, которая используется в i-й итерации алгоритма шифрования.
Таблица 14.7. Ключевая последовательность сдвигов влево
|
Итерация i |
Количество сдвигов влево |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
1 1 2 2 2 2 2 2 1 2 2 2 2 2 2 1 |
Таблица 14.8. Ключевая перестановка 2
|
14 |
17 |
11 |
24 |
1 |
5 |
|
3 |
28 |
15 |
6 |
21 |
10 |
|
23 |
19 |
12 |
4 |
26 |
8 |
|
16 |
7 |
27 |
20 |
13 |
2 |
|
41 |
52 |
31 |
37 |
47 |
55 |
|
30 |
40 |
51 |
45 |
33 |
48 |
|
44 |
49 |
39 |
56 |
34 |
53 |
|
46 |
42 |
50 |
36 |
29 |
32 |
DES может реализовываться подобно блочной системе шифрования (см. рис. 14.11), что иногда называют методом шифровальной книги. Основным недостатком этого метода является то, что (при использовании одного ключа) данный блок входного открытого текста будет всегда давать тот же выходной шифрованный блок. Еще один способ шифрования, называемый способом шифрования с обратной связью, приводит к шифрованию отдельных битов, а не символов, что дает поточное шифрование [3]. В системе шифрования с обратной связью (описанной ниже) шифрование сегмента открытого текста зависит не только от ключа и текущих данных, но и от некоторых предшествующих данных.
С конца 1970-х широко обсуждались два спорных момента, связанных с DES [10]. Первый касается длины ключа. Некоторые исследователи считали, что 56 бит не достаточно, чтобы исключить взлом путем перебора. Второй момент касается внутренней структуры S-блоков, которые никогда не выпускались IBM. Агентство национальной безопасности США, которое было привлечено к тестированию алгоритма DES, потребовало, чтобы эта информация не обсуждалась публично. Критики опасаются, что АНБ участвовало в проектировании этих схем и теперь способно «проникать» в любое сообщение, шифрованное согласно DES [10]. В настоящее время стандарт DES больше не является приемлемым выбором, обеспечивающим надежное шифрование. Поиск 56-битового ключа с помощью недорогих компьютерных методов является делом нескольких дней [11].