Основная трудность вычисления ДПФ при длинных последовательностях заключается в большом количестве арифметических операций, что требует высокого быстродействия вычислительных средств и значительного времени обработки. Так например, для определения спектра последовательности длиной в соответствии с (8.16) требуется комплексных умножений и комплексных сложений. Это в ряде случаев делает затруднительной обработку сигнала в реальном масштабе времени. Быстрое преобразование Фурье (БПФ) позволяет сократить число арифметических операций на несколько порядков.

Основная идея БПФ заключается в разбиении последовательности на подпоследовательности, вычислении ДПФ для каждой из них и объединении результатов вычислений. Наиболее просто алгоритм БПФ реализуется в случае , где – натуральное число. Если , то последовательность дополняется нулями.

Рассмотрим процедуру БПФ на примере деления последовательности на две подпоследовательности. Будем полагать, что в первую подпоследовательность входят значения с четными, а во вторую – с нечетными номерами. Тогда выражение (8.16) принимает вид

. (8.23)

Введем следующие обозначения: подпоследовательность с четными номерами обозначим через , а с нечетными номерами – через . Тогда выражение (8.23) принимает вид

, (8.24)

– четные – нечетные

где .

Но первая сумма в (8.24) представляет собой ДПФ подпоследовательности отсчетов с четными номерами

,

а вторая сумма – ДПФ подпоследовательности отсчетов с нечетными номерами:

.

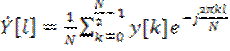Тогда вместо (8.24) получаем выражение

, при . (8.25)

При в силу периодичности спектра дискретной последовательности

, при . (8.26)

Выражения (8.25) и (8.26) представляют собой алгоритм БПФ. Вычислительная схема БПФ может быть представлена в следующем виде (рис. 8.4).

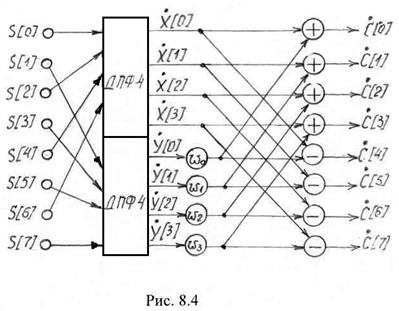
Нетрудно убедиться, что число операций для вычисления сокращается приблизительно в два раза. Если провести дальнейшее разбиение подпоследовательностей и на более короткие подпоследовательности и использовать алгоритм БПФ, аналогичный рассмотренному, то можно добиться еще большего сокращения числа операций.