1.1. Определители (детерминанты)
Обозначения определителя матрицы А: D , det A,![]() .
.
Определитель второго порядка: 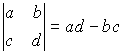 .
.
Определитель третьего порядка:
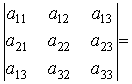
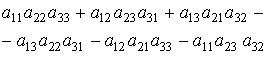
Разложение определителя n-го порядка по i-й строке: 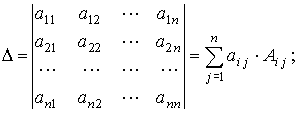
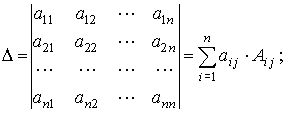
Разложение определителя n-го порядка по j-ому столбцу:
![]() -алгебраическое дополнение элемента
-алгебраическое дополнение элемента ![]() ,
, ![]() ,
,
![]() -минор элемента
-минор элемента ![]() , т.е. определитель, получаемый из исходного определителя вычёркиванием i-й строки и j-го столбца.
, т.е. определитель, получаемый из исходного определителя вычёркиванием i-й строки и j-го столбца.
1.2. Матрицы
| Матрица размерами n x m (n строк и m столбцов): | 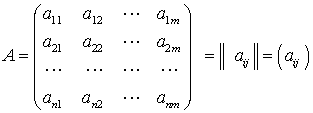 , ,
где |
Равенство матриц: ![]() , если эти матрицы одного размера и
, если эти матрицы одного размера и ![]() .
.
Квадратная матрица порядка n: ![]() .
.
Сложение матриц: ![]() , где
, где ![]() .
.
Свойства сложения матриц:
1) ассоциативность: ![]() ;
;
2) коммутативность: ![]() ;
;
Умножение матрицы на число: ![]() .
.
Умножение матриц: 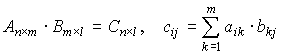 .
.
Свойства умножения матриц:
-
- ассоциативность:
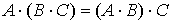 ;
; - некоммутативность.
- определитель произведения квадратных матриц:
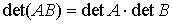 .
.
- ассоциативность:
Транспонирование матрицы: ![]() .
.
Свойство транспонирования произведения матриц: ![]() .
.
Невырожденная (неособая) матрица: ![]() .
.
Обратная матрица для невырожденной матрицы A: ![]() .
.
Свойства обратной матрицы:
1) ![]() ;
;
2) ![]() .
.
Виды матриц:
единичная матрица: 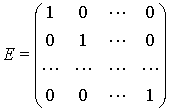
симметрическая матрица: ![]()
![]()
ортогональная матрица: A - невырождена и ![]()
кососимметрическая матрица: ![]() ;
;
матрица-строка: ![]()
матрица-столбец: ![]() .
.
Ранг матрицы ![]() - наибольший порядок её ненулевого минора или наибольшее число линейно независимых строк (столбцов) матрицы.
- наибольший порядок её ненулевого минора или наибольшее число линейно независимых строк (столбцов) матрицы.
1.3. Системы линейных уравнений
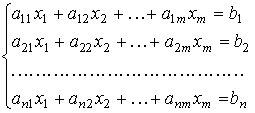 |
|
Матричный вид: ![]() ,
, ![]() - матрица системы,
- матрица системы,
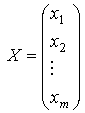 |
- столбец неизвестных, |
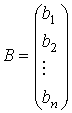 |
- столбец свободных членов. |
Совместность системы: ![]() , где
, где ![]() - расширенная матрица системы (теорема Кронекера-Капелли).
- расширенная матрица системы (теорема Кронекера-Капелли).
Формулы Крамера (n=m): ![]() ,
, ![]() - определитель матрицы системы;
- определитель матрицы системы; ![]() -определитель, полученный при замене i-го столбца матрица A на столбец В.
-определитель, полученный при замене i-го столбца матрица A на столбец В.
Однородная система (B=0):
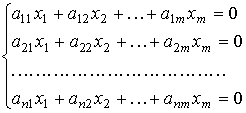 |
Если то система им то существуют ненулевые решения. |

