Пусть сигналы S1(t) = A cos w0t и S2(t) = 0 (дискретная амплитудная модуляция - ДАМ).

Подставим S2 = 0 в неравенство (4.4). Получим

_ _ _ _ _ _ _ _ _ _ _ _ _

[x(t) - S1(t)]2 < [x(t) - 0]2 , то S1 .

Преобразуем это выражение

_ _ _ _ _ _ _ _ _ _ _ _ _ _ _

x2(t) - 2x(t)S1(t) + S21(t) < х2(t) , то S1.

_ _ _ _ _ _ _ _ _ _ _

Сокращая на x2(t), получим x(t)S1(t) > S21(t)/2 , то S1 или, окончательно, BxS1(0) > РS1/ 2 , то S1 . (5.1)

Это - оптимальное правило решения приемника для известных сигналов с пассивной паузой. BxS1(0) - функция взаимной корреляции сигнала на входе приемника x(t) и ожидаемого сигнала S1(t), а РS1 - мощность сигнала S1(t) на входе приемника.

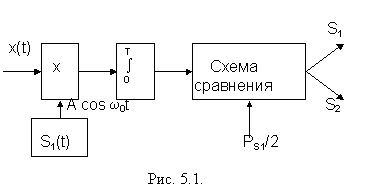
В соответствии с правилом (5.1) структурная схема приемника примет вид (рис. 5.1). В отличие от схемы (рис. 4.1) здесь вместо вычитания производится перемножение входного сигнала x(t) на опорное напряжение местного генератора сигналов S1(t) (в данном случае S1(t) = A cos w0t). Приведенная схема называется корреляционным приемником, так как вычисляется функция взаимной корреляции входного сигнала x(t) и местного сигнала S1(t), а в схеме сравнения функция корреляции сравнивается с некоторым порогом x0, значение которого равно 0,5РS1 ( когда P(S1) не равно P(S2), то в соответствии с неравенством (4.5) значение порога становится равным 0,5РS1 +s2n lnl0 ).

Правило решения (5.1) имеет простой физический смысл. Если функция взаимной корреляции сигнала x(t) и сигнала S1(t) достаточно велика, значит x(t) кроме помехи содержит также сигнал S1(t) и приемник выдает сигнал S1(t). Если же эта функция взаимной корреляции достаточно мала, значит x(t) не содержит сигнала S1(t), т.е. x(t) содержит только одну помеху. В этом случае приемник выдает сигнал S2(t).

Недостатком рассмотренной схемы является то, что для ее работы требуется знание мощности сигнала S1(t) на входе приемника. Однако очень часто эта мощность не является постоянной из-за замираний, изменения остаточного затухания в линиях связи и пр. Устройство для измерения мощности сигнала S1(t) на входе приемника становится сложным и недостаточно точным, что затрудняет практическую реализацию оптимального правила решения.