На Рис. 1.4 изображены ВАХ нелинейного элемента, график входного сигнала:

u(t)=U₀+U_mcosω₀t, (1.8)

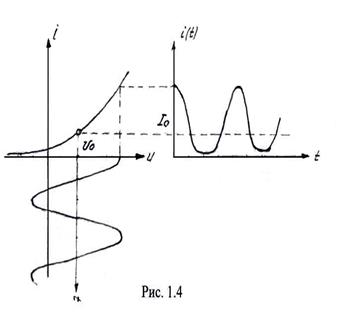и график выходного сигнала (тока, протекающего через НЭ). Форма тока существенно отличается от формы напряжения приложенного к нему. Воспользуемся степенной аппроксимацией ВАХ, ограничившись слагаемым третьей степени. Подставляя (1.8) в (1.6) и используя тригонометрические соотношения:

,

.

получим выражение для тока, протекающего через нелинейный элемент:

i(t)=I₀+I₁cosω₀t+I₂cos2ω₀t+ I₃cos3ω₀t+…, (1.9)

где ; ; ; (1.10)

Ток, протекающий через НЭ, содержит постоянную составляющую и совокупность гармоник, количество которых определяется наибольшей степенью аппроксимирующего полинома. При этом амплитуды четных гармоник определяются четными коэффициентами аппроксимирующего полинома, а нечетных гармоник – нечетными коэффициентами.

Анализ преобразования суммы двух гармонических сигналов при степенной аппроксимации ВАХ полиномом второй степени:

i=a₀+a₁(u-U₀)+a₂(u-U₀)². (1.11)

Входным сигналом в этом случае является колебание:

u(t)=U₀+U_m1cosω₁t+U_m2cosω₂t. (1.12)

Подстановка (1.12) в (1.11) и использование ранее приведенных тригонометрических соотношений и соотношения:

,

дает выражение для тока, протекающего через НЭ:

i(t)=I₀+I₁₁cosω₁t+I₁₂cosω₂t+I₂₁cos2ω₁t+I₂₂cos2ω₂t+

I_pcos(ω₁ – ω₂)t+ I_ccos(ω₁ + ω₂)t, (1.13)

где: ]; ; ; ; ; ;

. (1.14)

В этом случае ток, протекающий через НЭ содержит постоянную составляющую , гармоники кратных частот ω₁ , ω₂ , 2ω_{1 ,} 2ω₂ с амплитудами соответственно , , , и гармоники комбинационных частот: разностной частоты ω_p= ω₁ – ω₂ с амплитудой и суммарной частоты ω_с= ω₁ + ω₂ с амплитудой