Все широкополосные системы модуляции обеспечивают высокую помехоустойчивость при условии, что отношение сигнала к помехе qвх на входе приемника больше некоторого предельного (порогового) значения q![]() . При qвх<q
. При qвх<q![]() широкополосные системы теряют свои, преимущества (резко снижается помехоустойчивость) и связь становится практически невозможной. Рассмотренная в предыдущих главах теория помехоустойчивости справедлива для «малых» помех (qвх>q
широкополосные системы теряют свои, преимущества (резко снижается помехоустойчивость) и связь становится практически невозможной. Рассмотренная в предыдущих главах теория помехоустойчивости справедлива для «малых» помех (qвх>q![]() ). Значение порога практически определяет предельную дальность связи при заданной мощности передатчика. Поэтому важно определить это значение и установить закон изменения отношения сигнала к помехе на выходе приемника за порогом (приqвх<q
). Значение порога практически определяет предельную дальность связи при заданной мощности передатчика. Поэтому важно определить это значение и установить закон изменения отношения сигнала к помехе на выходе приемника за порогом (приqвх<q![]() )
)
Рассмотрим один из возможных методов решения этой задачи [2]. При передаче реальных сигналов емкость канала Ср и количество воспроизводимой на выходе приемника информации ![]() за время Т можно определить по формулам:
за время Т можно определить по формулам:
![]() (9.31)
(9.31)
![]() (9.32)
(9.32)
где δ и δт — коэффициенты, зависящие от статистических свойств сигнала и помехи. В реальной системе связи ![]() обычно меньше Ср. С уменьшением отношения сигнала к помехе qвх на входе приемника Ср и
обычно меньше Ср. С уменьшением отношения сигнала к помехе qвх на входе приемника Ср и ![]() уменьшаются. При этом оказывается, что емкость канала Ср уменьшается быстрее, чем количество принятой информации
уменьшаются. При этом оказывается, что емкость канала Ср уменьшается быстрее, чем количество принятой информации ![]() . При некотором значении q достигается равенство Ср=
. При некотором значении q достигается равенство Ср=![]() Поскольку
Поскольку ![]() не может быть больше Ср, то это равенство является предельным, определяющим пороговое значение сигнала к помехе qt. Дальнейшее уменьшение qвх ведет к резкому уменьшению qвых т. е. к увеличению ошибок (искажений) на выходе приемника. В этой области (qвх< qt) в лучшем случае может быть обеспечено лишь равенство Ср=
не может быть больше Ср, то это равенство является предельным, определяющим пороговое значение сигнала к помехе qt. Дальнейшее уменьшение qвх ведет к резкому уменьшению qвых т. е. к увеличению ошибок (искажений) на выходе приемника. В этой области (qвх< qt) в лучшем случае может быть обеспечено лишь равенство Ср=![]() , определяющее предельную помехоустойчивость приемника при большом уровне помех.
, определяющее предельную помехоустойчивость приемника при большом уровне помех.
Поясним теперь явление порога геометрически. Каждому сигналу s(t) соответствует точка в n-мерном пространстве, где n=2TF — база сигнала, а ансамблю возможных сигналов — некоторая область в этом пространстве (пространстве сигналов). При нормальном распределении область возможных сигналов будет представлять собой гиперсферу с радиусом ![]() , а область принятых сигналов x(t)=s(t)+ω(t) —сферу с радиусом
, а область принятых сигналов x(t)=s(t)+ω(t) —сферу с радиусом ![]() . Вокруг каждой точки переданного сигнала образуется область неопределенности, обусловленная помехой. Если помеха представляет собой белый шум, то эта область будет иметь сферическую форму с радиусом
. Вокруг каждой точки переданного сигнала образуется область неопределенности, обусловленная помехой. Если помеха представляет собой белый шум, то эта область будет иметь сферическую форму с радиусом ![]() . Максимальное число различимых точек сигнала М, очевидно, будет равно отношению объема сферы принятых сигналов Vx к объему шумовой сферы Vш. Объем n-мерной сферы, как известно, равен:
. Максимальное число различимых точек сигнала М, очевидно, будет равно отношению объема сферы принятых сигналов Vx к объему шумовой сферы Vш. Объем n-мерной сферы, как известно, равен:
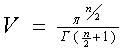
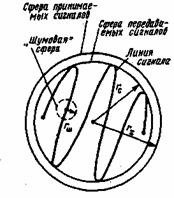
Рис. 9.1. К геометрической интерпретации порога
Тогда
![]()
Емкость канала определяется как logM, а пропускная способность
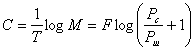
Так мы приходим к ранее полученной формуле Шеннона (6.87) для пропускной способности канала.
При передаче непрерывного сообщения u(t) передаваемый сигнал s(t, и) является функцией и. Следовательно, совокупности сообщений {u(i)}, лежащих в интервале (—1,+ 1), соответствует некоторая линия в пространстве сигнала. Форма и длина этой линии зависят от вида модуляции. Если максимальная мощность передаваемых сигналов ограничена, то линия сигналов будет расположена на поверхности или внутри псевдосферы радиуса rс =![]() . В двухмерном пространстве это будет линия, лежащая в круге радиуса rс (рис.9.1). Величина
. В двухмерном пространстве это будет линия, лежащая в круге радиуса rс (рис.9.1). Величина 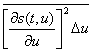 и характеризует длину отрезка, на который сместится изображающая точка по линии сигнала, когда передаваемое сообщение получит приращение
и характеризует длину отрезка, на который сместится изображающая точка по линии сигнала, когда передаваемое сообщение получит приращение ![]() . Очевидно, чем больше это смещение, тем меньше вероятность, что под действием помехи такое смещение произойдет.
. Очевидно, чем больше это смещение, тем меньше вероятность, что под действием помехи такое смещение произойдет.
Действительно, согласно (9.19) чем больше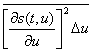 ,тем меньше будет ошибка из-за наложения помех. Таким образом, для увеличения помехоустойчивости следует выбирать такие системы передачи, для которых линия сигналов при изменении сообщения и от —1 до +1 будет наиболее длинной.
,тем меньше будет ошибка из-за наложения помех. Таким образом, для увеличения помехоустойчивости следует выбирать такие системы передачи, для которых линия сигналов при изменении сообщения и от —1 до +1 будет наиболее длинной.
Форма линии сигналов в общем cлучае отличается от формы .линии сообщений. Для системы ОБП линии сигналов и сообщений идентичны, а для систем с линейной модуляцией (AM, БМ ) — подобны. В случае широкополосных систем (например, ЧМ) линия сигналов имеет сложную извилистую форму (рис. 9.1). Длина линии увеличивается с увеличением полосы частот (индекса модуляции) сигнала. При ограниченной мощности сигнала (rc = const) удлинение линии ведет к сближению различных витков линии.
Число различимых точек сигнала, очевидно, равно числу непрерывающихся шумовых сфер на линии сигнала. Если уровень помех мал (соответственно мал радиус шумовых сфер), то число различимых точек будет сравнительно большим. Однако шумовые сферы вдоль линии сигнала будут занимать лишь небольшую часть объема сферы сигнала. Емкость канала в этом случае используется не полностью (Jp<Cp). За счет избыточной емкости ![]() С = СР—Jр обеспечивается значительный выигрыш системы
С = СР—Jр обеспечивается значительный выигрыш системы ![]() (9.30).
(9.30).
С увеличением уровня помех радиус шумовых сфер увеличивается, улучшается использование емкости канала, но одновременно уменьшается число различимых точек на линии сигнала (уменьшается помехоустойчивость). При некотором уровне помех шумовые сферы соседних витков сигнала будут касаться друг друга. В этом предельном случае объем сферы сигнала будет плотно заполнен шумовыми сферами. Это означает, что вся емкость канала используется для передачи информации (JР=СР). При дальнейшем увеличении уровня помех шумовые сферы будут перекрываться, а это может привести к тому, что по принятому сигналу будет воспроизведено сообщение, соответствующее точке сигнала, лежащей на соседнем витке. Появляются так называемые аномальные ошибки, резко снижающие помехоустойчивость системы связи. Таким образом, равенство JР=СР является предельным, определяющим порог помехоустойчивости.
Приравнивая Jр к Ср согласно (9.31) и (9.32) получим выражение для отношения сигнала к помехе на выходе приемника за «порогом» (qвх< qt)
![]() (9.33)
(9.33)
Вблизи порога, когда 1<qвх< qt
![]()
Выражение, определяющее отношение сигнала к помехе на выходе приемника до «порога» (qвх> qt), известно из теория "малых" помех. Согласно (9.2) это выражение в общем виде можно записать
![]() (9.34)
(9.34)
где ![]() зависит от вида модуляции. Пороговые значения qt и qt = qtвых можно определить путем решения следующей система уравнений, составленных «а основе (9.38) и (9.34):
зависит от вида модуляции. Пороговые значения qt и qt = qtвых можно определить путем решения следующей система уравнений, составленных «а основе (9.38) и (9.34):
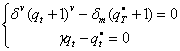 (9.35)
(9.35)
Практически эта система уравнений решается графически.
Рассмотрим отдельные виды модуляции на основании полу-чинных общих соотношений. Для однополосной системы (ОМ) v=l,![]() . Согласно (9.28) и (9.33) при qвх> qвых ,qвх = qвых при qвх < qt. Следовательно, порог в системе ОМ отсутствует.
. Согласно (9.28) и (9.33) при qвх> qвых ,qвх = qвых при qвх < qt. Следовательно, порог в системе ОМ отсутствует.
Для амплитудной модуляции v = 2. Полагая ![]() , из (9.23) имеем
, из (9.23) имеем
![]() (9.36)
(9.36)
а согласно (9.23)
![]() (9.37)
(9.37)
Решение системы ур-ний (9.35) с учетом экспериментальных данных для ![]() и
и ![]() дает значение
дает значение ![]() порядка единицы.
порядка единицы.
Таким образом, при условий, что полоса пропускания высокочастотной части приемника равна ширине спектра сигнал. При более широкой полосе пропускания ![]() возрастает и наблюдается быстрое уменьшение
возрастает и наблюдается быстрое уменьшение ![]() . ниже порога.
. ниже порога.
Для ЧМ v![]() 2m:
2m:
![]() (9.38)
(9.38)
![]() (9.39)
(9.39)
Решение системы ур-ний (9.35) для ЧМ сводится к решению алгебраического уравнения степени 2т. При ![]() и
и ![]() справедлива приближенная формула
справедлива приближенная формула
![]() (9.40)
(9.40)
В общем случае для любой системы модуляции можно считать
![]() (9.41)
(9.41)
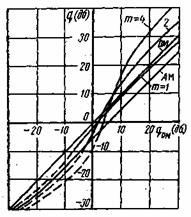
Рис. 9.2. Зависимость отношения сигнала к помехе на выходе приемника ЧМ (т=1,2,4), ОМ и AM от отношения сигнал/помеха на входе приемка ОМ
На рис. 9.2 приведена зависимость отношения сигнала к помехе на выходе приемника ЧМ ![]() при различных индексах модуляции. По оси абсцисс отложено отношение сигнала к помехе в децибелах на входе приемника ОМ, а по оси ординат — отношение сигнала к помехе в децибелах на выходе приемника ЧМ. Так как для ЧМ F
при различных индексах модуляции. По оси абсцисс отложено отношение сигнала к помехе в децибелах на входе приемника ОМ, а по оси ординат — отношение сигнала к помехе в децибелах на выходе приемника ЧМ. Так как для ЧМ F![]() 2mFm, а для ОМ F=Fm, то значение q на входе приемника определится как
2mFm, а для ОМ F=Fm, то значение q на входе приемника определится как
![]()
Кривые рассчитаны по ф-лам (9.38) и (9.39) с учетом экспериментальных данных для ![]() и
и ![]() . Для сравнения на этом же рисунке нанесены соответствующие кривые для AM и ОМ. Поскольку определение
. Для сравнения на этом же рисунке нанесены соответствующие кривые для AM и ОМ. Поскольку определение ![]() и
и ![]() при
при ![]() затруднительно, то кривые в этой области (пунктир) проведены ориентировочно.
затруднительно, то кривые в этой области (пунктир) проведены ориентировочно.
Из рисунка видно, что с увеличением индекса модуляции пороговое значение ![]() увеличивается и порог становится более резко выраженным. За порогом помехоустойчивость ЧМ сильно уменьшается и при сравнительно большом уровне помех становится хуже, чем помехоустойчивость систем ОМ и AM. При
увеличивается и порог становится более резко выраженным. За порогом помехоустойчивость ЧМ сильно уменьшается и при сравнительно большом уровне помех становится хуже, чем помехоустойчивость систем ОМ и AM. При ![]() порог выражен слабо и кривые для ЧМ приближаются к кривым для AM.
порог выражен слабо и кривые для ЧМ приближаются к кривым для AM.
Графическое решение системы ур-ний (9.35) для частотной модуляции при различных значениях v=2т показывает, что пороговое значение отношения сигнала к помехе на входе приемника qt при изменении индекса модуляции изменяется в пределах от 1 до 2. Пороговая мощность при этом изменяется в весьма широких пределах, поскольку
![]() (9.42)
(9.42)
где ![]() — мощность шума на входе приемника, пропорциональная ширине полосы пропускания приемника F и, следовательно, индексу модуляции m.
— мощность шума на входе приемника, пропорциональная ширине полосы пропускания приемника F и, следовательно, индексу модуляции m.
При малом уровне помех (![]() ) минимально необходимая мощность сигнала на входе приемника ЧМ при заданном
) минимально необходимая мощность сигнала на входе приемника ЧМ при заданном ![]() равна:
равна:
![]() (9.43)
(9.43)
С увеличением т эта мощность уменьшается. Здесь выигрыш γ, определяемый ф-лой (9.30), полностью реализуется.
При большом уровне помех (![]() ) величина выигрыша резко уменьшается и минимальная мощность сигнала практически определяется величиной порога
) величина выигрыша резко уменьшается и минимальная мощность сигнала практически определяется величиной порога ![]() . Увеличение индекса модуляция при этом может оказаться нецелесообразным. Из условия
. Увеличение индекса модуляция при этом может оказаться нецелесообразным. Из условия ![]() можно определить максимально допустимый индекс модуляции, при котором еще реализуется выигрыш γ и мощность сигнала определяется ф-лой (9.43). На основании (9.42) и (9.43) имеем
можно определить максимально допустимый индекс модуляции, при котором еще реализуется выигрыш γ и мощность сигнала определяется ф-лой (9.43). На основании (9.42) и (9.43) имеем
![]()
откуда
![]() (9.44)
(9.44)
Таким образом, оптимальный индекс модуляции тем выше, чем более высокие требования предъявляются к качеству передачи сообщений (величине ![]() ). При индексе модуляции, определяемом выражением (9.44), заданное значение
). При индексе модуляции, определяемом выражением (9.44), заданное значение ![]() достигается пря минимальной затрате мощности сигнала на входе. Однако в этих условиях малейшее уменьшение мощности входного сигнала приводит к переходу за порог, т. е. к резкому уменьшению
достигается пря минимальной затрате мощности сигнала на входе. Однако в этих условиях малейшее уменьшение мощности входного сигнала приводит к переходу за порог, т. е. к резкому уменьшению ![]() .
.
Полученные значения порога для различных видов модуляции (![]() ) являются предельными и в реальных приемниках могу» быть достигнуты, но не могут быть превзойдены. По экспериментальным данным порог в системе ЧМ при обычном способе приема наступает примерно при равенстве пиковых значений сигнала и помехи, что соответствует
) являются предельными и в реальных приемниках могу» быть достигнуты, но не могут быть превзойдены. По экспериментальным данным порог в системе ЧМ при обычном способе приема наступает примерно при равенстве пиковых значений сигнала и помехи, что соответствует ![]() . Это означает, что при большом уровне помех реальная помехоустойчивость приемника ЧМ значительно меньше потенциальной. Следовательно, имеется возможность путем усовершенствования схемы приемника снизить порог помехоустойчивости и тем самым увеличить дальность связи при той же мощности передатчика. Эта проблема стала особенно актуальной в связи с разработкой сверхдальних космических линий связи.
. Это означает, что при большом уровне помех реальная помехоустойчивость приемника ЧМ значительно меньше потенциальной. Следовательно, имеется возможность путем усовершенствования схемы приемника снизить порог помехоустойчивости и тем самым увеличить дальность связи при той же мощности передатчика. Эта проблема стала особенно актуальной в связи с разработкой сверхдальних космических линий связи.
Большинство методов снижения порога при ЧМ основано на принципе «сжатия» спектра сигнала в приемнике. Частотно-модулированный сигнал можно представить в виде синусоиды, положение которой на шкале частот меняется в соответствии с законом модуляции. Ширина полосы пропускания обычного ЧМ приемника выбирается такой, чтобы вмещать полезный сигнал в любой момент времени за период модуляции. Эта полоса намного превышает полосу частот передаваемого сообщения. Однако ЧМ сигнал не занимает эту полосу все время, можно лишь утверждать, что в любой момент времени он находится в некотором отрезке полосы. Наличие априорной информации о скорости изменения частоты сигнала позволяет осуществить слежение за этой частотой узкополосным приемником, что достигается введением обратной связи по частоте или применением следящего фильтра промежуточной частоты.
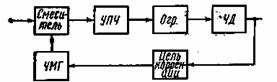
Рис. 9.3. Структурная схема приемника ЧМ сигналов с обратной связью по частоте
Структурная схема приемника с отрицательной обратной связью по частоте приведена на рис. 9.3. Обратная связь выбирается таким образом, чтобы синхронно с изменением частоты принимаемого сигнала в том же направлении изменялась частота гетеродина Г. Если обозначить коэффициент передачи прямого тракта через К, а коэффициент передачи цели обратной связи через β, то параметры ЧМ сигнала на выходе УПЧ (![]() и т') можно выразить через параметры входного сигнала (
и т') можно выразить через параметры входного сигнала (![]() и т) следующим образом.
и т) следующим образом.
![]() (9.45)
(9.45)
Как видим, девиация частоты ![]() в УПЧ оказывается меньше, чем на входе приемника. Поэтому полосу пропускания УПЧ можно сузить и тем самым уменьшить мощность шумов иа входе детектора, что согласно (9.42) влечет за собой снижение пороговой мощности сигнала.
в УПЧ оказывается меньше, чем на входе приемника. Поэтому полосу пропускания УПЧ можно сузить и тем самым уменьшить мощность шумов иа входе детектора, что согласно (9.42) влечет за собой снижение пороговой мощности сигнала.
Если полоса частот на входе смесителя равна F![]() 2Fm(1+m), то на выходе его при наличии обратной связи по частоте полоса
2Fm(1+m), то на выходе его при наличии обратной связи по частоте полоса
![]() (9.46)
(9.46)
При достаточно глубокой обратной связи можно получить ![]() . Спектр сигнала, таким образом снижается в m+1 раз. Следовательно, в пределе полоса пропускания тракта промежуточной частоты приемника может быть сужена в m+1 раз и во столько же раз снижен порог помехоустойчивости. Практически это предельное снижение порога не достигается. Эксперименты показывают, что таким образом можно снизить порог на 5—9 дб. Аналогичные результаты получаются в схеме со следящим фильтром (рис. 9.4).
. Спектр сигнала, таким образом снижается в m+1 раз. Следовательно, в пределе полоса пропускания тракта промежуточной частоты приемника может быть сужена в m+1 раз и во столько же раз снижен порог помехоустойчивости. Практически это предельное снижение порога не достигается. Эксперименты показывают, что таким образом можно снизить порог на 5—9 дб. Аналогичные результаты получаются в схеме со следящим фильтром (рис. 9.4).
Приемник со следящим фильтром отличается от приемника с обратной связью тем, что элементом, перестраиваемым под действием низкочастотного выходного сигнал, является узкополосный фильтр в тракте промежуточной частоты.
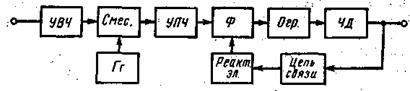
Рис. 9.4. Структурная схема приемника ЧМ со следящим фильтром.
При этом входной тракт, УПЧ, ограничитель и ЧД выполняются широкополосными, как и в обычном ЧМ приемнике. Следящий фильтр представляет собой узкополосный LC-контур, перестраиваемый по частоте в пределах полосы, равной удвоенной девиации частоты сигнала. Основные соотношения, описывающие процесс снижения порога, здесь получаются примерно такими же, как и для приемника с обратной связью. Минимальная полоса частот узкополосного фильтра не должна быть меньше удвоенной высшей модулирующей частоты Fm.
В описанных схемах снижения порога сжатие спектра сигнала и соответствующее сужение полосы пропускания тракта УПЧ приемника в равной степени уменьшают как сигнал, так и помеху, поэтому отношение сигнала к помехе на выходе приемника при работе до порога не изменяется.
Схемы снижения порога, приведенные в данном параграфе, являются разновидностями схем квазиоптимального приемника (рис. 5.12 и 5.13). Во всех этих схемах слежение осуществляется за мгновенной частотой сигнала.

