Всестороннее исследование характеристик ОВ может быть проведено только на основе волновой теории, путём решения уравнений Максвелла, которые для продольных составляющих электрического Е_z и магнитного Н_z полей применительно к сердцевине двухслойного ОВ, ось которого совмещена с осью z цилиндрической системы координат, имеют вид [7]

,

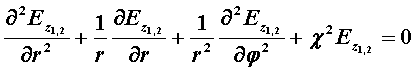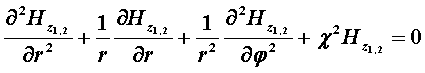, (3.2.1)

где

c – поперечный коэффициент распространения волны в сердцевине волокна;

b – продольный коэффициент распространения;

n – коэффициент преломления.

k₀ – волновое число;

e₀ и m₀ – диэлектрическая и магнитная проницаемость среды соответственно, а индексы 1 и 2 соответствуют параметрам сердцевины и оболочки. Поскольку волокно выполняется из немагнитного материала, то m₀ = 1, следовательно

.

Как известно, в силу отличия физических процессов распространения волн в сердцевине и оболочке ОВ для решения данных систем уравнений используются различные функции. Так, для сердцевины решения ищутся в виде функций Бесселя и записываются как [7]

Решения уравнений для оболочки выражаются через функцию Ганкеля и имеют вид

.

Поперечные составляющие векторов сердцевины и оболочки выражаются через комбинацию продольных составляющих Е_z и Н_z и при r£R представляются в виде

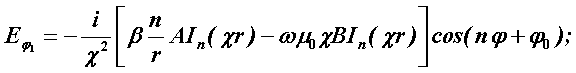
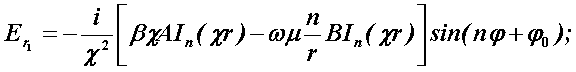
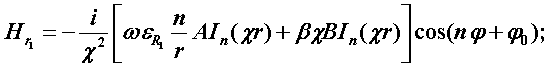
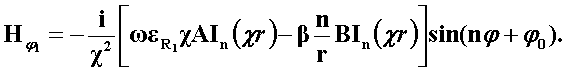
Соответственно при r ³ R имеем:

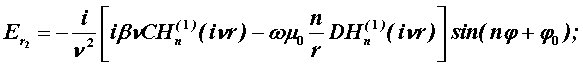
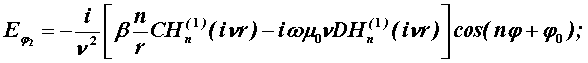
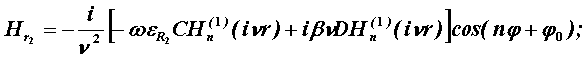
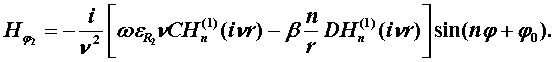
Постоянные интегрирования A, B, C, D в последних выражениях определяются из граничных условий на поверхности раздела сред при r = R, которые задаются как

; ;

; .

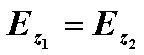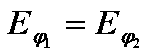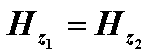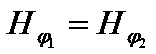В результате имеет место следующая однородная система уравнений:

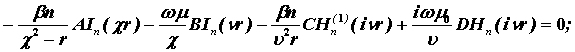
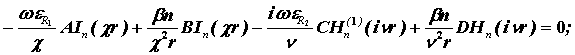
Приравнивая к нулю определитель полученной системы уравнений, решение ищется относительно b в виде так называемого основного дисперсионного уравнения [7]:

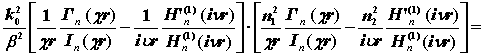
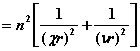. (3.2.2)

Данное уравнение позволяет найти решение относительно b и рассчитать структуру поля в сердцевине и в оболочке оптического волокна, зная значения поперечных коэффициентов распространения c и n.

В общем случае уравнения такого вида имеют ряд решений, каждому из которых соответствует определённый тип волны, называемый модой, которая определяется сложностью структуры поля, в частности числом максимумов и минимумов в поперечном сечении, и обозначается двумя числовыми индексами n и m. Индекс n означает число изменений поля по периметру ОВ, а индекс m – число изменений поля по диаметру.

В оптическом волокне могут распространяться два типа волн: симметричные продольные Е_nm и Н_nm, у которых по одной продольной составляющей, и несимметричные волны, имеющие одновременно по две продольные составляющие, одна из которых ЕН_nm с преобладанием электрической составляющей Е_z и другая НЕ_nm с преобладанием магнитной составляющей Н_z. При m>0 имеем гибридные моды, а при m=0 – поперечные моды TE₀₁ и TH₀₁.

В случае симметричных мод, у которых поле не зависит от азимутального угла j, правая часть дисперсионного уравнения равна нулю, и оно распадается на два уравнения:

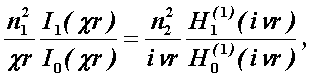
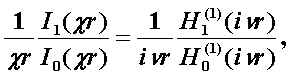(3.2.3)

первое из которых определяет характеристики составляющих направлений магнитных Н-мод, в которых Е_z=0, Н_z¹0, а второе – электрических Е-мод с Е_z¹0 и Н_z=0.

Очевидно, что изменение значений n₁, n₂, r и l приводит к изменению числа решений данных дисперсионных уравнений и, следовательно, числа распространяющихся в волокне симметричных мод.

Чем меньше диаметр d_c, тем меньше сечение светового потока, поступающего в оптическое волокно, тем меньше различных типов колебаний (обусловленных множеством решений уравнения Максвелла), или мод, возникает в оптоволокне. Волокно, в котором распространяется несколько мод, называется многомодовым (ММ), а то, в котором распространяется одна мода - одномодовым (ОМ). Для промышленно выпускаемых световодов ОМ-волокно имеет диаметр 7-10 мкм, а ММ-волокно - 50; 62,5; 85 и 100 мкм . В ОМ-волокне поддерживается только одна гибридная мода НЕ₁₁, называемая основной модой, в ММ-волокне поддерживаются различные, как поперечные, так и гибридные, моды.