4.5.1. Обнаружение сигналов в дифференциальной модуляции PSK

4.5.2. Пример бинарной модуляции DPSK

4.5.3. Некогерентное обнаружение сигналов FSK

4.5.4. Расстояние между тонами для некогерентной ортогональной передачи сигналов FSK

4.5.4.1. Минимальное расстояние между тонами и ширина полосы

4.5.4.2. Дуальные соотношения

4.5.1. Обнаружение сигналов в дифференциальной модуляции PSK

Название дифференциальная фазовая манипуляция (differential phase-shift keying — DPSK) иногда требует некоторого пояснения, поскольку со словом "дифференциальный" связано два различных аспекта процесса модуляции/демодуляции: процедура кодирования и процедура обнаружения. Термин "дифференциальное кодирование" употребляется тогда, когда кодировка двоичных символов определяется не их значением (т.е. нуль или единица), а тем, совпадает ли символ с предыдущим или отличается от него. Термин "дифференциальное когерентное обнаружение" сигналов в дифференциальной модуляции PSK (именно в этом значении обычно используется название DPSK) связан со схемой обнаружения, которая зачастую относится к некогерентным схемам, поскольку не требует согласования по фазе с принятой несущей. Стоит отметить, что дифференциально кодированные сигналы PSK иногда обнаруживаются когерентно. Эта возможность будет рассмотрена в разделе 4.7.2.

В некогерентных системах не предпринимаются попытки определить действительное значение фазы поступающего сигнала. Следовательно, если переданный сигнал имеет вид

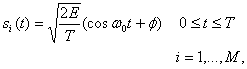
то принятый сигнал можно описать следующим образом.

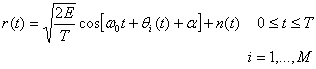(4.41)

Здесь α — произвольная константа, обычно предполагаемая случайной переменной, равномерно распределенной между нулем и 2π, a n(t) — процесс AWGN.

Для когерентного обнаружения используются согласованные фильтры (или их эквиваленты); для некогерентного обнаружения подобное невозможно, поскольку в этом случае выход согласованного фильтра будет зависеть от неизвестного угла а. Но если предположить, что а меняется медленно относительно интервала в два периода (2T), то разность фаз между двумя последовательными сигналами и не будет зависеть от α.

(4.42)

Основа дифференциального когерентного обнаружения сигналов в дифференциальной модуляции PSK (DPSK) состоит в следующем. В процессе демодуляции в качестве опорной фазы может применяться фаза несущей предыдущего интервала передачи символа. Ее использование требует дифференциального кодирования последовательности сообщений в передатчике, поскольку информация кодируется разностью фаз между двумя последовательными импульсами. Для передачи i-го сообщения (i= 1, 2,.... М) фаза текущего сигнала должна быть смещена на радиан относительно фазы предыдущего сигнала. Вообще, детектор вычисляет координаты поступающего сигнала путем определения его корреляции с локально генерируемыми сигналами и . Затем, как показано на рис. 4.16, детектор измеряет угол

между вектором текущего принятого сигнала и вектором предыдущего сигнала.

Вообще, схема DPSK менее эффективна, чем PSK, поскольку в первом случае, вследствие корреляции между сигналами, ошибки имеют тенденцию к распространению (на соседние времена передачи символов). Стоит помнить, что схемы PSK и DPSK отличаются тем, что в первом случае сравнивается принятый сигнал с идеальным опорным, а во втором — два зашумленных сигнала. Отметим, что модуляция DPSK дает вдвое больший шум, чем модуляция PSK. Следовательно, при использовании DPSK следует ожидать вдвое (на 3 дБ) большей вероятности ошибки, чем в случае PSK; ухудшение качества передачи происходит довольно быстро с уменьшением отношения сигнал/шум (вопрос достоверности передачи при использовании модуляции DPSK рассмотрен в разделе 4.7.5). Преимуществом схемы DPSK можно назвать меньшую сложность системы.

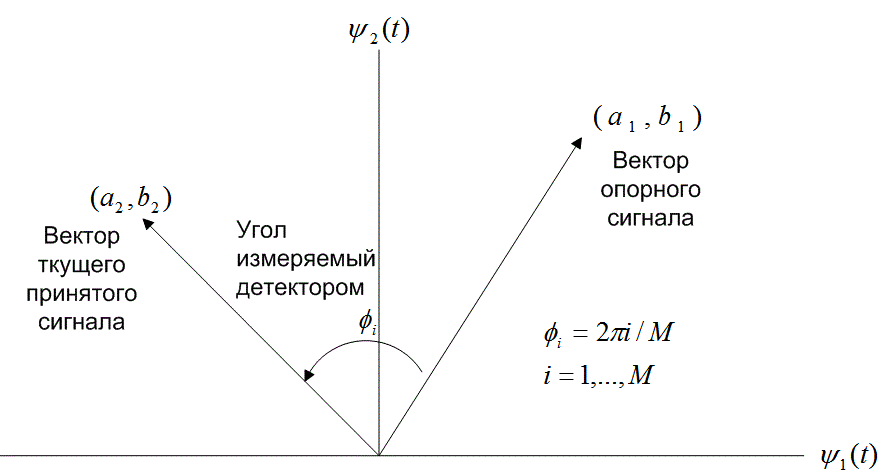
Рис. 4.16. Сигнальное пространство для схемы DPSK

4.5.2. Пример бинарной модуляции DPSK

Суть дифференциального когерентного обнаружения в схеме DPSK состоит в том, что информация из сигнала извлекается путем изменения фазы от символа к символу. Следовательно, переданный сигнал требуется вначале закодировать. На рис. 4.17, а представлено дифференциальное кодирование двоичного потока сообщений , где k — индекс дискретизации. Дифференциальное кодирование начинается (третья стро­ка на рисунке) с произвольного выбора первого бита кодовой последовательности c(k = 0) (в данном случае выбрана единица). Затем последовательность закодирован­ных битов c(k) может, в общем случае, кодироваться одним из двух способов.

(4.43)

или

(4.44)

Здесь символ "" представляет сложение по модулю 2 (определенное в разделе 2.9.3), а черта над выражением означает его дополнение. На рис. 4.17, а дифференциальное кодирование сообщения было выполнено с помощью уравнения (4.44). Другими сло­вами, текущий бит кода с(k) равен единице, если бит сообщения m(k) совпадает с пре­дыдущим закодированным битом c(k- 1), в противном случае — c(k)=0. В четвертой строке рисунка кодированная последовательность битов c(k) преобразовывается в по­следовательность сдвигов фаз , где единица представляется сдвигом фазы на 180°, а нуль — нулевым сдвигом фазы.

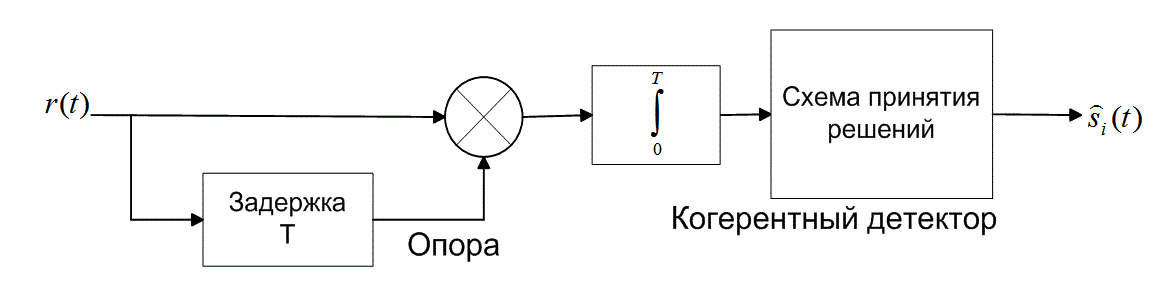
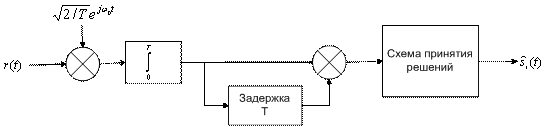
На рис. 4.17, б в виде блочной диаграммы представлена схема обнаружения бинарных сигналов в модуляции DPSK. Отметим, что основным элементом демодуля­тора на рис. 4.7 является интегратор произведений; как и при когерентном обнару­жении сигналов PSK, мы пытаемся определить корреляцию принятого сигнала с опорным. (Опорный сигнал — это просто запаздывающая версия принятого сигна­ла.) Другими словами, в течение каждого интервала передачи символа мы согласо­вываем принятый символ с предыдущим на предмет корреляции или антикорреля­ции (отличия в фазе на 180°).

а)

Обнаруженное сообщение, 1 1 0 1 0 1 1 0 0 1

б)

в)

Рис. 4.17. Дифференциальная фазовая манипуляция (DPSK): а) дифференциальное кодирование; б) дифференциальное когерентное обнаружение; в) оптимальное дифференциальное когерентное обнаружение

Пусть при отсутствии шума принятый сигнал с последовательностью сдвигов фаз поступает в коррелятор, изображенный на рис. 4.17, б. Фаза совпадает с ; обе имеют одинаковое значение, π. Следовательно, первый бит обнаружен­ного выхода — . Далее совпадает с , и снова имеем то же значение . Затем отличается от , так что , и т.д.

Необходимо отметить, что детектор, изображенный на рис. 4.17, б, является близ­ким к оптимальному [3] в смысле вероятности ошибки. Оптимальный дифференци­альный детектор для схемы DPSK требует согласования опорной несущей с принятой несущей по частоте, но не обязательно по фазе. Отсюда — вид оптимального диффе­ренциального детектора, приведенного на рис. 4.17, в [4]. Достоверность передачи при использовании такого детектора рассмотрена в разделе 4.7.5. Обратите внимание на то, что опорный сигнал (рис. 4.17, в) приведен в комплексной форме записи ; это показывает необходимость квадратурной реализации, использующей квадратурный и синфазный компоненты (см. раздел 4.6.1).

4.5.3. Некогерентное обнаружение сигналов FSK

Детектор, выполняющий некогерентное обнаружение сигналов в модуляции FSK, описываемых уравнением (4.8), можно реализовать с помощью корреляторов, подобных показанным на рис. 4.7. При этом оборудование приема следует настроить как детектор энергии без измерения фазы. По этой причине некогерентный детектор обычно требует вдвое большего числа ветвей-каналов, чем когерентный. На рис. 4.18 показаны синфазный (I) и квадратурный (Q) каналы, используемые для некогерентного обнаружения набора сигналов в бинарной модуляции FSK (BFSK). Отметим, что две верхние ветви настроены на обнаружение сигнала с частотой для синфазной ветви опорный сигнал имеет вид , а для квадратурной — . Подобным образом две нижние ветви настроены на обнаружение сигнала с частотой ; для синфазной ветви опорный сигнал имеет вид , а для квадратурной — . Предположим, что принятый сигнал r(t) имеет вид точно , т.е. фаза точно равна нулю. Следовательно, сигнальный компонент принятого сигнала точно соответствует (по частоте и фазе) опорному сигналу верхней ветви. В такой ситуации максимальный выход должен дать интегратор произведений верхней ветви. Вторая ветвь должна дать нулевой выход (проинтегрированный шум с нулевым средним), поскольку ее опорный сигнал ортогонален сигнальному компоненту сигнала r(t). При ортогональной передаче сигналов (см. раздел 4.5.4) третья и четвертая ветви также должны дать выходы порядка нуля, поскольку их опорные сигналы также ортогональны сигнальному компоненту сигнала r(t).

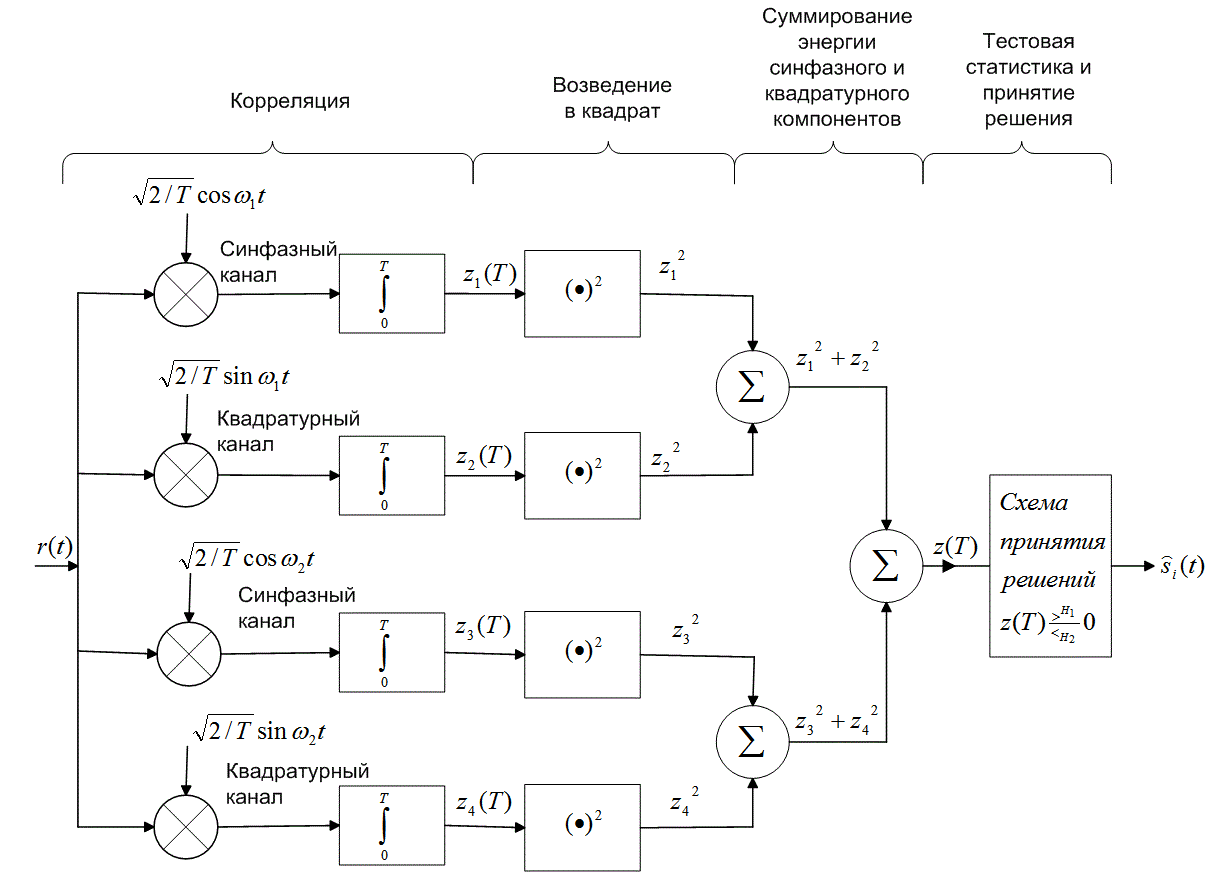
Рис. 4.18. Квадратурный приемник

Рассмотрим теперь другую возможность. Пусть принятый сигнал r(t) имеет вид . В этом случае максимальный выход должна дать вторая ветвь схемы (рис. 4.18), а выходы других ветвей должны быть порядка нуля. В реальной системе сигнал r(t) скорее всего описывается выражением , т.е. входящий сигнал будет частично коррелировать с опорным сигналом и частично — с сигналом . Поэтому некогерентный квадратурный приемник ортогональных сигналов и требует синфазной и квадратурной ветви для каждого возможного сигнала набора. Блоки, показанные на рис. 4.18 после интеграторов произведений, выполняют операцию возведения в квадрат, что предотвращает появление возможных отрицательных значений. Затем для каждого класса сигналов набора (в бинарном случае — для двух) складываются величины из синфазного канала и из квадратурного канала. На конечном этапе формируется тестовая статистика z(T) и выбирается сигнал с частотой , или , в зависимости от того, какая пара детекторов энергии дала максимальный выход.

Существует еще одна возможная реализация некогерентного обнаружения сигналов FSK. В этом случае используются полосовые фильтры, центрированные на частоте с полосой , за которыми, как показано на рис. 4.19, следуют детекторы огибающей (envelope detector). Детектор огибающей состоит из выпрямителя и фильтра нижних частот. Детекторы согласовываются с огибающими сигнала, а не с самими сигналами. При определении огибающей фаза несущей не имеет значения. При бинарной FSK решение относительно значения переданного символа принимается путем определения, какой из двух детекторов огибающей дает большую амплитуду на момент измерения. Подобным образом для системы, использующей многочастотную фазовую манипуляцию (multiple frequency shift-keying — MFSK), решение относительно принадлежности переданного символа к одному из М возможных принимается путем определения, какой из М детекторов огибающей дает максимальный выход.

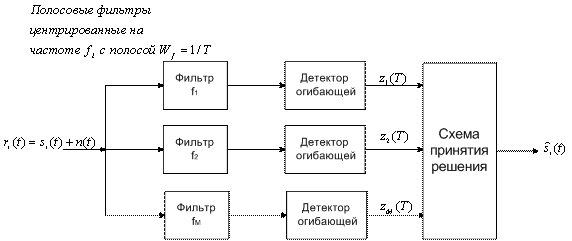
Рис. 4.19. Некогерентное обнаружение сигналов FSK с использованием детекторов огибающей

Детектор огибающей, изображенный на блочной диаграмме рис. 4.19, кажется проще квадратурного приемника, показанного на рис. 4.18, но не стоит забывать, что использование (аналоговых) фильтров обычно приводит к большей массе и стоимости детекторов огибающей по сравнению с квадратурным приемником. Поскольку квадратурные приемники могут реализовываться цифровым образом, с появлением больших интегральных схем их использование в качестве некогерентных детекторов стало предпочтительнее. Детектор, показанный на рис. 4.19, может реализовываться цифровым образом, использование аналоговых фильтров заменяется выполнением дискретного преобразования Фурье. Подобная структура обычно сложнее цифровой реализации квадратурного приемника.

4.5.4. Расстояние между тонами для некогерентной ортогональной передачи сигналов FSK

Частотная манипуляция (frequency shift keying — FSK) обычно реализуется как ортогональная передача сигналов, хотя ортогональными являются не все схемы FSK. Что мы подразумеваем под ортогональностью, когда речь идет о тонах сигнального множества? Предположим, что мы используем два тона f1= 10000 Гц и f2 = 11000 Гц. Ортогональны ли они между собой? Другими словами, удовлетворяют ли они критерию ортогональности (уравнение (3.39)) и не коррелируют ли в течение периода передачи символа T? Пока у нас недостаточно информации, чтобы ответить на этот вопрос. Вообще, тоны f1, и f2 являются ортогональными, если при переданном тоне f1 дискретная огибающая на выходе принимающего фильтра, согласованного с f2, дает нуль (т.е. отсутствуют перекрестные помехи). Подобная ортогональность между тонами сигнального множества FSK обеспечивается, если любая пара тонов множества разделена по частоте расстоянием, кратным 1/Г Гц. (Это доказывается ниже, в примере 4.3.) Тон с частотой f1, который включается на время передачи символа (Т с) и после этого выключается (такой, как тон FSK, приведенный в выражении (4.8)), аналитически можно описать следующим образом.

где

Из табл. А.1 находим Фурье-образ .

Здесь функция sinс определена выражением (1.39). Спектры подобных соседствующих тонов — тона 1 с частотой f1, и тона 2 с частотойf2 — показаны на рис. 4.20.

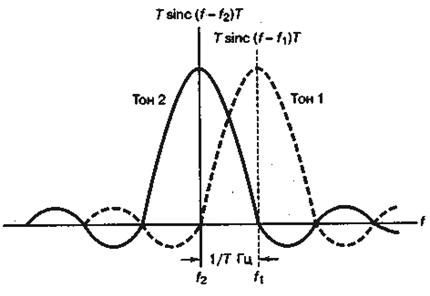
Рис. 4.20. Минимальное расстояние между тонами для ортогональной передачи сигналов FSK с некогерентным обнаружением

4.5.4.1. Минимальное расстояние между тонами и ширина полосы

Для того чтобы некогерентно обнаруживаемый тон давал максимальный сигнал на выходе "своего" фильтра и нулевой сигнал — на выходе любого соседнего фильтра (схема на рис. 4.19), максимум спектра тона 1 должен совпадать с одним из переходов через нуль спектра тона 2, а максимум спектра тона 2 должен приходиться на один из переходов через нуль спектра тона 1. Расстояние по частоте между центром спектрального главного лепестка и первым переходом через нуль является минимальным необходимым расстоянием между тонами. При некогерентном обнаружении это соответствует минимальному расстоянию между тонами, которое, как показано на рис. 4.20, равно 1/Т Гц. Несмотря на то что использование схемы FSK подразумевает передачу в течение каждого интервала передачи символа всего одного однополосного тона, когда мы говорим о ширине полосы сигнала, подразумеваем спектр, достаточный для всех тонов M-арного множества. Следовательно, для модуляции FSK требования к полосе связаны со спектральным расстоянием между тонами. Можно считать, что с каждым из группы соседствующих тонов связан спектр, простирающийся в обе стороны от максимального значения на величину, равную половине расстояния между тонами. Следовательно, для бинарной модуляции FSK, изображенной на рис. 4.20, ширина полосы передачи равна спектру, находящемуся между тонами, плюс области слева и справа, ширина которых равна половине расстояния между тонами. Общий спектр, таким образом, равен удвоенному расстоянию между тонами. Экстраполируя этот результат на M-арный случай, получаем, что ширина полосы сигнала в ортогональной модуляции MFSK с некогерентным обнаружением равна M/T.

До сих пор мы рассматривали только некогерентное обнаружение сигналов в ортогональной модуляции FSK. Будет ли отличаться критерий минимального расстояния между тонами (и, как следствие, ширина полосы) при когерентном обнаружении? Разумеется, да. Как будет показано ниже, в примере 4.3, при использовании когерентного обнаружения минимальное расстояние между тонами снижается до 1/2T.

4.5.4.2. Дуальные соотношения

Инженерную концепцию дуальности можно определить следующим образом. Два процесса (функции, элемента или системы) дуальны друг другу, если описывающие их математические соотношения идентичны, с точностью до фигурирующих в них переменных (например, время и частота). Рассмотрим передачу сигналов FSK, где, как показано на рис. 4.20, модулированные сигналы имеют вид функций sinc (fT). Данная длительность тона определяет минимальное расстояние по частоте между тонами, необходимое для получения ортогональности. Это соотношение в частотной области имеет дуальное ему во временной области — передачу импульсов (рис. 3.16, б), где прямоугольным участкам полосы соответствуют импульсы вида sine (tIT). Данная ширина полосы определяет минимальное расстояние (на временной оси) между импульсами, необходимое для получения нулевой межсимвольной интерференции.

Пример 4.3. Минимальное расстояние между тонами для ортогональной FSK

Рассмотрим два сигнала и , используемые для некогерентной передачи сигналов FSK, где . Скорость передачи символов равна 1/Т символов/с, где Т — длительность символа, а φ — произвольный постоянный угол между 0 и 2π.

а) Докажите, что минимальное расстояние между тонами для ортогональной передачи сигналов FSK с некогерентным обнаружением равно 1/Т.

б) Чему равно минимальное расстояние между тонами для ортогональной передачи сигналов FSK с когерентным обнаружением?

Решение

а) Чтобы два сигнала были ортогональными, они должны удовлетворять условию ортогональности, которое дается выражением (3.69).

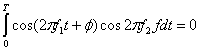(4.45)

Используя основные тригонометрические соотношения, приведенные в формулах (Г.6)и(ГЛ)-(Г.З), можно переписать выражение (4.4S) в виде

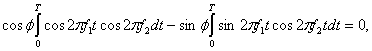(4.46)

так что

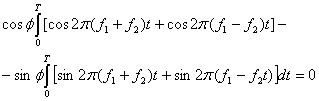(4.47)

что дает

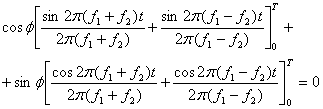(4.48)

или

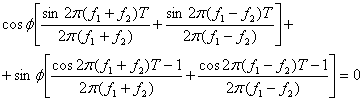(4.49)

Далее можно предположить, что ; это позволяет записать следующее.

(4.50)

Затем, объединяя выражения (4.49) и (4.50), можем записать следующее.

(4.51)

Отметим, что при произвольной фазе φ выражение (4.51) всегда справедливо, только если и при этом .

Поскольку

и

,

где п и k — целые, условия sin х = 0 и cos x = 1 удовлетворяются одновременно при п = 2k, Следовательно, из формулы (4.51) для произвольного φ можем записать следующее.

или (4.52)

Минимальное расстояние между тонами для ортогональной передачи сигналов FSK с некогерентным обнаружением получаем при к = 1, при этом

(4.53)

Напомним вопрос, сформулированный выше. Имея два тона f1 = 10 000 Гц и f2 = 11 000 Гц, мы спрашивали, являются ли они ортогональными? Теперь у нас достаточно информации для ответа на поставленный вопрос. Ответ связан со скоростью передачи сигналов FSK. Если манипуляция сигналами (переключение сигналов) происходит со скоростью 1 000 символов/с и используется некогерентное обнаружение, то сигналы ортогональны. Если манипуляция происходит быстрее, скажем со скоростью 10 000 символов/с, сигналы не ортогональны.

б) При некогерентном обнаружении, рассмотренном в п. а, расстояние между тонами, превращающее сигналы в ортогональные, было найдено посредством выполнения уравнения (4.45) для любой произвольной фазы. В случае когерентного обнаружения расстояние между тонами находится, если положить φ = 0. Причина в том, что мы знаем фазу принятого сигнала (ее дает контур ФАПЧ). Этот принятый сигнал будет коррелировать с каждым опорным сигналом, причем в качестве фазы опорного сигнала используется фаза принятого сигнала. Уравнение (4.51) можно теперь переписать с учетом φ = 0.

(4.54)

или

(4.55)

Минимальное расстояние между тонами для ортогональной передачи сигналов FSK с когерентным обнаружением получаем при k=l, при этом

(4.56)

Следовательно, при одинаковых скоростях передачи символов когерентное обнаружение требует меньшей ширины полосы, чем некогерентное, обеспечивая при этом ортогональную передачу сигналов. Можно сказать, что передача сигналов FSK с когерентным обнаружением более эффективно использует полосу. (Вопрос эффективности использования полосы подробно рассмотрен в главе 9.)

При когерентном обнаружении тоны расположены более плотно, чем при некогерентном, поскольку, если расположить два периодических сигнала так, чтобы их начальные фазы совпадали, ортогональность будет получена автоматически в силу симметрии (четности и нечетности) соответствующих сигналов в течение одного периода передачи символа. Это является отличием от способа получения ортогональности в п. а, где мы не уделяли внимания фазе. В случае когерентного обнаружения регулировка фазы в разрядах коррелятора означает, что мы можем расположить тоны ближе (по частоте) друг к другу, при этом по-прежнему поддерживая ортогональность в наборе тонов FSK. Вы можете доказать это самостоятельно, изобразив две синусоиды (или косинусоиды, или последовательности прямоугольных импульсов). Начальная фаза всех сигналов должна быть одинаковой (удобнее всего взять ее равной 0 радиан). Используя миллиметровку, выберите удобную временную шкалу для представления одного периода передачи символа Т. Изобразите тон с периодом Т, а затем изобразите другой тон, имеющий такую же начальную фазу, как и предыдущий, и период 2/3T. Выполните численное суммирование произведений тонов (смещенных относительно друг друга на 1/2T) и докажите, что они действительно являются ортогональными.