Включение RLC-контура на постоянное напряжение

Рассмотрим случай нулевых начальных условий u_C(0_–) = 0, i(0_–) = 0, когда RLC-контур включается на постоянное напряжение (рис. 6.14).

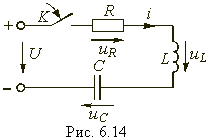
Отличие данного случая от рассмотренного выше заключается в нулевых начальных условиях и наличии принужденной составляю щей u_Cпр = U. Свободная составляющая u_Cсв определяется, как и ранее, уравнениями (6.43), (6.51) или (6.59) в зависимости от вида корней р₁ и р₂. Постоянные интегрирования А₁ и А₂ находятся при этом из начальных условий i(0_–) = 0, u_C(0_–) = 0 и законов коммутации для i и u_C. Определим, например, закон изменения u_C, i и u_L в случае, когда корни р₁ и р₂ — вещественные и различные. При этом u_{C св} определяются уравнением (6.43), а напряжение u_C и ток i имеют следующий вид: 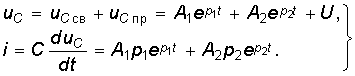(6.64)

Для нахождения коэффициентов А₁ и А₂ используем начальные условия u_C(0_– ) = 0 и i(0_– ) = 0, а также законы коммутации, определяемые выражениями (6.1),(6.2): (6.65)

Тогда (6.66)

Окончательные уравнения для и_С, i, и_L имеют вид 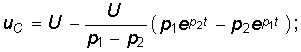(6.67) 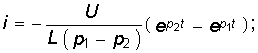(6.68) 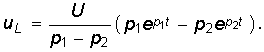(6.69)

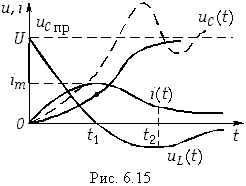
На рис. 6.15 изображены графики зависимостей (6.67)—(6.69), где моменты времени t₁ и t₂ определяются уравнениями (6.49). Сравнение формул (6.67)—(6.69) с (6.46)—(6.48) показывает, что ток i и напряжение и_L отличаются только знаком, а напряжение и_С — наличием постоянной составляющей U.

Аналогичным можно найти уравнения напряжений и тока для случая R < 2: 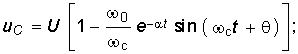(6.70) 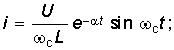(6.71) 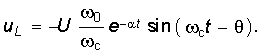(6.72)

На рис. 6.15 штриховой линией показана зависимость (6.70), которая свидетельствует о колебательном характере заряда емкости. Таким же образом можно получить уравнения для u_C, i и u_L для случая критического заряда емкости С при R = 2.

Включение RLC-контура на гармоническое напряжение

При включении RLC-контура на гармоническое напряжение u = U_msin(t + _u ) принужденная составляющая напряжения на емкости (6.73) где _C = _u + — /2. Здесь фазовый сдвиг между током в контуре и приложенным напряжением (6.74) а амплитуда принужденного напряжения на емкости 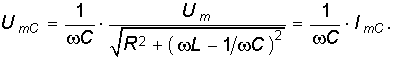(6.75)

Учитывая, что колебательный контур в радиотехнических устройствах, как правило имеет высокую добротность, т. е. выполняется условие R 2, то свободная составляющая u_Cсв определяется уравнением (6.51), и закон изменения напряжения на емкости будет иметь вид (6.76)

Взяв производную от выражения (6.76), и учтя, что для заданного контура , получим уравнение тока (6.77)

Постоянные интегрирования A и находим из начальных условий и законов коммутации: (6.78)

Откуда 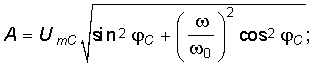(6.79) (6.80)

Подставив значения А и из уравнений (6.79), (6.80) в (6.76) и (6.77), получим окончательный закон изменения напряжения на емкости и тока в RLC-контуре: 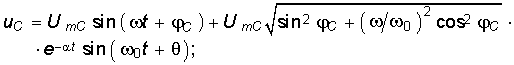(6.81) 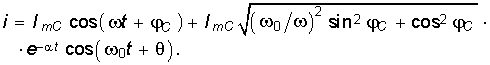(6.82)

Анализ уравнений (6.81), (6.82) показывает, что в случае, когда частота приложенного напряжения существенно превышает резонансную частоту контура ₀ при _C 0 в цепи могут возникнуть сверхнапряжения, а в случае и _C /2 — сверхтоки.

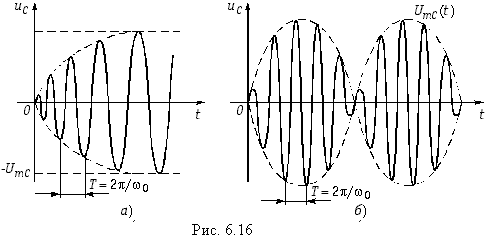
Если частота задающего напряжения = ₀, то при этом в цепи возникают явления изохронизма, когда напряжение на емкости и ток в контуре плавно изменяется в соответствии с уравнениями: (6.83) (6.84)

При этом переходный процесс протекает без перенапряжений и сверхтоков (рис. 6.16, а).

В случае, когда частота заданного напряжения и резонансная частота контура ₀ близки между собой, то в контуре возникают явления биений. Положим, что a = 0, тогда 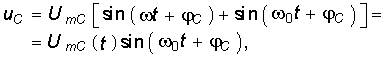(6.85) где U_mС(t) = 2U_mСсost — амплитуда биений с угловой частотой = ( — ₀ )/2. На рис. 6.16, б, показан график изменения напряжений биений (6.85).