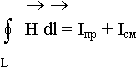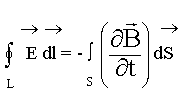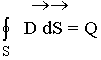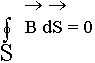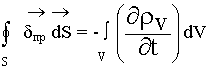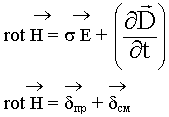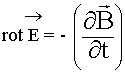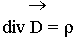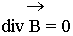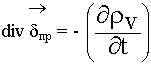3.1. Первое уравнение Максвелла
3.2. Второе уравнение Максвелла
3.3. Третье уравнение Максвелла
3.4. Четвертое уравнение Максвелла
Интегральные уравнения не позволяют получать информацию об электромагнитных процессах в каждой точке пространства. Они дают усредненные решения полей в пространстве.
Хорошо развитый аппарат математических решений позволят переходить от интегральной формы к дифференциальным решениям.
Впервые переход от интегральных уравнений к дифференциальным сделал Максвелл.
3.1. Первое уравнение Максвелла
Первое уравнение Максвелла является дифференциальной формулировкой закона полного тока:
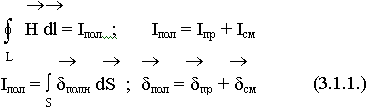
S - опирается на контур L.
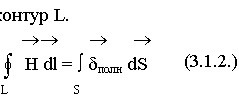
Используем теорему Стокса:
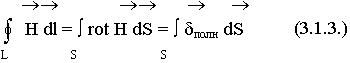
Равенство сохраняет силу по любой поверхности, опирающейся на контур L, отсюда следует, что подинтегральные функции равны.
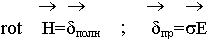- дифференциальная форма закона Ома.
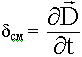
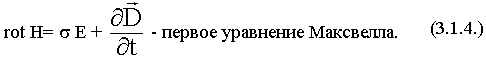
Физический смысл 1-го уравнения Максвелла.
Источниками вихревых магнитных полей являются токи проводимости и токи смещения.
3.2. Второе уравнение Максвелла
Второе уравнение Максвелла является дифференциальной формулировкой закона электромагнитной индукции:
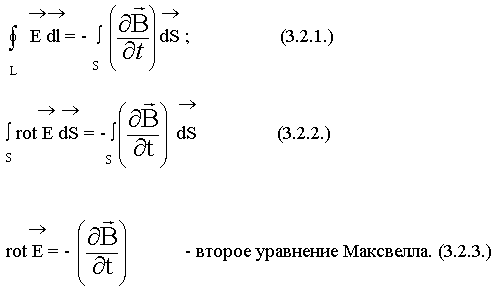
Физический смысл. Вихревое электрическое поле создается переменным магнитным полем.
3.3. Третье уравнение Максвелла
Третье уравнение Максвелла является дифференциальной формулировкой теоремы Гаусса для электрических полей.
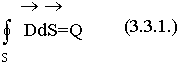
Воспользуемся теоремой Остроградского-Гаусса, которая позволяет осуществить переход от
поверхностного интеграла П (
) к объемному интегралу от (div D):
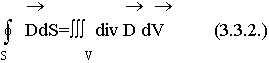
Запишем правую часть уравнения (3.3.1.) для объемного заряда. Объединим два выражения:
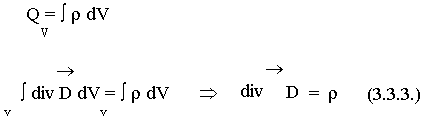
- третье уравнение Максвелла. (3.3.3.)
Физический смысл. Источниками электрического поля (векторов Е и D) являются заряды с плотностью r .
3.4. Четвертое уравнение Максвелла
Четвертое уравнение Максвелла является дифференциальной формулировкой теоремы Гаусса для магнитных полей:
Физический смысл. Дивергенция вектора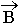 
любой точке пространства равняется нулю, т.е. - источников нет (магнитные заряды в природе отсутствуют). Нет ни стоков, ни источников.
3.5. Закон сохранения заряда в дифференциальной форме
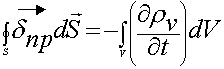
Используем теорему Остроградского-Гаусса:
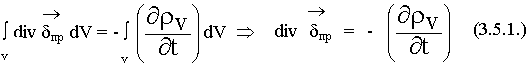
- это уравнение является следствием из предыдущих уравнений
3.6. Таблица интегральных и дифференциальных уравнений электромагнитного поля
Материальные уравнения среды.
= 
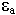
Все эти уравнения являются обобщением в математической форме опытов всего человечества об электромагнитных явлениях. Они не доказываются и не выводятся - это результат опытов.
= 
= 
= 
|
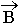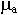
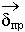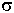
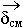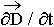
Интегральные уравнения электромагнитного поля |
Дифференциальные уравнения электромагнитного поля. Уравнения Максвелла |
|
1. Закон полного тока:
2. Закон электромагнитной индукции:
3. Теорема Гаусса для электрических полей:
4. Теорема Гаусса для магнитных полей:
5. Закон сохранения заряда
|
|
