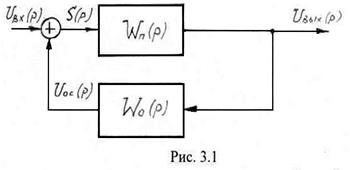
Радиотехнической цепью с обратной связью называется цепь у которой выходной сигнал вновь подается на вход цепи. На Рис. 3.1 представлена обобщенная структурная схема цепи с обратной связью (ЦОС). Из этого рисунка следует, что цепь с обратной связью является сложной, состоящей из цепи прямой связи и цепи обратной связи, через которую выходной сигнал возвращается на вход.

В практической радиотехнике обычно цепь прямой связи является активной (резонансный усилитель), а цепь обратной связи – пассивной цепью.

Для определения характеристик цепи с обратной связью воспользуемся операторным методом. Как известно, передаточная функция цепи:

. (3.1)

Но, как следует из Рис. 3.1:

, (3.2)

где – передаточная функция цепи прямой связи,

– сигнал рассогласования.

В свою очередь

, (3.3)

, (3.4)

где – сигнал обратной связи;

– передаточная функция цепи обратной связи.

Подстановка (3.4) в (3.3) и результата этой подстановки в (3.2) дает

.

Откуда в соответствии с (3.1) следует, что передаточная функция цепи с обратной связью

. (3.5)

Комплексный коэффициент передачи определяется из (3.5) заменой

. (3.6)

Так как

, (3.7)

, (3.8)

где , – амплитудно-частотные характеристики (АЧХ), , – фазо-частотные характеристики (ФЧХ), соответственно цепей прямой и обратной связи,

то подстановка (3.7) и (3.8) в (3.6) дает

. (3.9)

При , , входной сигнал и сигнал обратной связи складываются синфазно и модуль комплексного коэффициента передача ЦОС

, (3.10)

больше модуля комплексного коэффициента передачи цепи прямой связи. В этом случае обратная связь называется положительной.

Если же , , то входной сигнал обратной связи складываются в противофазе и обратная связь называется отрицательной. При этом

. (3.11)

Для оценки устойчивости цепей с обратной связью предложены различные критерии-правила, в соответствии с которыми можно судить устойчива цепь или нет.

Основной критерий устойчивости основан на решении характеристического уравнения

, (3.12)

где – коэффициенты линейного дифференциального уравнения, описывающего цепь

.

Согласно основному критерию устойчивости цепь является устойчивой, если действительные части всех корней характеристического уравнения (3.12) отрицательны.

Помимо основного критерия используются алгебраический критерий Гурвица и частные критерии Михайлова и Найквиста, подробно изложенные в рекомендованной литературе.

В заключение отметим, что при , цепь с положительной обратной связью становится неустойчивой, т.е. в ней возникают незатухающие колебания. Это явление лежит в основе построения автогенераторов колебаний различной формы.