9.1. Интеграл Фурье

9.2. Основные теоремы спектрального анализа

9.3. Распределение энергии в спектре непериодического сигнала

9.4. Спектры типовых сигналов

9.5. Частотный анализ линейных электрических цепей при непериодических воздействиях

9.6. Условия безыскаженной передачи сигналов через линейную цепь

9.7. Связь между временными и частотными характеристиками электрических цепей

9.8. Вопросы и задания для самопроверки

9.1. Интеграл Фурье

Для анализа переходных процессов при воздействии на цепь сигналов произвольной формы наряду с временным и операторным методом широко используется частотный метод анализа, базирующийся на спектральных представлениях сигнала.

Для непериодических сигналов используются спектральные представления, основанные на паре преобразований Фурье. Преобразование Фурье может быть получено предельным переходом от ряда Фурье (5.6). Для этого зададим непериодический сигнал f(t), удовлетворяющий условию абсолютной интегрируемости в бесконечных пределах (рис. 9.1): 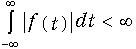. С физической точки зрения, это означает, что задается реализуемый сигнал с конечной энергией; при этом

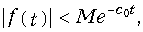
где М, с₀ — положительные постоянные величины.

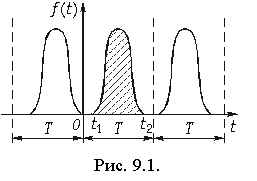
Условие (9.1) означает, что модуль |f(t)| имеет ограниченный показатель роста. Превратим мысленно этот сигнал в периодический повторением его через период Т (см. рис. 9.1). К полученному таким образом сигналу применимо разложение (5.6), которое после перехода к переменной t можно записать в виде

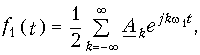
где

После подстановки А_k в уравнение (9.2) с учетом (9.3) получаем

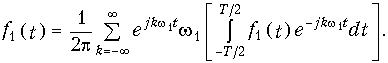
Переходя в уравнении (9.4) учитывая, что при этом w₁ dw и kw₁ w, а сумма вырождается в интеграл, получаем для исходного сигнала

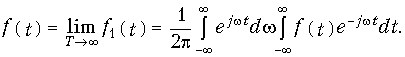
Внутренний интеграл в уравнении (9.5) носит название спектра сигнала F(jw):

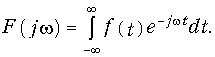
Тогда формула (9.5) принимает вид

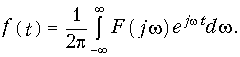
Уравнения (9.6) и (9.7) являются основными в теории спектрального анализа, причем (9.6) называется прямым, а (9.7) — обратным преобразованием Фурье. По аналогии с А_k спектр F(jw) является в общем случае комплексной функцией частоты и может быть записан в алгебраической форме

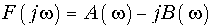
и показательной форме

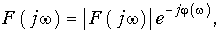
где

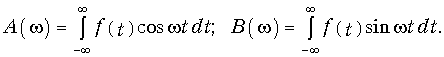
Модуль

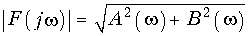
определяет амплитудный, а аргумент

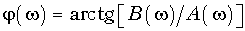
— фазовый спектр сигнала. Причем, как и для периодического сигнала, амплитудный спектр является четной, а фазовый — нечетной функцией частоты. Физический смысл преобразования Фурье лучше всего проявляется при представлении обратного преобразования (9.7) в тригонометрической форме. Если подставить вместо F(jw) в (9.7) его значение из (9.9), то получим

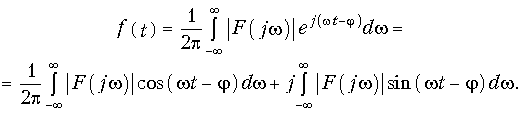
Учитывая, что |F(jw)| — четная, а синус — нечетная функция частоты интеграл от второго слагаемого равен нулю. Следовательно, принимая во внимание четность подынтегрального выражения в первом слагаемом, обратное преобразование Фурье имеет вид

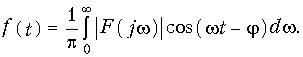
Из (9.13) следует важнейший вывод о том, что непериодический сигнал может быть представлен пределом суммы (интеграл) бесконечно большого числа бесконечно малых гармонических колебаний с амплитудами (1/p)|F(jw)| и начальными фазами j = j(w), причем, учитывая, что разность частот соседних гармоник бесконечно мала Dw = dw, то F(jw) в уравнении (9.13) представляет непрерывный сплошной спектр в отличии от спектра периодического сигнала, который является дискретным (линейчатым). Поэтому F(jw) называют комплексной спектральной плотностью, a |F(jw)| — спектральной плотностью амплитуд непериодического сигнала.

Смысл комплексного спектра F(jw) следует из связи между спектрами периодических и непериодических сигналов. Сравнение уравнений (9.3) с (9.6) позволяет установить эту связь между спектрами: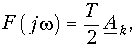

и спектр комплексных амплитуд A_k обращается в комплексную спектральную плотность F(jw).

Из (9.14) следует и другой важный вывод: модуль спектральной плотности непериодического сигнала и огибающая линейчатого спектра периодического сигнала, полученного повторением с периодом Т непериодического сигнала, совпадают по форме и отличаются только масштабом. Это наглядно можно проиллюстрировать на примере периодической последовательности прямоугольных импульсов (см. рис. 5.3, а): с увеличением периода (скважности q) спектр становится гуще (см. рис. 5.4, б) и в пределе при T = ¥ периодический сигнал превращается в непериодический (рис. 9.2), а дискретный спектр обращается в сплошной (рис. 9.3). При этом огибающая как линейчатого, так и сплошного спектра описывается функцией отсчетов (5.29): sinx/x.

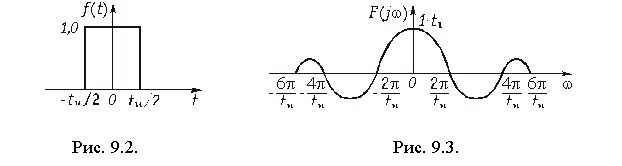
Рассмотрим некоторые основные свойства преобразования Фурье. Если сигнал f(t) является четной функцией времени, то, его спектр F(jw) — вещественный. Действительно, согласно (9.6) для F(jw) можно записать:

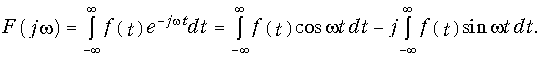
Второй интеграл равен нулю в силу нечетности подынтегральной функции, следовательно,

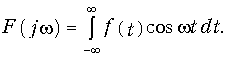
Аналогично при нечетности сигнала f(t) спектр F(jw) является чисто мнимым.

Важным свойством преобразования Фурье является взаимозаменяемость переменных t и w. Для четного сигнала f(t) и вещественного спектра F(jw) можем заменить в преобразовании (9.6) знаки перед jwt:

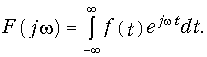
Тогда сравнивая (9.16) и (9.7) видим их подобие. Взаимозаменяемость переменных в преобразовании Фурье позволяет установить связь между частотными и временными характеристиками сигнала.

В соответствии с (9.8) и (9.9) сигнал может быть задан либо с помощью своего амплитудного |F(jw)| и фазового спектра j(w), либо с помощью вещественной A(w) и мнимой частей B(w) спектра сигнала. Причем, все они взаимосвязаны между собой согласно (9.11)—(9.12), т. е. нельзя задавать независимо амплитудный |F(jw)| и фазовый спектр j(w), или вещественную A(w) и мнимую часть спектра B(w).

Наиболее ясно эта связь проявляется для сигнала, заданного на положительной полуоси времени t:

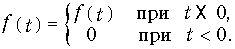
Перепишем (9.13) в форме

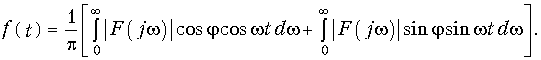
Или учитывая, что

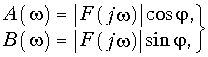
при t 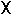0 получим:

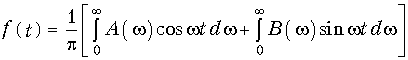
и при t < 0 с учетом (9.17)

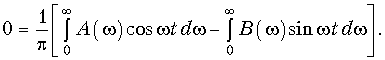
Суммируя и вычитая равенства (9.19) и (9.20), получаем:

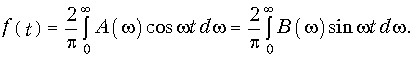
Отсюда следует связь между вещественной A(w) и мнимой B(w) частями спектра сигнала:

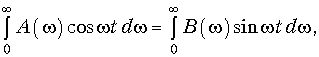
т. е. в данном случае сигнал f(t) полностью определяется только вещественной A(w) или мнимой B(w) частями комплексного спектра F(jw).

В заключение отметим, что при w = 0 спектр (9.6) принимает значение

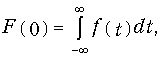
т. е. будет равен площади, ограниченной сигналом f(t). Формула (9.23) позволяет в ряде случаев оценить спектр сигнала по виду функции f(t).

Следует подчеркнуть, что временное и спектральное представление является просто двумя формами (моделями) представления реального физического процесса, и они лежат в основе временных и частотных методов анализа электрических цепей.

В заключение установим связь между преобразованием Фурье и преобразованием Лапласа. Если положить, что f(t) удовлетворяет условию (9.17), то прямое преобразование Фурье принимает вид

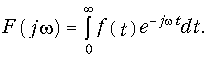
Соотношение (9.24) носит название одностороннего преобразования Фурье, так как оно определяется на положительной полуоси t. Если принять в качестве частного случая в формуле (7.1) a = 0, то р = jw, и прямое преобразование Лапласа (7.2)

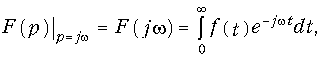
т. е. полностью совпадает с односторонним преобразованием Фурье (9.24).

Аналогично получим для обратного преобразования Лапласа (7.4) с учетом того, что dp = jdw:

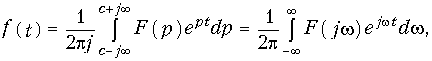
что полностью совпадает с (9.7).

Таким образом, преобразование Фурье есть частный случай преобразования Лапласа при a = 0. Следует подчеркнуть, что преобразование Фурье имеет более узкую область применения, чем преобразование Лапласа, так как условие (9.1), которым должны удовлетворять функции, преобразуемые по Фурье более жесткое, чем условие (7.3). Всякая функция, для которой применимо преобразование Фурье (9.6) всегда может быть преобразована по Лапласу, но не наоборот. В этой связи изображение F(p) можно трактовать как своего рода обобщенный спектр сигнала f(t).

9.2. Основные теоремы спектрального анализа

Как было установлено выше, между сигналом и его спектром существует однозначная связь, определяемая прямым преобразованием Фурье. Поскольку в процессе передачи сигнала он подвергается различным преобразованиям, очень важно установить как при этом изменяется спектр сигнала. Это имеет большое значение с точки зрения выбора оптимальных методов передачи, приема, требований к параметрам канала связи.

Рассмотрим основные теоремы о спектрах, имеющих практическое применение в электросвязи. Учитывая связь между преобразованием Фурье и Лапласа и имея в виду доказательства основных теорем, остановимся только на физической интерпретации основных теорем спектрального анализа.

Спектр суммы сигналов (теорема линейности) равен сумме спектров этих сигналов. Это свойство является следствием линейности преобразования Фурье. В более общем виде оно может быть записано следующим образом: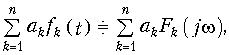

где a_k — коэффициенты разложения; 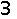— знак соответствия между сигналом и его спектром, определяемого парой преобразований Фурье.

Сдвиг сигнала во времени f(t—t₀) соответствует умножению его спектра на :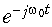

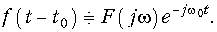
Из (9.28) следует важный вывод о том, что при сдвиге сигнала во времени его амплитудный спектр не изменяется, а фазовый изменяется пропорционально wt₀. Эта теорема имеет большое значение, так как в процессе обработки сигналов часто возникает необходимость осуществлять задержку сигнала.

Изменение масштаба независимого переменного (сжатие сигнала) описывается выражением

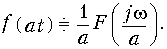
Из (9.29) следует, что сжатие сигнала во времени (а > 1) приводит к расширению спектра сигнала и напротив — растяжение сигнала (а < 1) — к сужению спектра.

Перемножение двух сигналов (теорема свертки). Спектр произведения двух функций f₁(t) и f₂(t) соответствует свертке их спектров F₁(jw) и F₂(jw):

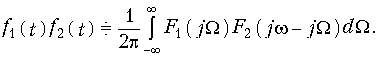
Важное значение имеет обратная теорема о произведении спектров сигналов:

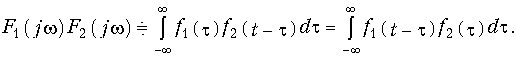
Свертка функций широко использовалась ранее во временных методах анализа электрических цепей.

Дифференцирование и интегрирование сигнала. При дифференцировании сигнала его спектр умножается на оператор jw:

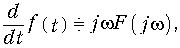
а при интегрировании делится на jw:

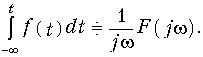
Доказательство (9.32)—(9.33) следует непосредственно из прямого и обратного преобразований Фурье. Следует подчеркнуть, что (9.33) справедливо для сигналов, удовлетворяющих условию F(0) = 0.

Смещение спектра сигнала на частоту 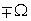соответствует умножению сигнала на оператор :

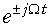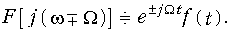
Теорема смещения (9.34) позволяет определить спектр модулированного сигнала и имеет большое значение в теории электрической связи.

9.3. Распределение энергии в спектре непериодического сигнала

Определим энергию сигнала f(t) по его спектральной характеристике F(jw). Предположим, что f(t) представляет собой напряжение или ток, протекающий в единичном сопротивлении R = 1 Ом. Тогда согласно (1.4) энергия выделяемая f(t) будет равна

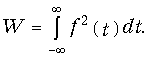
Представим подынтегральное выражение (9.35) в виде произведения 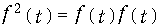и применим к f(t) обратное преобразование Фурье (9.7):

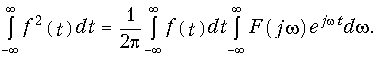
Учитывая независимость переменных t и w, перепишем последнюю формулу в виде

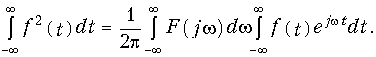
Внутренний интеграл представляет собой сопряженный спектр F(—jw). Если учесть, что 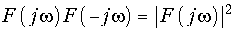, то получим следующее равенство Парсеваля (теорема Рэлея):

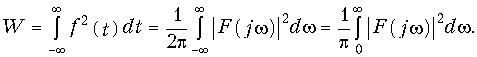
Из уравнения (9.36) следует, что величина |F(jw)|² представляет собой энергию сигнала, приходящуюся на 1 с^–1 текущей частоты w, поэтому квадрат модуля спектра |F(jw)|² называют спектральной плотностью энергии сигнала. Вид модуля |F(jw)| позволяет судить о распределении энергии в спектре непериодического сигнала. Равенство Парсеваля широко используется в теории цепей и сигналов при выборе полосы пропускания канала связи, обеспечивающей наилучшее использование энергии сигнала.

Следует отметить, что в отличие от формулы (5.23), где рассматривалась средняя за период Т мощность периодического несинусоидального сигнала, для непериодического сигнала такое усреднение невозможно ( 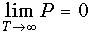). Общим для обеих случаев является то, что мощность и энергия сигналов не зависят от фаз спектральных составляющих.

9.4. Спектры типовых сигналов

Определим спектры наиболее распространенных типов электрических сигналов.

Единичная функция задается уравнением (7.19) (см. рис. 7.2, а). Строго говоря, функция (7.19) не удовлетворяет условию абсолютной интегрируемости, поэтому воспользуемся следующим приемом: умножим 1(t) на «гасящий» множитель е^–ct(с = const). При этом можно использовать прямое преобразование Фурье (9.6):

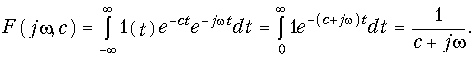
Преобразование F(jw, c) носит название обобщенного преобразования Фурье. Для получения спектра единичной функции перейдем к пределу:

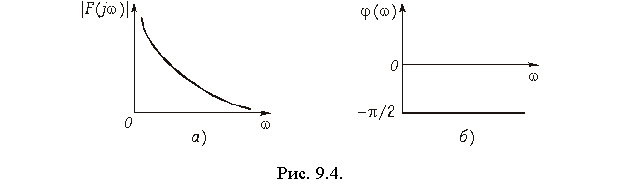
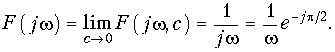
Из уравнения (9.38) получаем амплитудный |F(jw)| = 1/w (рис. 9.4, а) и фазовый спектр функции j(w) (рис. 9.4, б): j(w) = = —p/2, т. е. амплитудный спектр при w = 0 обращается в бесконечность, что свидетельствует о наличии в исходной функции 1(t) скачка при t = 0 (см. рис. 7.2, а). Для образования этого скачка в соответствии с (9.38) при t = 0 осуществляется суммирование бесконечно большого числа синусоидальных составляющих. Спектр (9.38) может быть получен и с помощью изображения единичной функции (7.20):

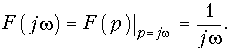
Единичная импульсная функция. Функция d(t) задается аналитически условиями (7.21). Для нахождения спектра d-функции воспользуемся прямым преобразованием Фурье (9.6), которое с учетом (9.8)—(9.10) можно записать в виде

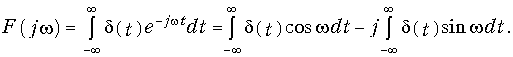
Так как второе слагаемое равно нулю, а первое — единице вследствие свойств (7.21)—(7.23), то окончательно получим

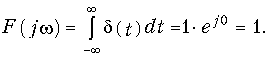
Таким образом, d-функция имеет равномерный амплитудный и нулевой фазовый спектры. Равенство нулю на всех частотах фазового спектра означает, что все гармонические составляющие d-функции, суммируясь с нулевыми начальными фазами, образуют при t = 0 пик бесконечно большого значения.

Следует отметить, что сдвиг d-функции на время t приводит согласно свойствам преобразования Фурье к спектру 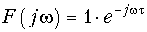, т. е. амплитудный спектр функции d(t—t) остается прежним, а фазовый изменяется пропорционально wt.

Из равенства (9.39) согласно обратному преобразованию Фурье (9.7) следует, что

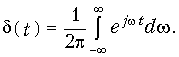
Учитывая условие взаимозаменяемости параметров t и w, последнее выражение можно переписать в следующем виде:

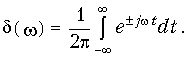
Уравнения (9.40) и (9.41) широко используются в теории сигналов и цепей.

Спектр постоянной составляющей функции a₀/2 = 1/2 с учетом (9.41) определяется уравнением

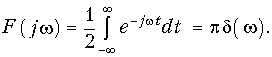
Таким образом, спектр постоянной составляющей равен нулю на всех частотах, кроме w = 0, где F(jw) обращается в бесконечность, то есть имеем на частоте w = 0 дискретную составляющую частоты в форме d-функции.

Спектр гармонического колебания. Проиллюстрируем методику использования прямого преобразования Фурье при определении спектра гармонического колебания

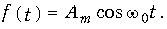
Преобразование (9.6) для функции (9.43) имеет вид

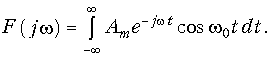
Формально функция (9.43) не удовлетворяет условию абсолютной интегрируемости, так как имеет показатель роста с = 0. По этому для вычисления интеграла (9.44) воспользуемся формулой Эйлера (3.18) и уравнением (9.41):

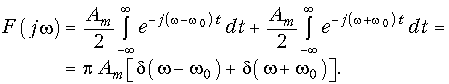
т. е. гармоническое колебание имеет дискретный спектр, состоящий из двух спектральных линий на частотах ±w₀.

Спектр одиночного прямоугольного импульса (см. рис. 9.2) можно найти как непосредственно из прямого преобразования Фурье (9.6), так и путем предельного перехода при q ® ¥ (T® ¥) в разложении (5.27). В результате получим

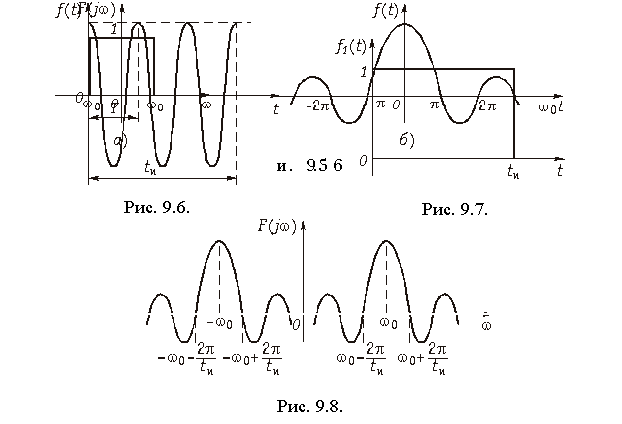
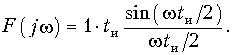
На рис. 9.3 изображен спектр одиночного импульса. Сравнение рис. 9.3 и рис. 9.4 показывает, что по своей форме спектр одиночного импульса совпадает с огибающей дискретного спектра последовательности периодических импульсов, однако спектр одиночного импульса является сплошным.

Из условия взаимосвязи между частотными и временными характеристиками сигнала следует, что сигнал с ограниченным по частоте ±w₀ спектром прямоугольной формы (рис. 9.5, а) имеет бесконечную протяженность и форму, аналогичную спектру прямоугольного импульса (рис. 9.5, б).

Спектр радиоимпульса (рис. 9.6) можно найти как произведение видеоимпульса прямоугольной формы (рис. 9.7) и гармонического колебания (9.43). Тогда, воспользовавшись теоремой свертки (9.30), получим:

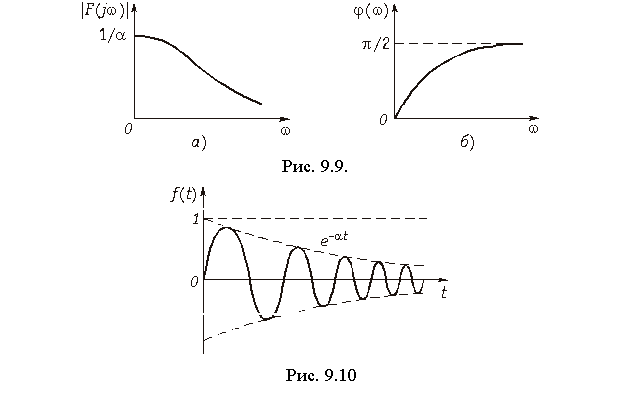
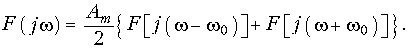
На рис. 9.8 показан вид спектра радиоимпульса.

Аналогичным образом можно найти спектр сигналов и более сложной формы.

Пример. Найти спектр экспоненциального импульса

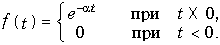
В соответствии с прямым преобразованием (9.6) получаем

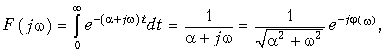
где 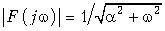— амплитудный (рис. 9.9, а) и 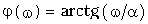—фазовый (рис. 9.9, б) спектры сигнала.

Пример 2. Определить спектр затухающего колебания (рис. 9.10)

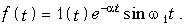
Согласно (9.6) находим

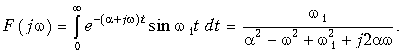
Отсюда находим спектры:

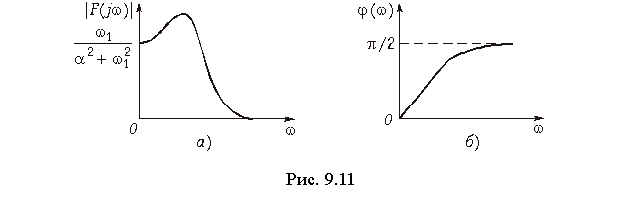
амплитудный (рис. 9.11, а)

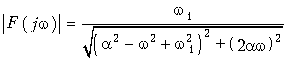
и фазовый (рис. 9.11, б)

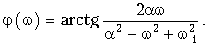
В таблице 9.1 приведены спектры некоторых наиболее распространенных сигналов.

9.5. Частотный анализ линейных электрических цепей при непериодических воздействиях

Представление непериодических сигналов в форме интеграла Фурье (9.6) и (9.7) позволяет применить к бесконечно малым гармоникам, составляющим его спектр. В частности, если цепь находится при нулевых начальных условиях (т. е. до начала входного воздействия в реактивных элементах цепи не была накоплена энергия электрического и магнитного полей), то по аналогии с (3.46), (3.48) и (3.49) можно записать законы Ома и Кирхгофа для спектров:

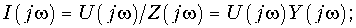
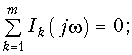
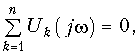
где I(jw), U(jw) — спектры токов и напряжений ветвей соответственно; ₁Z(jw) и Y(jw) имеют смысл комплексных сопротивлений и проводимостей ветвей. Законы Ома и Кирхгофа для спектров позволяют распространить рассмотренные ранее частотные методы анализа цепей при гармонических и периодических несинусоидальных воздействиях на непериодические сигналы.

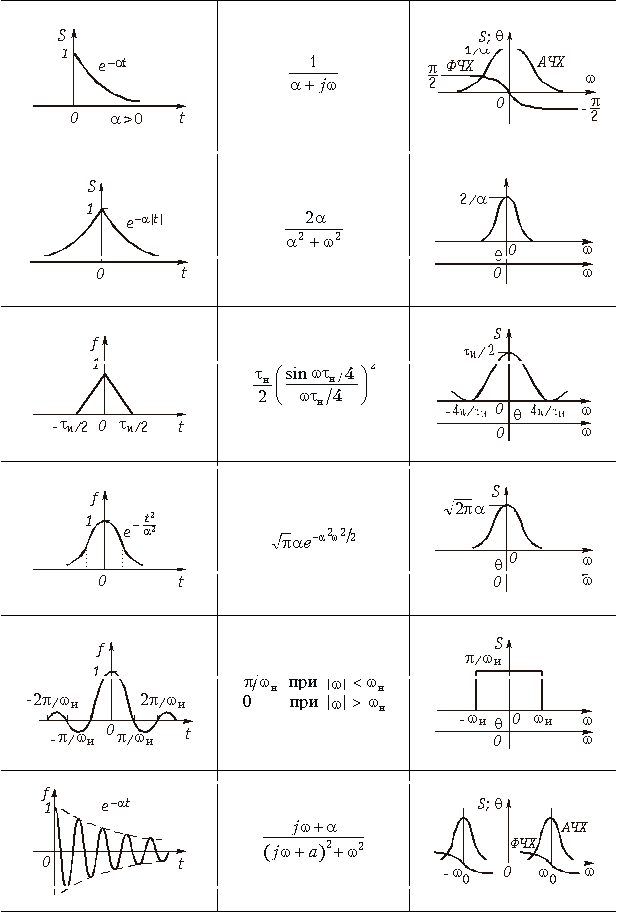
В случае, если необходимо найти выходную реакцию цепи в виде четырехполюсника при воздействии на входе непериодического сигнала, используют комплексную передаточную функцию цепи. При этом спектр выходной реакции согласно (4.1) и (4.2)

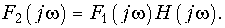
После определения спектра F₂(jw) выходная реакция f₂(t) может быть найдена с помощью обратного преобразования Фурье (9.7) или по таблицам.

Пример. Рассчитать спектральную плотность выходного сигнала в цепи (рис. 9.12), если на вход действует единичный импульс (рис. 9.7) с амплитудой U₁ = 4 В.

Для заданного входного сигнала (3.15) преобразование Фурье дает выражение

,

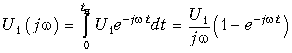которое после преобразований принимает более удобную форму (см. (9.46)):

.

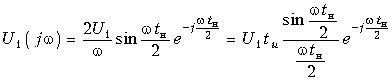Комплексная спектральная плотность выходного сигнала находится по формуле (9.51)

,

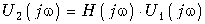где 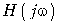– комплексная передаточная функция цепи по напряжению. Функция 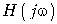находится как отношение комплексного значения гармонического напряжения 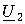на выходе цепи к комплексному значения гармонического напряжения 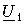той же частоты, приложенному ко входу цепи:

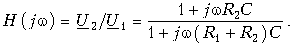
При этом спектральная плотность выходного сигнала:

.

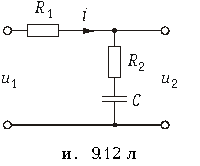
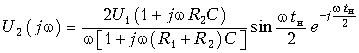Отсюда находим модули: спектральной плотности входного напряжения

;

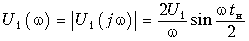АЧХ цепи

;

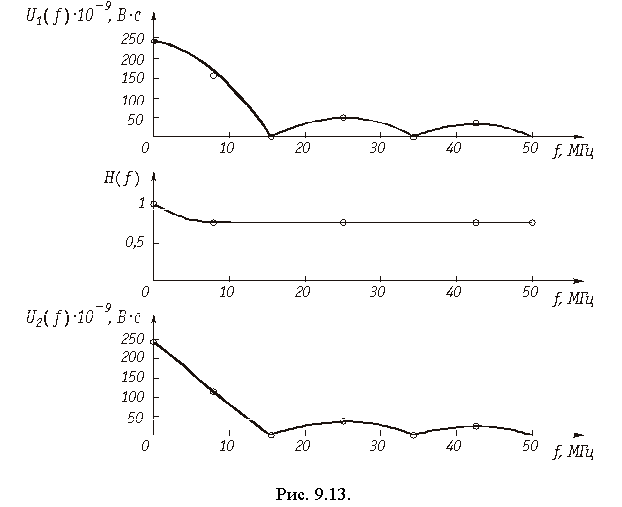
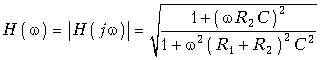спектральной плотности выходного напряжения

.

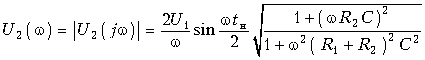На рис. 9.13 изображен спектр входного сигнала, АЧХ цепи и спектр выходного сигнала .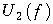

9.6. Условия безыскаженной передачи сигналов через линейную цепь

Частотный метод является достаточно эффективным и наглядным при анализе передачи сигналов через линейную систему. Он позволяет оценить частотные искажения в канале связи, требования к характеристикам электрической цепи. Особенно важно определить требования к АЧХ и ФЧХ цепи с точки зрения искажения формы сигнала. Определим условия неискажаемой передачи сигнала через линейную систему. Предположим, что на входе линейной цепи, как четырехполюсника действует сигнал f₁(t) определенной формы (рис. 9.12). На выходе в результате прохождения сигнала через четырехполюсник с комплексной передаточной функцией H(jw) амплитуда сигнала может измениться (на рис. 9.12 уменьшилась), и сигнал вследствие конечности скорости его распространения может запаздывать относительно входного воздействия на t₀. Однако важно, чтобы при этом не изменилась форма сигнала. Таким образом, условие безыскаженной передачи можно сформулировать с помощью равенства

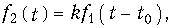
где k – некоторая вещественная постоянная; t₀ –время задержки (запаздывания) выходного сигнала относительно входного. Применив к (9.52) прямое преобразование Фурье и учтя свойство линейности и теорему запаздывания, перепишем условие (9.52) в частотной области:

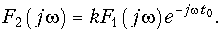
Так как комплексная передаточная функция цепи с учетом (4.5) должна быть

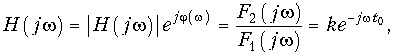
то отсюда получаем требование к АЧХ и ФЧХ неискажающей цепи

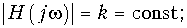
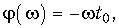
т. е. для того, чтобы линейная цепь не искажала форму сигнала ее АЧХ должна быть равномерной (рис. 9.13, а), а ФЧХ – линейной (рис. 9.13, б).

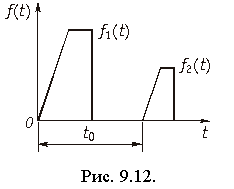
Условие безыскаженной передачи во всем частотном диапазоне можно выполнить лишь для резистивных цепей. В цепях с реактивными элементами условия (9.54) и (9.55) можно обеспечить лишь в ограниченном частотном диапазоне w₀ (на рис. 9.13 показано пунктиром).

В этой связи представляет практический интерес вопрос о влиянии на форму сигнала отклонения АЧХ и ФЧХ от идеальной. Рассмотрим в качестве примера прохождение сигнала в форме единичной функции, в форме единичного импульса и импульса прямоугольной формы через цепь с АЧХ, изображенной на рис. 9.14. Эта цепь соответствует идеальному ФНЧ и задается условием

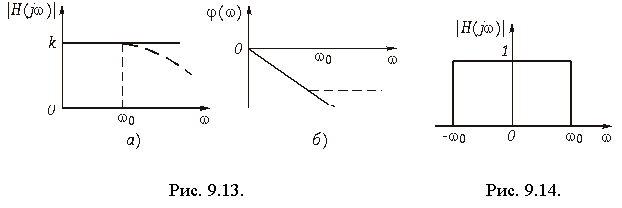
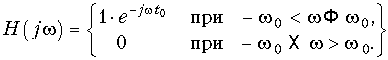
Фильтр нижних частот пропускает без искажений все частотные составляющие от 0 до w₀ и задерживает составляющие больше w₀.

Единичный импульс. Рассмотрим вначале входной сигнал f₁(t) в форме единичного импульса (рис. 7.2, б). Так как для единичного импульса F₁(jw) = 1, то с учетом (9.56) и обратного преобразования Фурье (9.7), получим:

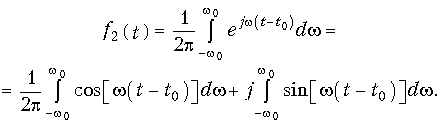
Учитывая, что второй интеграл равен нулю, окончательно после интегрирования получаем:

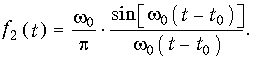
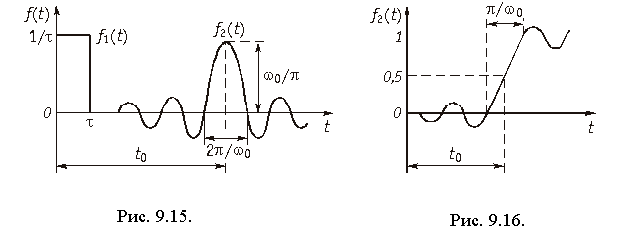
На рис. 9.15 изображена форма выходного сигнала f₂(t), определяемая функцией (9.57). Из рисунка видно, что форма выходного сигнала существенно отличается от входного импульса f₁(t): он искажается по форме и растягивается во времени (теоретически на бесконечность), что отражает установленное ранее соотношение между длительностью сигнала и шириной его спектра: сигнал ограниченный по частоте — бесконечен во времени и наоборот. Запаздывание выходного сигнала t₀ определяется крутизной ФЧХ: t₀ = —dj/dw). С увеличением w₀ (с расширением полосы пропускания фильтра) ширина главного лепестка импульса равная 2p/w₀ — сужается, задержка t₀ уменьшается, амплитуда импульса увеличивается. Важно отметить, что теоретически согласно (9.57) сигнал f₂(t) существует и при t < 0, т. е. до воздействия входного сигнала, что конечно, противоречит условию физической реализуемости и является следствием идеализации АЧХ ФНЧ.

Единичный сигнал. Рассмотрим теперь прохождение сигнала в форме единичной функции (рис. 7.2, а) через ФНЧ с характеристикой (9.56). Запишем уравнение единичной функции 1(t) в интегральной форме:

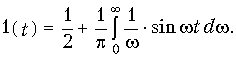
Интеграл в (9.58) можно рассматривать как вещественную форму обратного преобразования Фурье (9.7) для нечетной функции f(t) = 1(t) – 1/2, спектр которой равен 1/w. Тогда на основании (9.58) и с учетом условий (9.52) и (9.56), для выходного сигнала можно записать:

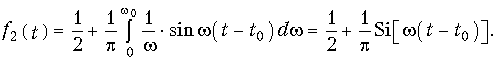
Интеграл в (9.59) табулирован и носит название интегрального синуса: Si[w(t – t₀)]. На рис. 9.16 приведен график сигнала на выходе идеального ФНЧ, определяемой функцией (9.59).

Как следует из представленного графика, чем уже полоса пропускания ФНЧ (меньше w₀), тем меньше крутизна фронта нарастания импульса:df₂/dt = w₀/p. Таким образом, как и в случае единичного импульса для уменьшения искажений выходного сигнала необходимо расширять полосу пропускания ФНЧ. Выбросы в выходном сигнале обусловлены теми же причинами, что и в случае, изображенном на рис. 9.15 (идеализация АЧХ ФНЧ).

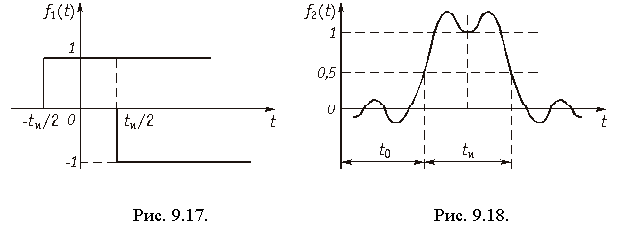
Прямоугольный импульс можно рассматривать как разность двух единичных функций сдвинутых относительно друг друга на t_и/2 (рис. 9.17). Тогда учитывая линейность цепи и равенство (9.59) получим уравнение выходного сигнала для этого случая:

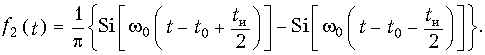
На рис. 9.18 изображен вид выходного сигнала f₂(t), т. е., как и в предыдущих случаях, длительность фронта нарастания и спада импульса обратно пропорциональна полосе пропускания цепи w₀. Чем уже полоса, тем более затянут фронт импульса; чем меньше длительность импульса, тем шире должна быть полоса пропускания цепи. Обычно на практике полосу пропускания выбирают из условия: S_A = 2/t_и.

9.7. Связь между временными и частотными характеристиками электрических цепей

Временной и частотный методы анализа переходных процессов базируются на двух взаимосвязанных характеристиках электрических цепей: импульсной или переходной, с одной стороны, и комплексной передаточной функции, с другой. Между этими характеристиками существует однозначное соответствие. Определим эту связь. Допустим, что на вход пассивной электрической цепи с комплексной передаточной функцией H(jw) приложено воздействие в виде единичной импульсной функции. Тогда с учетом того, что спектр единичного импульсного сигнала равен единице, спектр выходного сигнала согласно (9.51) будет:

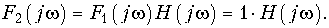
Обратное преобразование (9.7) определит выходной сигнал f₂(t), который численно равен импульсной характеристике цепи:

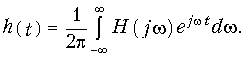
Аналогично с учетом условия физической реализуемости (8.14) можно записать прямое преобразование Фурье:

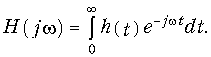
Таким образом, приходим к важному выводу: импульсная и комплексная передаточные функции пассивной электрической цепи связаны между собой парой преобразования Фурье (9.62) и (9.63). А это, в свою очередь, означает, что импульсная характеристика однозначным образом определяет комплексную передаточную функцию цепи и наоборот. Причем, для h(t) и H(jw) справедливы все свойства и теоремы. Основные теоремы спектрального анализа. В частности, из теоремы изменения масштаба независимого переменного следует, что чем более растянута во времени импульсная характеристика цепи, тем уже ее АЧХ и наоборот. Условия безыскаженной передачи сигналов через линейную цепь было показано, что для неискажающей линейной цепи АЧХ должна быть равномерна, а это соответствует согласно (9.40) импульсной характеристике цепи в виде d-функции, что полностью подтверждает изложенное.

Связь комплексной передаточной функции с переходной характеристикой также определяется однозначно, поскольку последняя связана соотношением (8.2) с импульсной характеристикой цепи. Для установления этой связи можно воспользоваться интегральным представлением единичной функции (9.58):

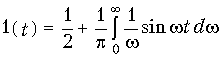
с учетом формулы Эйлера (3.18) перепишем (9.64):

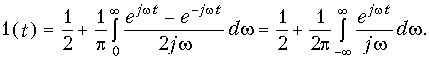
Если ко входу электрической цепи с передаточной функцией H(jw) = |H(jw)|e^jj(w) приложена единичная функция (9.65), то сигнал на выходе цепи будет численно равен переходной характеристики g(t), спектр которой определяется согласно (9.51), где 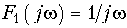. Тогда после применения обратного преобразования Фурье с учетом (9.65) получим:

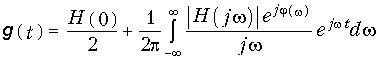
или

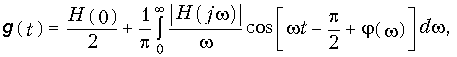
где

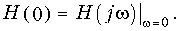
Таким образом, зная Н(jw), можно найти с помощью (9.66) также и g(t). Важно отметить предельное соотношение между g(t) и Н(jw), вытекающее непосредственно из свойств (7.17)—(7.18) и связи между преобразованием Фурье и Лапласа:

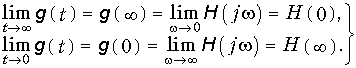
Эти соотношения означают, что реакция на выходе цепи от единичного воздействия в установившемся режиме будет отлична от нуля, если передаточная функция на нулевой частоте не равна нулю (есть путь постоянной составляющей). И напротив, в начальный момент при t = 0 (момент коммутации) реакция на выходе будет изменяться скачком, если Н(¥) — не равна нулю, т. е. цепь имеет бесконечно большую полосу пропускания. Рассмотренные соотношения хорошо иллюстрируются условиями пропускания сигнала через линейную цепь.

В заключение рассмотрим связь между вещественной Н₁(w) и мнимой Н₂(w) частями комплексной передаточной функции (4.7). Перепишем (9.62) в форме

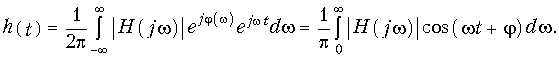
Отсюда, учитывая (4.7) и (4.8), получаем

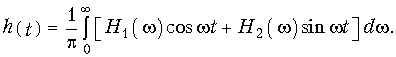
Согласно условия физической реализуемости (8.14) при t < 0 h(t) = 0, поэтому (9.69) принимает вид

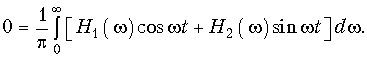
Отсюда, почленно складывая и вычитая (9.69) и (9.70), получаем уравнения связи импульсной характеристики с вещественной и мнимой частями комплексной передаточной функции H(jw):

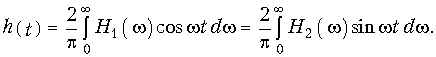
Таким образом, для нахождения импульсной характеристики цепи достаточно воспользоваться частотной зависимостью только вещественной или мнимой частей H(jw). Из (9.71) следует также важный вывод о том, что нельзя независимо выбирать вещественную и мнимую части передаточной функции или, что то же самое, нельзя произвольно выбирать АЧХ и ФЧХ цепи, так как они связаны между собой определенной зависимостью (4.9), (4.10).

9.8. Вопросы и задания для самопроверки

1. Какие существуют методы определения сигнала по спектру?

2. Каким образом можно определить постоянную составляющую единичной функции, если известна спектральная плотность единичной функции?

3. Чем отличаются сигналы с дискретным и сплошным спектрами?

4. В каких случаях используется теорема свертки?

5. Каким образом и зачем определяют полюсы спектральной функции?

6. Что понимают под спектральной плотностью энергии сигнала?

7. Зависит ли спектральная плотность энергии сигнала от формы (вида) сигнала и фазы спектральных составляющих?

8. Как можно получить уравнение единичной функции в интегральной форме 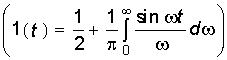, если известно обобщенное преобразование Фурье единичной функции?

9. Как связаны между собой импульсная, переходная и комплексная передаточная функции пассивной электрической цепи?

10. В чем сущность частотного анализа линейных электрических цепей при негармонических воздействиях?

11. Можно ли создать электрическую цепь для безыскаженной передачи сигнала во всем частотном диапазоне?

12. Как связаны между собой комплексная амплитуда и комплексная спектральная плотность?

13. В каких случаях при анализе сигналов применяются интеграл Фурье и ряд Фурье?

14. Каким условиям должен удовлетворять сигнал, подвергаемый преобразованию Фурье?

15. Пояснить физический смысл основных теорем спектрального анализа?

16. Связь между преобразованиями Фурье и Лапласа.