Пусть имеется два дискретных источника с энтропиями H(x) и H(y) и объёмами алфавитов k и l (рис. 2)

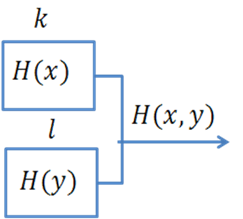
Рис. 2

Объединив оба эти источника в один сложный источник и определим совместную энтропию. Элементарное сообщение на выходе системы содержит элементарное сообщение x_i и сообщение y_i. Алфавит сложной системы будет иметь объём K.L, а энтропия будет равна

(15)

или

(16)

По теореме умножения вероятностей

Подставляя эти соотношения в (15), получим (17)

Аналогично можно получить

(18)

Здесь H(x) и H(y) – собственная энтропия источников x и y

(19)

-условная энтропия источника y относительно источника x. Она показывает, какую энтропию имеют сообщения y, когда уже известно сообщения x.

Если источники независимы, то

P(y/x)=P(y) и H(y/x)=H(y). В этом случае H(x,y)=H(x)+H(y).

Если источники частично зависимыми, то H(x,y)<H(x)+H(y).

Если источники полностью зависимыми(x и y – содержат одну и ту же информацию), то H(y/x)=0 и H(x,y)=H(x)=H(y).