10.1. Способы разделения сигналов
10.2. Основы теории линейной селекции
10.3. Комбинационное разделение сигналов
10.4. Принципы кодово-адресного уплотнения
10.1. Способы разделения сигналов
Важной проблемой техники передачи сообщений является увеличение пропускной способности линий связи путем одновременной передачи сообщений по нескольким каналам. Система связи называется многоканальной, если она обеспечивает взаимно независимую передачу нескольких сообщений по одной общей линии связи с применением общего передатчика и приемника. Многоканальная связь получила широкое распространение как на проводных, так и на радиолиниях. Системы наземной и космической телеметрии также обычно являются многоканальными.
Принцип многоканальной связи достаточно прост. Сообщения u![]() (t), u
(t), u![]() (t), ..., un(t), подлежащие передаче, преобразовываются в электрические сигналы s
(t), ..., un(t), подлежащие передаче, преобразовываются в электрические сигналы s![]() (t), s2(t), ..., sn(t), а затем смешиваются в аппаратуре уплотнения (рис. 10.1). Полученный таким образом групповой (линейный) сигнал s(t) передается по линии связи. Формирование канальных сигналов на передающем конце линии производится при помощи модуляторов М
(t), s2(t), ..., sn(t), а затем смешиваются в аппаратуре уплотнения (рис. 10.1). Полученный таким образом групповой (линейный) сигнал s(t) передается по линии связи. Формирование канальных сигналов на передающем конце линии производится при помощи модуляторов М![]() и соответствующим образом подобранных переносчиков
и соответствующим образом подобранных переносчиков ![]() (t)- Канальные сигналы отличаются друг от друга не только передаваемыми сообщениями, но и их переносчиками. На приемном конце сигнал x(t)=s(t)+ω(t) поступает на систему разделителей Ф
(t)- Канальные сигналы отличаются друг от друга не только передаваемыми сообщениями, но и их переносчиками. На приемном конце сигнал x(t)=s(t)+ω(t) поступает на систему разделителей Ф![]() , которые выделяют сигналы соответствующих каналов. После разделения канальные сигналы
, которые выделяют сигналы соответствующих каналов. После разделения канальные сигналы ![]() (t),
(t), ![]() (t), ...,
(t), ..., ![]() (t) преобразовываются в сообщения
(t) преобразовываются в сообщения ![]() (t),
(t), ![]() (t), ...,
(t), ..., ![]() (t), поступающие к получателю.
(t), поступающие к получателю.
Операции, производимые над сигналами в многоканальной системе связи, показанной на рис. 10.1, можно аналитически записать в следующем виде:
— операция формирования канальных сигналов
![]() (10.1)
(10.1)
где М![]() — оператор, описывающий действия преобразователя М
— оператор, описывающий действия преобразователя М![]() ;
;
— операция формирования группового сигнала
![]() (10.2)
(10.2)
В частном случае
![]()
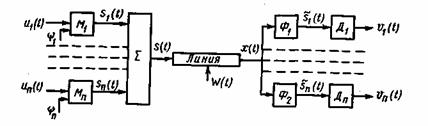
Рис 10.1. Система многоканальной связи
— операция разделения канальных сигналов
![]() (10.3)
(10.3)
где Ф![]() — оператор k-то разделителя, ω(t)— аддитивная помеха;
— оператор k-то разделителя, ω(t)— аддитивная помеха;
— операция восстановления переданного сообщения
![]() (10.4)
(10.4)
Здесь ![]() —оператор, описывающий действие k-то детектора.
—оператор, описывающий действие k-то детектора.
В идеальной системе при отсутствии помех и искажений, когда ![]() , принятый сигнал преобразуется в сообщение обратным оператором
, принятый сигнал преобразуется в сообщение обратным оператором ![]() , т. е.
, т. е.
![]()
В этом случае принятое сообщение тождественно переданному.
Основную проблему многоканальной связи составляет задача разделения канальных сигналов. Практически разделение не бывает совершенным: на сигнал одного канала накладываются в той или иной мере сигналы других каналов. Это создает специфические для многоканальной связи переходные или взаимные помехи. Улучшением системы разделения эти помехи могут быть сведены до допустимой величины.
Для разделения сигналов на приемном конце, очевидно, необходимо, чтобы они различались между собой по некоторому признаку и чтобы разделители могли осуществить разделение на основе этого признака. Вид отличительного признака канальных сигналов определяет систему разделения. В практике многоканальной связи преимущественное применение имеют частотный и временной способы разделения сигналов.
При частотном разделении сигналы различных каналов размещаются в не перекрывающихся частотных полосах. На приемном конце эти сигналы выделяются с помощью фильтров. Для того чтобы разместить спектры нескольких низкочастотных сообщений (например, телефонных) в не перекрывающихся частотных полосах, необходимо, чтобы несущие колебания (переносчики) в различных каналах имели различные частоты. Эти колебания модулируются передаваемыми сообщениями по одному из параметров (амплитуде, частоте или фазе).

Рис. 10.2. Спектры передаваемых сообщений (а) и группового сигнала (б)
Несущие частоты должны быть разнесены на интервал, равный ширине спектра модулированного колебания. При обычной AM интервал между несущими частотами должен равняться удвоенной ширине спектра низкочастотного сигнала (сообщения). Очевидно, наилучшее уплотнение по частоте можно' получить, применяя однополосную модуляцию (ОМ). В этом случае интервал между каналами будет иметь минимально возможную величину, равную ширине спектра передаваемого сообщения. На рис. 10.2а показан спектр передаваемых сообщений, а на рис. 10.2б — спектр группового сигнала при амплитудной модуляции несущих.
В технике радиосвязи, для частотного уплотнения каналов применяется двойная модуляция. В этом случае передаваемыми сообщениями модулируются поднесущие колебания с различными частотами ![]() . Число поднесущих выбирается равным числу каналов. Совокупность (сумма) модулированных поднесущих образует групповой сигнал, которым затем модулируется несущая с частотой
. Число поднесущих выбирается равным числу каналов. Совокупность (сумма) модулированных поднесущих образует групповой сигнал, которым затем модулируется несущая с частотой ![]() . На приеме вначале детектируется несущая и выделяется групповой сигнал. Затем при помощи фильтров из этого сигнала выделяются канальные сигналы, представляющие собой поднесущие, промодулированные передаваемыми сообщениями. Наконец, детектирование канальных сигналов позволяет выделить сообщение на выходе каждого канала.
. На приеме вначале детектируется несущая и выделяется групповой сигнал. Затем при помощи фильтров из этого сигнала выделяются канальные сигналы, представляющие собой поднесущие, промодулированные передаваемыми сообщениями. Наконец, детектирование канальных сигналов позволяет выделить сообщение на выходе каждого канала.
Системы с поднесущими находят широкое применение в радиорелейных линиях связи и в телеметрии. Помехоустойчивость и эффективность систем с поднесущими зависит от вида модуляции как поднесущей, так и несущей. Возможный выбор здесь достаточно большой: АМ-АМ, АМ-ЧМ, ОМ-ЧМ, АМ-ФМ и т. д. При оценке помехоустойчивости этих систем следует учитывать наряду с аддитивными помехами переходные помехи.
Исследования показывают, что широко распространенная в радиорелейных линиях связи система ОМ-ЧМ обеспечивает сравнительно высокую помехоустойчивость при малом уровне помех. С увеличением индекса модуляции заметно снижается эффективность использования полосы частот. К недостаткам системы ОМ-ЧМ следует также отнести наличие порога помехоустойчивости и появление переходных помех при многолучевом распространении радиоволн.
Привлекает внимание система ОМ-ОМ. Она обеспечивает высокую эффективность, не имеет порога и свободна от переходных помех за счет многолучевого распространения радиоволн.
Многоканальная радиотелеграфная связь применяется и в диапазоне коротких волн. Здесь обычно используется система с поднесущими ЧМ-ОМ или ОФМ-ОМ при сравнительно небольшом числе каналов.
На укв и в радиорелейных линиях связи для телеграфной передачи выделяется часть телефонных каналов, которые, в свою очередь, уплотняются телеграфными каналами.
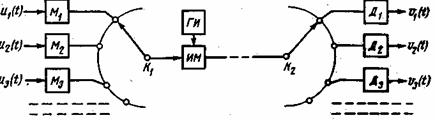
Рис. 10.3. Система с временным разделением каналов
На рис. 10.3 приведена структурная схема системы многоканальной связи с временным разделением каналов. Основу системы составляют два синхронно работающих коммутатора ![]() и
и ![]() - На передающей стороне к ламелям коммутатора
- На передающей стороне к ламелям коммутатора ![]() подводятся канальные сигналы от входных преобразователей. Вращающаяся щетка коммутатора
подводятся канальные сигналы от входных преобразователей. Вращающаяся щетка коммутатора ![]() поочередно подключает каждый из преобразователей на вход импульсного модулятора ИМ-устройства, осуществляющего модуляцию импульсной последовательности, поступающей в него от генератора импульсов ГИ. Импульсы, модулированные сообщениями всех каналов, поступают в линию связи, а затем на коммутатор
поочередно подключает каждый из преобразователей на вход импульсного модулятора ИМ-устройства, осуществляющего модуляцию импульсной последовательности, поступающей в него от генератора импульсов ГИ. Импульсы, модулированные сообщениями всех каналов, поступают в линию связи, а затем на коммутатор ![]() , являющийся разделителем каналов на приеме. Коммутатор
, являющийся разделителем каналов на приеме. Коммутатор ![]() подключает каждый входной преобразователь в момент, когда по каналу связи поступает импульс данного канала. Важно, чтобы в такой системе коммутаторы
подключает каждый входной преобразователь в момент, когда по каналу связи поступает импульс данного канала. Важно, чтобы в такой системе коммутаторы ![]() и
и ![]() работали синхронно. Для синхронизации обычно передают вспомогательные синхронизирующие импульсы, для которых отводится один или несколько каналов.
работали синхронно. Для синхронизации обычно передают вспомогательные синхронизирующие импульсы, для которых отводится один или несколько каналов.
Для наглядности мы описали систему с механическими коммутаторами. В действительности применяются электронные коммутаторы.
При временном разделении каналов применяются различные способы импульсной модуляции, которые были рассмотрены в гл. 3.
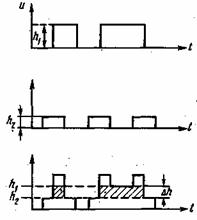
Рис. 10.4. Принцип разделения сигналов по уровню
В настоящее время находят применение ФИМ, ШИМ, ИКМ и др.
При фазовом разделении попользуется различие сигналов по фазе. Такое разделение осуществляется посредством синхронного детектирования.
Разделение по форме. В тех случаях, когда сигналы передаются одновременно, и их спектры перекрываются, разделение сигналов осуществляется по признакам, характеризующим их форму. Простейшим примером разделения сигналов по форме является метод разделения по уровню (рис. 10.4).
Пусть имеется два канала, сигналы которых представляют собой произвольную временную последовательность импульсов,
имеющих высоту ![]() в первом канале и
в первом канале и ![]() —во втором. Такие сигналы принципиально всегда могут быть разделены при условии
—во втором. Такие сигналы принципиально всегда могут быть разделены при условии ![]() . Разделение можно осуществить, например, так. Если
. Разделение можно осуществить, например, так. Если ![]() , первый сигнал выделяется при помощи ограничения смеси двух сигналов снизу да уровне
, первый сигнал выделяется при помощи ограничения смеси двух сигналов снизу да уровне ![]() , а сверху на уровне
, а сверху на уровне ![]() т. е. путем вырезания из смеси полосы высотой
т. е. путем вырезания из смеси полосы высотой ![]() .
.
В результате такого ограничения сигнал первого канала выделяется в чистом виде. Для выделения сигнала второго канала можно увеличить полученный сигнал первого канала в ![]() раз и вычесть его из смеси обоих сигналов.
раз и вычесть его из смеси обоих сигналов.
Методы разделения сигналов по форме лежат в основе построения широкополосных систем связи с шумоподобными сигналами.
10.2. Основы теории линейной селекции
Эффективное разделение сигналов может быть осуществлено только на основе строгой теории, в которой формулируются условия разделения и даются количественные оценки различных способов разделения. Возможны два подхода к решению этой проблемы: геометрический и аналитический. С принципиальной точки зрения оба эти подхода равноценны. Геометрическая теория различения (разделения) сигналов была рассмотрена в § 2.11. Ниже рассматривается аналитическая теория разделения (линейной селекции). Основы этой теории были разработаны Д. В. Агеевым в 1935 г.
Пусть канальные сигналы записаны в виде
![]() (10.5)
(10.5)
где ![]() — переносчик, а
— переносчик, а ![]() — коэффициент, отображающий передаваемое сообщение по k-му каналу. Произведение
— коэффициент, отображающий передаваемое сообщение по k-му каналу. Произведение ![]() представляет результат модуляции переносчика
представляет результат модуляции переносчика ![]() сообщением
сообщением ![]() . Различие между канальными сигналами — это различие между переносчиками
. Различие между канальными сигналами — это различие между переносчиками ![]() .
.
Линейный сигнал представляет собой сумму канальных сигналов
![]() (10.6)
(10.6)
Этот сигнал передается по линии связи. На приемном конце для разделения сигналов имеется п разделительных (избирательных) устройств. Действие этих устройств будем описывать оператором разделения ![]() . Далее мы предполагаем, что помехи в канале отсутствуют.
. Далее мы предполагаем, что помехи в канале отсутствуют.
Сущность разделения состоит в том, что каждое из избирательны устройств должно реагировать на «свой» сигнал и не реагировать на все остальные. Математически это запишется в виде
![]() (10.7)
(10.7)
где
![]()
Необходимым и достаточным условием разделимости сигналов ![]() является
является
условие их линейной независимости, которое состоит в том, что тождество
![]() (10.8)
(10.8)
удовлетворяется только в том единственном случае, когда все коэффициенты одновременно равны нулю.
Линейно-независимой называется такая система функций ![]() , при которой ни одна из них не может быть выражена в виде линейной комбинации остальных. Если можно подобрать такие не равные нулю значения
, при которой ни одна из них не может быть выражена в виде линейной комбинации остальных. Если можно подобрать такие не равные нулю значения ![]() , что тождество (10.8) удовлетворяется, то функции
, что тождество (10.8) удовлетворяется, то функции ![]() зависимы. Действительно, если, например,
зависимы. Действительно, если, например, ![]() и
и ![]() не равны нулю, то при
не равны нулю, то при ![]() функция
функция ![]() есть с масштабным множителем
есть с масштабным множителем![]() .
.
Большой практический интерес представляет случай, когда канальные сигналы образуют ортогональную систему функций ![]() , что является достаточным, но не необходимым условием для их разделимости. Условие ортогональности записывается в виде
, что является достаточным, но не необходимым условием для их разделимости. Условие ортогональности записывается в виде
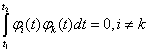 (10.9)
(10.9)
Будем считать, кроме того, что функции ![]() нормированы так, что
нормированы так, что
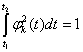 (10.10)
(10.10)
Линейный сигнал пусть представляется суммой
![]() (10.11)
(10.11)
При этих условиях разделение сигналов сводится к нахождению коэффициентов разложения s(t) по ортогональным нормированным функциям ![]() . Умножая (10.11) на
. Умножая (10.11) на ![]() и интегрируя, получим
и интегрируя, получим
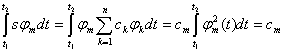
Следовательно, оператор разделения Фтв этом случае имеет вид
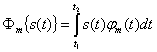 (10.12)
(10.12)
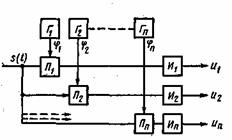
Рис. 10.5. Схема разделения ортогональных сигналов
Результатом этой операции является выделение величины ст, т. е. сообщения соответствующего канала.
Структурная схема устройства, разделяющего ортогональные сигналы, показана на рис. 10.5. Она состоит из п корреляторов, каждый из которых выделяет соответствующий сигнал и восстанавливает переданное сообщение.
Общая теория, изложенная выше, есть в сущности, теория разделения сигналов по форме. Известные способы разделения по частоте, фазе и по времени являются частными случаями этого общего метода разделения.
В случае фазового разделения канальные сигналы с учетом нормировки запишутся в виде:
![]()
Линейный сигнал представляется суммой
![]()
Разделение происходит следующим образом:
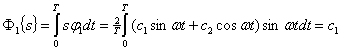
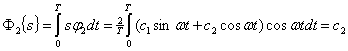
При временном разделении по линии в любой момент времени передается только один сигнал. Поэтому условие линейной независимости (10.8) вырождается в равенство ![]() , а это возможно только при
, а это возможно только при ![]() . Оператором разделения k-го канала
. Оператором разделения k-го канала ![]() в данном случае является временная характеристика коммутатора K, равная единице при замыкании и нулю при размыкании(рис. 10.3).
в данном случае является временная характеристика коммутатора K, равная единице при замыкании и нулю при размыкании(рис. 10.3).
При частотном разделении условие линейной независимости канальных сигналов вытекает из того, что сигналы занимают не перекрывающиеся полосы частот. Оператором разделения k-гo канала ![]() является фильтр, который пропускает только частоты этого канала и совершенно не пропускает частоты всех других каналов.
является фильтр, который пропускает только частоты этого канала и совершенно не пропускает частоты всех других каналов.
Система линейно-зависимых функций, как известно, может быть ортогонализована, т. е. путем линейного преобразования заманена системой ортогональных функций. Следовательно, разделение линейно-независимых сигналов всегда можно свести к разделению ортогональных функций.
10.3. Комбинационное разделение сигналов
Пусть имеются два канала и пусть оба канала работают двоичным кодом с элементами 0 и 1. Тогда возможны следующие комбинации сигналов в обоих каналах (табл. 10.1).
Как видим, если сигналы обоих каналов будут смешаны, то разделить их невозможно. Но мы можем вместо суммарного сигнала, передавать номер комбинации, так как этот номер однозначно определяет сигналы каждого из каналов в отдельности. Таким образом, дело сводится к передаче чисел. Эти числа могут быть переданы любым способом, т. е. закодированы любым кодом и переданы посредством любого вида модуляции.
Построение многоканальной системы сводится к созданию некоторого устройства, на n входов которого поступают сигналы п каналов и которое вырабатывает посылаемый в линию линейный сигнал в форме кодовой комбинации, отображающей совокупность мгновенных значений канальных сигналов в данный момент. Число таких комбинаций равно, очевидно, N=mn, где n— число каналов, а m— основание кода в канале до преобразования.
Таблица 10.1
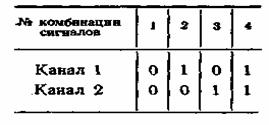
Таким образом, линейный сигнал не просто есть сумма или смесь канальных сигналов, а представляет собой отражение определенной комбинации канальных сигналов, горючем выбор способа отображения зависит от нашего усмотрения. Такой способ разделения сигналов называется комбинационным разделением.
Примерами систем с комбинационным разделением каналов являются двухканальная система частотного телеграфирования (ДЧТ) и двухканальная система фазового телеграфирования (ДФТ). В системе ДЧТ в качестве сигналов используются колебания четырех различных частот, несущие информацию в значениях символов в каждом из двух бинарных каналов. В системе ДФТ символы двух каналов передаются с помощью отрезков гармонических колебаний одной частоты, но с различными значениями начальной фазы. Комбинационный метод разделения применяется в многоканальных системах с числом каналов 2—4. При числе каналов больше двух полоса частот, занимаемая системой, при комбинационном уплотнении шире, чем при частотном или временном способе и эта разница быстро возрастает с увеличением числа каналов.
10.4. Принципы кодово-адресного уплотнения
В системах с кодово-адресным разделением каждому абоненту (станции) присваивается адрес, представляющий собой определенную кодовую последовательность. На приемном конце эти последовательности должны быть известны всем абонентам. Такие системы позволяют осуществить связь между большим числом абонентов, используя общую полосу частот, причем каждый абонент может немедленно вызвать любого другого абонента.
Примером таких систем может быть асинхронная адресная система связи (ААСС). В этой системе каждый информационный элемент передаваемого сообщения кодируется с помощью набора сигналов, специально подобранных для каждого абонента. Приемное устройство выделяет сигналы, предназначенные для данного абонента и не реагирует на сигналы других абонентов. Число абонентов может быть произвольно большим. Ограничивается число одновременно устанавливаемых связей. Если это граничное число превышается, то появляются взаимные помехи.
Взаимные помехи в системах с адресным уплотнением являются основным фактором, ограничивающим скорость передачи информация, поэтому проблема выбора сигналов здесь является основной. Необходимо найти большой ансамбль сигналов, имеющих «хорошие» корреляционные свойства и, прежде всего, малые значения взаимокорреляционной функции. Такие сигналы часто называют квазиортогональными. В системах с кодово-адресным уплотнением используются как непрерывные, так и дискретные по времени и частоте сигналы.
В системах с непрерывными сигналами могут быть использованы либо реальные образцы шума, либо двоичные псевдослучайные последовательности. Можно, например, в качестве сигнального алфавита использовать набор псевдошумовых сигналов, сдвинутых, по частоте.
Речевые сигналы, передаваемые системой, кодируются с помощью этого алфавита и передаются к различным абонентам по общей полосе частот. Сигнал в этом случае можно записать в виде
![]() (10.13)
(10.13)
где exp[iφ(t)]=(+1,-1,-1,…) —псевдошумовой сигнал длительностью Т, представляющий собой двоичную псевдослучайную последовательность, состоящую из N импульсов; ![]() частотный сдвиг,
частотный сдвиг, ![]() — несущая частота,
— несущая частота, ![]() — число импульсов а сигнале,
— число импульсов а сигнале, ![]() полоса частот сигнала.
полоса частот сигнала.
Каждому абоненту ставится в соответствие определенный частотный сдвиг. В приемнике из общей суммы сигналов с помощью соответствующей их обработки (коррелятора, например, или согласованных фильтров) выделяется тот сигнал, который ему предназначен. Передаваемое непрерывное сообщение предварительно подвергается дискретизации, кодируется с помощью алфавита адресных псевдошумовых сигналов и передается по линии связи. В приемнике сигнал поступает на детектор огибающей, в решающее устройство и далее в фильтр, восстанавливающий переданное непрерывное сообщение.
Во многих системах с кодово-адресным уплотнением используется в качестве сигналов набор элементов частотно-временной матрицы (рис. 10.6). В этих системах с помощью дельта-модуляции или фазово-импульсной модуляции непрерывные сигналы преобразуются из аналоговой формы в последовательность импульсов определенной длительности. Формирующее устройство в передатчике кодирует каждый двоичный информационный знак в дискретный адрес — набор импульсов на различных частотах. Каждый информационный импульс передается с помощью трех-четырех коротких посылок несущей частоты. Изменение временного промежутка между импульсами и частотная селекция посылок несущей дают несколько тысяч различных время частотных адресных комбинаций. Перед демодулятором приемника находится устройство опознавания адреса. Дискретные адреса пропускаются в заранее установленные промежутки времени на предварительно выбранных частотах. Выходное устройство преобразует принимаемые сигналы в речь.
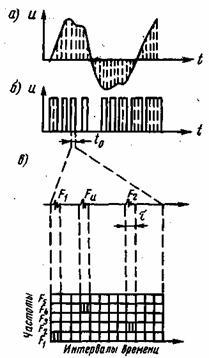
Рис. 10.6. Принцип формирования сигнала в дискретно-адресной системе
Важным достоинством систем с кодово-адресным уплотнением являются повышенная надежность и меньшая стоимость оборудования по сравнению с системами с частотным уплотнением. Здесь используются менее сложные эталоны частот, не требуются дорогостоящие канальные фильтры. Приемник в этих системах работает как цифровой согласованный фильтр.
Следует отметить, что кодово-адресное разделение, так же как и комбинационное, не является новым видом селекции. Здесь в различных сочетаниях используются те же при основных вида линейной селекции: по частоте времени и форме сигнала.
10.5. Взаимные помехи при разделении сигналов
Можно показать, что идеальное разделение сигналов практически невозможно. Условия разделения (10.8) или (10.9) не могут быть строго выполнены. Поэтому всегда появляются взаимные влияния каналов, состоящие в появлении на выходе данного канала часта сигналов соседних каналов. Эти влияния проявляются в виде взаимных или переходных помех, снижающих пропускную способность каналов.
Основными причинами появления взаимных помех являются: 1) погрешность при формировании сигналов заданной формы на передающем конце; 2) искажения сигналов, вносимые самой линией; 3) несовершенство разделяющих устройств.
Так, при частотном разделении сигналов исходят из того, что сигнал данного канала занимает ограниченную полосу частот и что на приеме имеется фильтр, способный выделить эту полосу. Но реальный сигнал всегда имеет конечную длительность и, следовательно, должен иметь спектр бесконечной протяженности. Таким образом, локализация спектра сигнала конечной длительности в конечной полосе частот принципиально невозможна. Если же мы искусственно ограничим спектр сигнала, то появятся искажения. Кроме того, реализовать идеальный фильтр, т. е. фильтр с бесконечно большим затуханием вне полосы пропускания, практически невозможно.
Аналогичные трудности возникают и при временном разделении. Здесь предполагается, что каждый элемент сигнала локализован по времени в пределах некоторого интервала и имеет вид импульса, равного нулю вне этого интервала. Но импульс конечной длительности имеет бесконечно широкий спектр, который не; может быть передан по каналу связи с ограниченной полосой пропускания. Результатом ограничения спектра является расплывание импульсов во времени. При этом часть энергии импульса попадает в соседние интервалы. Таким образом, и при этом способе разделения возникают переходные помехи.
Для обеспечения хорошего качества передачи приходится оставлять запасные интервалы как по частоте, так и по времени с тем, чтобы снизить переходные помехи до допустимого уровня.
10.6. Пропускная способность систем многоканальной связи
Мы установили, что в реальных условиях ни сигналы, ни разделяющие устройства не удовлетворяют требованиям идеального разделения. Вследствие этого в многоканальных системах связи наряду с аддитивными помехами всегда имеют место взаимные помехи от соседних каналов. При большем числе каналов характер этих помех можно считать близким к флуктуационным шумам.
Средняя мощность переходных помех в канале пропорциональна средней мощности сигнала и равна λРС, где λ — коэффициент взаимного мешающего действия между каналами.,
Общая мощность помех в канале равна сумме аддитивной ![]() и переходной λРСпомех:
и переходной λРСпомех: ![]() . Эту мощность, очевидно, и следует подставлять в формулу Шеннона (6.87) при определении пропускной способности канала:
. Эту мощность, очевидно, и следует подставлять в формулу Шеннона (6.87) при определении пропускной способности канала:
![]() (10.14)
(10.14)
Пропускная способность всей системы будет равна:
![]() (10.15)
(10.15)
Из ф-л (10.14) и (10.15) следует, что пропускная способность многоканальной системы увеличивается при уменьшения λ, т. е. при улучшении качества разделения каналов.
В случае малого уровня аддитивных помех по сравнению с переходными, т. е. при ![]() .имеем
.имеем
![]() (10.16)
(10.16)
В этом случае при заданном качестве разделения увеличить пропускную способность канала за счет увеличения мощности сигналов не представляется возможным.
Для того чтобы взаимные помехи не приводили к заметному снижению пропускной способности системы связи, необходимо добиваться такого значения коэффициента λ, при котором ![]() , т. е.
, т. е. ![]() .
.
Вопросы для повторения
1. Для чего применяются многоканальные линии связи?
2. Перечислите основные методы уплотнения каналов.
3. Как строится система с частотным разделением каналов?
4. Как строится система с временным разделением каналов?
5. Каковы причины переходных помех при частотном и при временном уплотнениях?
6. Сформулируйте общее условие разделения сигналов по форме.
7. Приведите схему разделения ортогональных сигналов.
8. Покажите, что сигналы в системах с частотным и временным уплотнениями удовлетворяют условию ортогональности.
9. В каких системах используется разделение сигналов по форме? 10. Поясните принцип комбинационного уплотнения.
11. Какие системы комбинационного уплотнения применяются в настоящее время?
12. Поясните принцип кодово-адресного уплотнения.
13. Дайте сравнительную оценку систем частотного и временного уплотнений.
14. Как определяется пропускная способность многоканальных систем связи?
Список основных обозначений и формул
![]() — амплитуда сигнала
— амплитуда сигнала
ŋ![]() — коэффициент использования мощности сигнала
— коэффициент использования мощности сигнала
Bx(t)— функция корреляции процесса x(t)
ŋ![]() — коэффициент использования полосы частот канала
— коэффициент использования полосы частот канала
D[x(t)]— дисперсия случайного процесса x(t)
v=2TF— база сигнала
Е — энергия сигнала
ρ(τ)—нормированная функция автокорреляции
F — ширина спектра сигнала
F(x)—интегральная функция распределения случайной величины х
ρ![]() — коэффициент взаимной корреляции
— коэффициент взаимной корреляции
σ![]() — среднеквадратическое значение случайной величины х
— среднеквадратическое значение случайной величины х
Fm — наивысшая частота сообщения
f — частота
τ![]() — длительность импульса
— длительность импульса
G![]() (ω)— энергетический спектр процесса x(t)
(ω)— энергетический спектр процесса x(t)
Δτ— интервал корреляции
ω— угловая частота
Н— энтропия
l(s,х)— количество информации, содержащейся в принятом сигнале х относительно переданного сигнала s
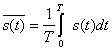 — среднее значение колебания s(t)
— среднее значение колебания s(t)
K(f) — коэффициент передачи на частоте f
![]() k
k![]() ‑ коэффициенты, зависящие от формы сигнала
‑ коэффициенты, зависящие от формы сигнала
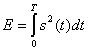 ‑ энергия сигнала
‑ энергия сигнала
k![]() — пикфактор
— пикфактор
m— основание кода
N![]() — удельная мощность помехи
— удельная мощность помехи
Р![]() ‑ средняя мощность сигнала
‑ средняя мощность сигнала
P![]() — средняя мощность помехи
— средняя мощность помехи
P![]() — вероятность ошибки
— вероятность ошибки
ρ(х) — плотность вероятности случайной величины х
R— скорость передачи информации в дв.ед./сек
q — отношение средних мощностей сигнала и помехи
q![]() — отношение энергии сигнала к удельной мощности помехи
— отношение энергии сигнала к удельной мощности помехи
s(t),s(u,t)— переданный сигнал
S![]() (iω)‑ спектральная плотность процесса x(t)
(iω)‑ спектральная плотность процесса x(t)
Т- длительность сигнала, период разложения сигнала в ряд
t![]() — период повторения импульсов
— период повторения импульсов
t— время
u(t) — переданное сообщение
v(t) принятое сообщение
ω(t) — аддитивная помеха
x(t)‑ принятый сигнал (суммарное колебание сигнала и помехи)
α![]() ‑ коэффициент, пропорциональный отношению энергии сигнала к удельной мощности помехи
‑ коэффициент, пропорциональный отношению энергии сигнала к удельной мощности помехи
γ![]() ‑ выигрыш системы
‑ выигрыш системы
ε— среднеквадратическая ошибка
η‑ коэффициент (эффективность) использования канала
q![]() =
=![]() =
=![]() ,
,
q=![]() ,
,
α![]() =(1-ρ
=(1-ρ![]() )q
)q![]() =TF(1-ρ
=TF(1-ρ![]() )q,
)q,
Φ(x)=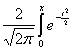 dt,
dt,
F(x)=![]()
Горизонтальная черта обозначает статистическое среднее
![]() ,где интеграл берется по всей области определения х
,где интеграл берется по всей области определения х
Волнистая черта обозначает усреднение по времени
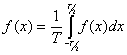
АМ‑ амплитудная модуляция
БМ‑ балансная модуляция
ОМ‑ однополосная модуляция
ФМ‑ фазовая модуляция
ЧМ‑ частотная модуляция
ШИМ‑ широтно-импульсная модуляция
АИМ— амплитудно-импульсная модуляция
ИКМ—импульсно-кодовая модуляция
ЧИМ— частотно-импульсная модуляция
ФИМ‑ фазово-импульсная модуляция
ДМ‑ дельта-модуляция
Приложение 1. Таблица функции Крампа
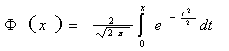
|
X |
Ф(х) |
X |
Ф(х) |
X |
Ф(х) |
X |
Ф(х) |
||||||
|
0,00 |
0,0000 |
0,25 |
0,1974 |
0,50 |
0,3829 |
0,75 |
0,5467 |
||||||
|
01 |
0,0080 |
26 |
0,2051 |
51 - |
0,3899 |
76 |
0,5527 |
||||||
|
02 |
0,0160 |
27 |
0,2128 |
52 |
0,3969 |
77 |
0,5587 |
||||||
|
03 |
0,0239 |
28 |
0,2205 |
53 |
0,4039 |
78 |
0,5646 |
||||||
|
04 |
0,0319 |
29 |
0,2282 |
54 |
0,4108 |
79 |
0,5705 |
||||||
|
05 |
0,0399 |
0,30 |
0,2358 |
55 |
0,4177 |
0,80 |
0,5763 |
||||||
|
06 |
0,0478 |
31 |
0,2434 |
56 |
0,4245 |
81 |
0,5821 |
||||||
|
07 |
0,0558 |
32 |
0,2510 |
57 |
0,4313 |
82 |
0,5878 |
||||||
|
08 |
0,0638 |
33 |
0,2586 |
58 |
0,4381 |
83 |
0,5935 |
||||||
|
09 |
0,0717 |
34 |
0,2661 |
59 |
0,4448 |
84 |
0,5991 |
||||||
|
0,10 |
0,0797 |
35 |
0,2737 |
0,60 |
0,4515 |
85 |
0,6047 |
||||||
|
11 |
0,0876 |
36 |
0,2812 |
61 |
0,4581 |
86 |
0,6102 |
||||||
|
12 |
0,0955 |
37 |
0,2886 |
62 |
0,4647 |
87 |
0,6157 |
||||||
|
13 |
0,1034 |
38 |
0,2961 |
63 |
0,4713 |
88 |
0,6211 |
||||||
|
14 |
0,1113 |
39 |
0,3035 |
64 |
0,4778 |
89 |
0,6265 |
||||||
|
15 |
0,1192 |
0,40 |
0,3108 |
65 |
0,4843 |
0 90 |
0,6319 |
||||||
|
16 |
0,1271 |
41 |
0,3182 |
66 |
0,4907 |
91 |
0,6372 |
||||||
|
17 |
0,1350 |
42 |
0,3255 |
67 |
0,4971 |
92 |
0,6 24 |
||||||
|
18 |
0,1428 |
43 |
0,3328 |
68 |
0,5035 |
93 |
0,6476 |
||||||
|
19 |
0,1507 |
44 |
0,3401 |
69 |
0,5098 |
94 |
0,6528 |
||||||
|
0,20 |
0,1585 |
45 |
0,3473 |
0,70 |
0,5161 |
95 |
0,6579 |
||||||
|
21 |
0,1663 |
46 |
0,3545 |
71 |
0,5223 |
% |
0,6629 |
||||||
|
22 |
0,1741 |
47 |
0,3616 |
72 |
0,5285 |
97 |
0,6680 |
||||||
|
23 |
0,1819 |
48 |
0,3688 |
73 |
0,5346 |
98 |
0,6729 |
||||||
|
24 |
0,1897 |
49 |
0,3759 |
74 |
0,5407 |
99 |
0,6778 |
||||||
|
0,25 |
0,1974 |
0,50 |
0,3829 |
0,75 |
0,5467 |
1,00 |
0,6827 |
||||||
|
1,00 |
0,6827 |
1,35 |
0,8230 |
1,70 |
0,9109 |
2,25 |
0,9756 |
||||||
|
01 |
0,6875 |
36 |
0,8262 |
71 |
0,9127 |
30 |
0,9786 |
||||||
|
02 |
0,6923 |
37 |
0,8293 |
72 |
0,9146 |
35 |
0,9812 |
||||||
|
03 |
0,6970 |
38 |
0,8324 |
73 |
0,9164 |
40 |
0,9836 |
||||||
|
04 |
0,7017 |
39 |
0,8355 |
74 |
0,9181 |
45 |
0,9857 |
||||||
|
05 |
0,7063 |
1,40 |
0,8385 |
75 |
0,9199 |
2,50 |
0,9876 |
||||||
|
06 |
0,7109 |
41 |
0,8415 |
76 |
0,9216 |
55 |
0,9892 |
||||||
|
07 |
0,7154 |
42 |
0,8444 |
77 |
0,9233 |
60 |
0,9907 |
||||||
|
08 |
0,7199 |
43 |
0,8473 |
78 |
0,9249 |
65 |
0,9920 |
||||||
|
09 |
0,7243 |
44 |
0,8501 |
79 |
0,9265 |
70 |
0,9931 |
||||||
|
1.10 |
0,7287 |
45 |
0,8529 |
1,80 |
0,9281 |
75 |
0,9940 |
||||||
|
11 |
0,7330 |
46 |
0,8557 |
81 |
0,9297 |
80 |
0,9949 |
||||||
|
12 |
0,7373 |
47 |
0,8557 |
82 |
0,9312 |
85 |
0,9956 |
||||||
|
13 |
0,7415 |
48 |
0,8611 |
83 |
0,9327 |
90 |
0,9963 |
||||||
|
14 |
0,7457 |
49 |
0,8638 |
84 |
0,9342 |
95 |
0,9968 |
||||||
|
15 |
0,7499 |
1,50 |
0,8664 |
85 |
0,9357 |
3,00 |
0,99730 |
||||||
|
16 |
0.7540 |
51 |
0,8690 |
86 |
0,9371 |
10 |
0,99806 |
||||||
|
17 |
0,7580 |
52 |
0,8715 |
87 |
0,9385 |
20 |
0,99863 |
||||||
|
18 |
0,7620 |
53 |
0,8740 |
88 |
0,9399 |
30 |
0,99903 |
||||||
|
19 |
0,7660 |
54 |
0,8764 |
89 |
0,9412 |
40 |
0,99933 |
||||||
|
1.20 |
0,7699 |
55 |
0,8789 |
1,90 |
0,9426 |
50 |
0,99953 |
||||||
|
21 |
0,7737 |
56 |
0,8812 |
91 |
0,9439 |
60 |
0,99968 |
||||||
|
22 |
0,7775 |
57 |
0,8836 |
92 |
0,9451 |
70 |
0,99978 |
||||||
|
23 |
0,7813 |
58 |
0,8859 |
93 |
0,9464 |
80 |
0,99986 |
||||||
|
24 |
0,7850 |
59 |
0,8882 |
94 |
0,9476 |
90 |
0,99990 |
||||||
|
25 |
0,7887 |
1,60 |
0,8904 |
95 |
0,9488 |
4,00 |
0,99994 |
||||||
|
26 |
0,7923 |
61 |
0,8926 |
96 |
0,9500 |
||||||||
|
27 |
0,7959 |
62 |
0,8948 |
97 |
0,9512 |
||||||||
|
28 |
0,7995 |
63 |
0,8969 |
98 |
0,9523 |
4,417 |
1— |
||||||
|
29 |
0,8029 |
64 |
0,8990 |
99 |
0,9534 |
4,892 |
1—10 |
||||||
|
1.30 |
0,8064 |
65 |
0,9011 |
2,00 |
0,9545 |
||||||||
|
31 |
0,8098 |
66 |
0.9031 |
05 |
0,9596 |
5,327 |
1—10 |
||||||
|
32 |
0,8132 |
67 |
0,9051 |
10 |
0,9643 |
||||||||
|
33 |
0,8165 |
68 |
0,9070 |
15 |
0,9684 |
||||||||
|
34 |
0,8198 |
69 |
0,9090 |
20 |
0,9722 |
||||||||
|
1.35 |
0,8230 |
1,70 |
0,9109 |
2,25 |
0.9756 |
||||||||
Приложение 2. Таблица двоичных логарифмов целых чисел
|
1 |
0,00000 |
38 |
5,24793 |
75 |
6,22882 |
|
2 |
1 ,00000 |
39 |
5 ,28540 |
76 |
6,24793 |
|
3 |
1,58496 |
40 |
5,32193 |
77 |
6,26679 |
|
4 |
2,00000 |
41 |
5,35755 |
78 |
6,28540 |
|
5 |
2,32193 |
42 |
5,39232 |
79 |
6,30378 |
|
6 |
2,58496 |
43 |
5,42626 |
80 |
6,32193 |
|
7 |
2,80735 |
44 |
5,45943 |
81 |
6,33985 |
|
8 |
3,00000 |
45 |
5,49185 |
82 |
6,35755 |
|
9 |
3,16993 |
46 |
5,52356 |
83 |
6,37504 |
|
10 |
3,32193 |
47 |
5,55459 |
84 |
6,39232 |
|
11 |
3,45943 |
48 |
5,58496 |
85 |
6,40939 |
|
12 |
3,58496 |
49 |
5,61471 |
86 |
6,42626 |
|
13 |
3,70044 |
50 |
5,64386 |
87 |
6,44294 |
|
14 |
3,80735 |
51 |
5,67242 |
88 |
6,45943 |
|
15 |
3,90689 |
52 |
5,70044 |
89 |
6,47573 |
|
16 |
4,00000 |
53 |
5,72792 |
90 |
6,49185 |
|
17 |
4,08746 |
54 |
5,75489 |
91 |
6,50779 |
|
18 |
4,16993 |
55 |
5,78136 |
92 |
6,52356 |
|
19 |
4,24793 |
56 |
5,80735 |
93 |
6,53916 |
|
20 |
4,32193 |
57 |
5,83289 |
94 |
6,55459 |
|
21 |
4,39232 |
58 |
5,85798 |
95 |
6,56986 |
|
22 |
4,45943 |
59 |
5,88264 |
96 |
6,58496 |
|
23 |
4,52356 |
60 |
5,90689 |
97 |
6,59991 |
|
24 |
4,58496 |
61 |
5,93074 |
98 |
6,61471 |
|
25 |
4,64386 |
62 |
5,95420 |
99 |
6,62936 |
|
26 |
4,70044 |
63 |
5,97728 |
100 |
6,64386 |
|
27 |
4,75489 |
64 |
6,00000 |
200 |
7,644 |
|
28 |
4,80735 |
65 |
6,02237 |
300 |
8,229 |
|
29 |
4,85798 |
66 |
6,04439 |
400 |
8,614 |
|
30 |
4,90689 |
67 |
6,06609 |
500 |
8,966 |
|
31 |
4,95420 |
68 |
6,08746 |
600 |
9,229 |
|
32 |
5,00000 |
69 |
6,10852 |
700 |
9,451 |
|
33 |
5,04439 |
70 |
6,12928 |
800 |
9,644 |
|
34 |
5,08746 |
71 |
6,14975 |
900 |
9,814 |
|
35 |
5,12928 |
72 |
6,16992 |
1000 |
9,965 |
|
36 |
5,16993 |
73 |
6,18982 |
10000 |
13,288 |
|
37 |
5,20945 |
74 |
6,20945, |
Список литературы
1. Заездный А. М. Основы расчетов по статистической радиотехнике. М., «Связь», 1969.
2. Зюко А. Г. Помехоустойчивость и эффективность систем связи. М., «Связь», 1972.
3. Зюко А. Г. Элементы теории передачи информации. Киев, «Техника», 1969.
4. Котельников В. А. Теория потенциальной помехоустойчивости. М., Госэнергоиздат, 1956.
5. Кловский Д. Д. Передача дискретных сообщений по радиоканалам. М., «Связь», 1969.
6. Левин Б. Р. Теоретические основы статистической радиотехники. Книги первая и вторая. М., «Советское радио», 1968.
7. Петрович Н. Т. Передача дискретной информации в каналах с фазовой манипуляцией. М., «Советское радио» 1965.
8. Теплов Н. Л. Помехоустойчивость систем передачи дискретной информации. М., Связьиздат, 1964.
9. Тихонов В. И. Статистическая радиотехника. М., «Советское радио», 1966.
10. Фельдбаум А. А. и др. Теоретические основы связи и управления. М., Физматгиз, 1963.
11. Финк Л. М. Теория передачи дискретных сообщений. М., «Советское радио», 1970.
12. Xаркевич А. А. Борьба с помехами. М., Физматгиз, 1963.
13. Шеннон К. Работы по теории информации и кибернетике. Изд-во иностранной литературы, 1963.
14. Назаров М. В., Кувшинов Б. И., Попов О. В. Теория передачи сигналов. М.,«Связь», 1970.

