В основу построения системы XYZ были положены следующие условия.

1. Удельные координаты – кривые смешения не должны иметь отрицательных ординат, т.е. все реальные цвета определяются положительными значениями модулей основных цветов выбранной координатной системы и, следовательно, координаты цветности всех реальных цветов должны лежать внутри координатного треугольника основных цветов.
2. Количественная характеристика цвета – яркость – должна полностью определяться одним его компонентом.
3. Координаты белого цвета равноэнергетического излучения должны быть равными, т.е. точка цветности этого излучения должна лежать в центре тяжести треугольника основных цветов.

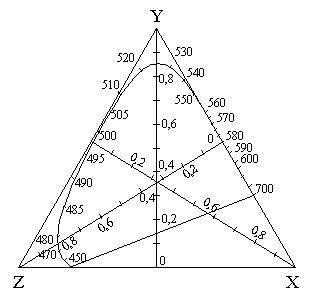
Для обеспечения первого требования в качестве основных цветов были выбраны три теоретических (реально не воспроизводимых) цвета XYZ. Координатная система XYZ выбрана так, чтобы векторы основных цветов находились в цветовом пространстве вне тела реальных цветов, т.е. тело реальных цветов находится внутри координатной системы XYZ, которая может быть пояснена с помощью рисунка 2.6. Оси X, Y, Z являются ортогональной декартовой системой координатных осей в цветовом пространстве – координата Y полностью определяется яркостью цвета, а два других основных цвета X и Z лежат в плоскости нулевой яркости. Вектор координаты перпендикулярен равноярким плоскостям, и в частности, плоскости нулевой яркости XOZ, что обеспечивает выполнение второго условия.

Любой цвет в системе XYZ описывается следующим выражением:

f'F = x'X + y'Y + z'Z,(2.15)

и изображается в цветовом пространстве точкой с координатами х', у', z' или вектором, проведенным в эту точку из начала координат. Модули основных цветов х', у', z' определяются выражениями, аналогичными (2.13):

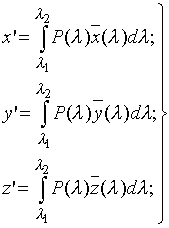(2.16)

Графики удельных координат (кривые смешения) в системе XYZ показаны на рисунке 2.7.

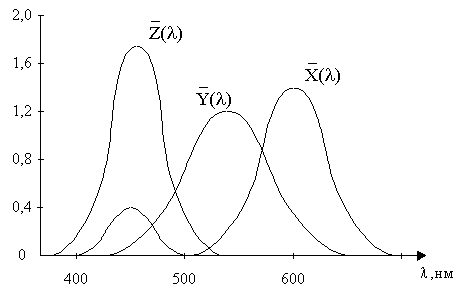
Рисунок 2.7. Удельные координаты цвета в системе XYZ

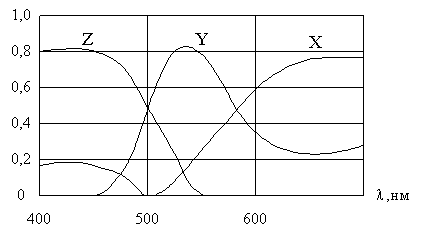
Рисунок 2.8. Координаты цветности в системе XYZ

Кривая у(λ) тождественна кривой стандартной относительной видности глаза V(λ). Две другие кривые х(λ) и z(λ) получены в результате пересчета удельных координат z'(λ), g(λ), b(λ) системы RGB в координатную систему XYZ. Подынтегральные площади всех трех кривых равны между собой, что обеспечивает выполнение третьего условия построения системы.

Цветовое пространство XYZ (рисунок 2.6) рассечено единичной плоскостью, определяемой уравнением

Х + Y + Z=1

и отсекающей на осях координат отрезки, равные Х=1, Y=1, Z=l. Линии пересечения координатных плоскостей с единичной плоскостью образуют на последней равносторонний треугольник. Точка m пересечения вектора D с единичной плоскостью характеризует направление этого вектора, а следовательно, и цветность описываемого цвета. Координаты точки m определяются выражениями

х = х'/М; у = у'/М; z = z'/M,

где М = х' + у' + z' – модуль цвета, а х, у, z – координаты цветности. Координаты цветности чистых спектральных цветов вычислены и стандартизованы МКО. Значения х, у, z для монохроматических излучений изображены графически на рисунке 2.8.

Геометрическое место координат цветности чистых спектральных цветов представляет собой кривую, лежащую на единичной плоскости и именуемую спектральным локусом (рисунок 2.6). Прямолинейный участок, замыкающий эту кривую в точках В и R, представляет цветности пурпурных цветов. Изображение цветностей на единичной плоскости или ее проекции называется диаграммой цветности – цветовым графиком. Таким образом, в единичной плоскости можно получить диаграмму цветности, показанную на рисунке 2.9, и представить на ней цветность любого цвета его координатами цветности.

Замкнутая коническая поверхность (рисунок 2.6), образуемая векторами чистых спектральных и пурпурных цветов, заключает в себе ту часть цветового пространства, где располагаются векторы всех реальных цветов, визуально воспринимаемых глазом. Все остальные векторы, расположенные за пределами этой конической поверхности, представляют формальные цвета, которые не могут быть визуально восприняты. Такими являются и сами первичные цвета XYZ МКО. Благодаря такому выбору первичных цветов цветовые компоненты всех реальных цветов в системе XYZ выражаются только положительными величинами. Соответственно на диаграмме цветности все точки, заключенные внутри спектрального локуса, представляют реальные цветности. Все точки вне спектрального локуса соответствуют формальным цветностям.

Так как одна из координат цветности является зависимой от двух других (x+y+z=l), то для определения цветности достаточно двух координат, например х и у. Тогда, проектируя диаграмму цветности единичной плоскости на плоскость ху в направлении оси z (рисунок 2.6), получим известную диаграмму цветности МКО (рисунок 2.10).

Рисунок 2.9. Диаграммы цветности в единичной плоскости XYZ

Рисунок 2.10. Диаграмма цветности МКО

Анализируя цветовой график МКО, необходимо отметить следующее.

1. Координаты цветности всех реальных цветов находятся внутри спектрального локуса и определяются положительными значениями х и у.
2. Равноэнергетический белый цвет Е находится в центре тяжести треугольника хоу. Его координаты цветности будут х=1/3, y=1/3.
3. Дополнительные цвета лежат на отрезке прямой, проходящей через точку Е с кривой спектральных цветов.
4. Цветность смеси двух цветов отображается точкой, лежащей на прямой, соединяющей смешиваемые цвета.
5. Цветность смеси трех цветов отображается точкой внутри треугольника, вершины которого образованы смешиваемыми цветами.

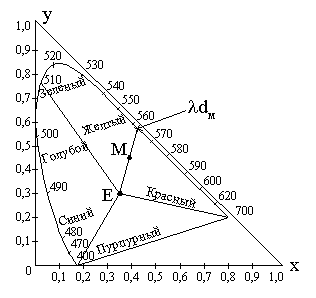
Выше указывалось, что цветность сложного излучения помимо координат цветности может быть охарактеризована цветовым тоном и насыщенностью. Цветовой тон любого цвета на диаграмме цветности МКО определяется длиной волны монохроматического излучения (доминирующей длиной волны λ_d), соответствующей пересечению кривой спектральных цветов – спектрального локуса с прямой, проходящей через точку Е и точку, отображающую цветность искомого цвета, например точку М. Насыщенность численно характеризуется чистотой цвета Р, т.е. относительным содержанием в нем спектрального цвета (монохроматического светового потока F_λ):

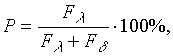
где F_δ – световой поток, вызывающий ощущение белого цвета. Насыщенность максимальна (Р = 100%) для чистых спектральных и пурпурных цветов и минимальна (Р = 0) для белого цвета