4.1. Электрические процессы в симметричных цепях
Электромагнитное поле симметричной цепи показано на рисунке. В отличие от коаксиального кабеля, не имеющего внешнего поля, в симметричной цепи поле открытое, действующее на значительном расстоянии.
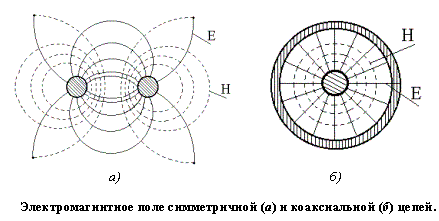
Под действием переменного поля происходит перераспределение электромагнитной энергии по сечению проводников, при этом наблюдаться следующие явления: поверхностный эффект; эффект близости соседних проводников; воздействие на параметры цепи окружающих металлических масс(соседних проводников, экрана брони). В симметричных кабельных цепях действуют все три фактора одновременно. В воздушных линиях, где провода расположены сравнительно далеко друг от друга и отсутствуют наружные металлические оболочки, следует учитывать лишь поверхностный эффект. В коаксиальных кабелях, являющихся закрытой системой, не учитывается действие окружающих металлических масс.
За счет указанных явлений происходит перераспределение электромагнитного поля и изменяются параметры цепей. Активное сопротивление R и емкость С возрастают, индуктивность L уменьшается. Наиболее существенно возрастет сопротивление цепи:
R = R0 + Rп.э + Rэ.б + Rм ,
где R0 - сопротивление постоянному току; Rп.э - сопротивление за счет эффекта близости; Rм- сопротивление, обусловленное потерями в окружающих металлических массах.
Поверхностный эффект был рассмотрен ранее.
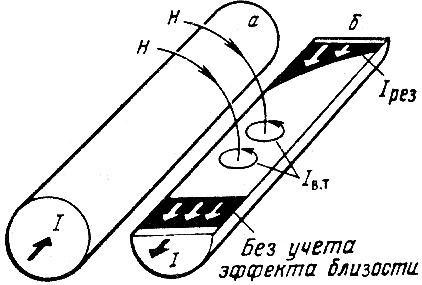
Эффект близости связан с взаимодействием внешних полей. Как видно из рис. 1, внешнее поле Н проводника а, пересекая толщу проводника б, наводит в нем вихревые тока. На поверхности проводника б, обращенной к проводнику а, они совпадают по направлению с протекающим по нему основным током (I+Iв.т), на противоположной поверхности проводника б, они направлены навстречу основному току (I- Iв.т). Аналогичное перераспределение токов происходит в проводнике а.
При взаимодействии вихревых токов с основным плотность результирующего тока на обращенных друг к другу поверхностях проводников а и б увеличиваться, а на отдаленных - уменьшается. Это явление ("сближение" токов в проводниках а и б) носит название эффект близости. Из-за неравномерного тока увеличивается активное сопротивление цепи переменному току.
Эффект близости также прямо пропорционален частоте, магнитной проницаемости, проводимости и диаметру проводника и, кроме того, зависит от расстояния между проводниками. С уменьшением этого расстояния действие эффекта близости возрастает в квадрате. Если по двум соседним проводникам токи проходят в одном направлении, то перераспределение их плотности из-за взаимодействия внешних электромагнитных полей приводит к увеличению плотности токов на взаимно отдаленных поверхностях проводников а и б.
4.2. Емкость и проводимость изоляции симметричной цепи
Емкость С и проводимость изоляции G связаны с процессами в диэлектрике. Под действием переменного электромагнитного поля в диэлектрике происходит смещение диполей, их переориентация и поляризация. Емкость характеризует способность поляризации и величину токов смещения, проводимость изоляции определяет величину потерь в диэлектрике на переориентацию диполей и характеризуется тангенсом угла потерь tgδ.
Емкость и проводимость изоляции симметричных цепей можно рассчитать по ранее выведенным формулам. Обычно принято проводимость изоляции выражать через тангенс угла диэлектрических потерь: tgδ=G/(ωC)=σ/(σεa). При этом G= ωπεatgδ/ln[(a-r/r)]=ωC tgδ. Заменяя в данном выражении εa=εоεr, где εо =10 - 9 /(36π), получим для 1 км кабеля, Ф/км,
(1.1)
Соответственно G= ωΡtgδ, См/км, где εrи tgδ - диэлектрическая проницаемость и тангенс угла диэлектрических потерь; а - расстояние между проводниками; r - радиус проводника.
Реальные конструкции симметричных кабелей, как правило, содержат много пар и находятся в общих металлических оболочках. С учетом близости соседних пар и влияния наружной металлической оболочки емкость симметричных кабелей для различных типов скрутки рассчитывают по следующей формуле, Ф/км:
С=
εr 10 - 6 / [36 ln(aψ/r)], (1.2)
где - коэффициент скрутки кабельных цепей (1,02 … 1,07); εr- эффективная диэлектрическая проницаемость изоляции; ψ - поправочный коэффициент, характеризующий близость металлической оболочки проводников.
Расчетные формулы коэффициента ψ для различных видов группообразования кабелей приведены ниже:
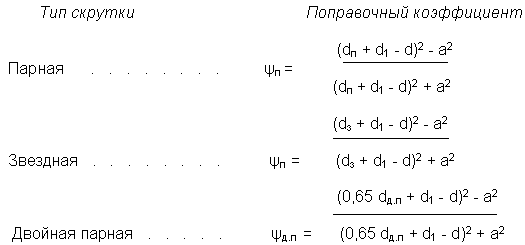
При расчете проводимости изоляции G следует, кроме проводимости, обусловленной диэлектрическими потерями, учитывать также проводимость, обусловленную утечкой тока в силу несовершенства диэлектрика: G0=1/Rиз ..
По величине эта проводимость изоляции обратно пропорциональна сопротивлению изоляции кабеля (линии). В результате проводимость изоляции кабельной цепи, См/м,
G=G0+Gf=1/Rиз.=ωΡtgδ. (1.3)
При расчете проводимости изоляции кабельных линий учитывают, что по абсолютной величине потери в диэлектрике при переменном Gf существенно больше, чем при постоянном токе G0, по этому проводимость в кабельных линиях рассчитывают по формуле G=Gf.=ωΡtgδ. При рассчете проводимости изоляции по постоянному току G0 принимают: для городских телефонных кабелей Rи= 2 000 МОм·км, а для кабелей дальней связи - 10 000 МОм·км.
Кабели связи, как правило, имеют сложную комбинированную изоляцию, состоящую из твердого диэлектрика (бумаги, стирофлекса, полиэтилена и др.) и воздуха. Результирующие эквивалентные значения диэлектрической проницаемости εэ.и угла диэлектрических потерь tgδэ сложной изоляции определяются электрическими свойствами и соотношением объемов составных ее частей. Причем эквивалентные значения εэ.и tgδэ сложной изоляции близки к величинам ε и tgδ той части изоляции, которая занимает большой объем.
Рассмотрим графики зависимости первичных параметров линий связи R, L, C, G от частоты, диаметра проводника и расстояния между проводниками.
С увеличением частоты значение параметров R и G возрастает за счет потерь в проводниках на вихревые токи и в изоляции на диэлектрическую поляризацию, а индуктивность L уменьшается,так как из-за поверхностного эффекта уменьшается внутренняя индуктивность проводника. Емкость C от частоты не зависит.
При увеличении расстояния между проводниками параметры R, C, G закономерно уменьшаются, а индуктивность L возрастает. Снижение R обусловлено уменьшением потерь на эффект близости. Рост L связан с увеличением площади контура, пронизываемого магнитным потоком. Емкость C уменьшается, так как проводники удаляются друг от друга и уменьшается их взаимодействие.
С увеличением диаметра проводников параметры C и G растут, а L уменьшается. Изменение активного сопротивления имеет сложный характер. Это обусловлено тем, что с увеличением диаметра проводника сопротивление постоянному току резко уменьшается, а сопротивление за счет поверхностного эффекта и эффекта близости растет. Поэтому вначале R снижается резко, а затем снижение замедляется.
Порядок величин первичных параметров существующих типов линий связи следующий: R=5 . . . 200Ом/км; L=0,6 … 2 мГн/км; С=5… 50 мФ/км; G=1 … 200 мкСм/км. В кабельных линиях за счет тонких проводников и близкого их расположения превалируют параметры R и C. Емкость кабеля в 3…5 раз больше емкости воздушной линии, а активное сопротивление - в 5…10 раз. Индуктивность кабеля, наоборот, меньше в 2…3 раза.
Теоретически от температуры зависят все четыре первичных параметра. Однако практически следует учитывать лишь температурную зависимость активного сопротивления. Изменение от температуры L, C, G весьма незначительно.
Температурная зависимость активного сопротивления цепи определяется по формуле
Rt=R20[1+αR(t-20)], (2.1)
где Rt - сопротивление при температуре t˚ C; R20- тоже при температуре 20˚С;
αR - температурный коэффициент сопротивления, равный для меди 0,004 и для алюминия 0,0037.
С увеличением сопротивление цепи растет. Физически это объясняется тем, что с увеличением температуры возрастает хаотическое движение атомов решетки и затрудняется прохождение электронов через нее.
Вторичные параметры симметричных цепей Zв, α, β, υ рассчитываются по формулам, приведенным ранее в таблице. В ряде случаев вторичные параметры выражают непосредственно через параметры цепей (a,d) и качество исходных материалов (ε, tgα).
Подставив в формулу Zв =√L/C значения L и C получим значение волнового сопротивления симметричной цепи, Ом,
Коэффициент затухания симметричной цепи с медными проводниками, дБ/км,
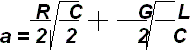
Путем подстановки в эту формулу значений первичных параметров:
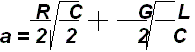(2.2)
Коэффициент фазы, рад/км, определяется формулой
β=ω√LC или β=ω√ε/c , (2.3)
где с- скорость света , равна 30 000 км/с.
Скорость распространения энергии, км/с,
υ=1√LC=с/√ε. (2.4)
Типовые частотные зависимости вторичных параметров цепи распространяются и на симметричные цепи.
