1. Общие сведения и структура радиосистемы передачи информации
1.1. История развития радиосистем передачи информации
1.3. Технические требования к космическим РСПИ
2. Особенности представления информации
2.1. Формы представления информации
2.2. Классификация дискретных представлений
3. Дискретно-аналоговое представление
3.1. Дискретно-аналоговое представление регулярными выборками
3.2. Физическая трактовка процессов интерполяции сигналов
3.3. Задачи идеальной интерполяции
4. Обобщенные дискретные представления
5. Сжатие данных при телеизмерениях
5.2. Классификация и основные характеристики метода сжатия данных
5.4.1. Алгоритмы полиноминальных методов сжатия
5.4.2. Экстраполяционные методы сжатия
5.4.3. Оптимальное линейное предсказание
6. Структурная схема адаптивной системы сжатия данных
6.2. РТМС с адаптивной дискретизацией
6.2.1. РТМС со сжатием данных по полосе
6.2.2. РТМС с адаптивной дискретизацией в каждом канале с буферной памятью
6.2.3. РТМС с исключением избыточных данных
6.3. РТМС с адаптивной коммутацией каналов
6.3.1. Обобщенная структурная схема
6.3.2. РТМС с адаптивной коммутацией каналов при параллельном анализе погрешности
6.4. РТМС с автоматическим регулированием частоты опроса датчиков
7. Методы рационального кодирования
7.2. Равномерное квантование мгновенных значений сигнала
7.3. Неравномерное квантование мгновенных значений
7.6. Теория разностного кодирования
7.8. Адаптивно-разностная ИКМ (АРИКМ)
8. Разделение каналов в радиолинии
8.2. Классификация методов разделения каналов
8.3. Условия линейной разделимости сигналов
8.4. Разделение сигнала по форме
8.5. Частотное разделение каналов (ЧРК)
9. Радиотелеметрические системы с временным разделением каналов
9.1. Виды модуляции, применяемые в системах с ВРК
9.1.1. Амплитудно – импульсная модуляция (АИМ)
9.2. Переходные искажения в системах ВРК
9.3. Помехоустойчивость РТМС с ВРК
9.4. Многоступенчатая коммутация в РТМС с ВРК
9.5. Синхронизация в РТМС с ВРК
10.1. Общие сведения о цифровых РТМС
10.2. Функциональная схема цифровой РТМС
11. Радиотелеметрическая система с ЧРК
11.1. Виды модуляции, применяемые в системах с ЧРК
11.1.1. Линейная амплитудная модуляция
11.2. Характеристики группового тракта
11.3. Причины появления искажений в ТМ системах с ЧРК
11.3.2. Переходные искажения (линейные)
11.3.3. Перекрестные искажения (нелинейные)
11.3.3.1. Перекрестные искажения в низкочастотной части группового тракта
11.3.3.2. Перекрестные искажения в высокочастотной части группового тракта
1. Общие сведения и структура радиосистемы передачи информации
1.1. История развития радиосистем передачи информации
Наибольшее развитие радиосистем передачи информации (РСПИ) связано с разработкой системы многоканальной связи и радиотелеметрических систем (РТМС). Более подробно рассмотрим особенности таких РСПИ как РТМС.
Термин «телеметрия» в переводе с греческого означает дальние измерения. Телеметрическая информация дает возможность контролировать состояние удаленного объекта и управлять им на расстоянии. Таким образом РТМС обеспечивают сбор, обработку, передачу по радиолинии измеренной информации о состоянии или поведении технических устройств, живых организмов и других объектов, удаленных от потребителя этой информации.
Измеряемая информация – это информация, результаты измерения которой могут быть выражены в единицах измерения физических величин.
РТМС широко применяют в промышленности, медицине, биологии, при исследовании океанских и земных глубин, космоса. Научные основы РТМС заложены в результате развития теории информации, многоканальной связи и математических методов обработки информации, в частности систем сжатия данных.
Практическое использование РТМС стало возможным благодаря достижениям в области микроминиатюризации элементов РСПИ и разработки микропроцессоров, микроконтроллеров, ПЛИС и т.д. Успехи в области теории передачи информации связаны с именем таких отечественных ученых, как В.А.Котельников, В.И.Сифоров, А.П.Мановцев, В.Ю.Типугин, П.А.Агаджанов и др.[1].
История развития радиотелеметрии начинается с 1930 года, когда с шара – зонда, выполненного под руководством профессора П.А.Молчанова, были переданы такие метеорологические данные, как давление, температура, влажность. В конце 30-х годов под руководством академика С.Н.Вернова был разработан радиозонд, предназначенный для изучения космических радиаций. С 40-х годов РТМС стали использоваться при испытаниях самолетов, управляемых снарядов, искусственных спутников Земли и космических кораблей. В настоящее время РТМС используются в газовой, топливной и химической промышленности, а также металлургии и ядерных установках.
1.2. Задачи космических РСПИ
К основным задачам космических РСПИ относятся [1]:
- Сбор измерительной информации от разных источников на борту космического аппарата, а также сжатие и преобразование в форму, удобную для передачи в радиолинию.
- Передача телеметрической информации с борта космического аппарата по радиолинии и прием на Земле.
- Обработка принятой телеметрической информации, регистрация и представление в форме, удобной для потребителя.
Первоначально главной задачей в радиотелеметрии была передача сообщений и теория телеметрии сводилась к теории многоканальной радиосвязи. В настоящее время основными задачами являются первая и третья задачи.
Это вызвано следующими причинами:
- РТМС стали использоваться для обслуживания сложных объектов;
- увеличилось число источников измерения информации;
- увеличился объем передаваемой информации;
- увеличилась дальность связи;
- появились жесткие ограничения на вес и габариты бортовой аппаратуры.
Круг задач, решаемый современными РТМС, значительно шире, чем у систем многоканальной связи и включают в себя следующие требования:
- Предание РТМС свойств адаптации к текущей обстановке (например, путем регулировки частоты опроса).
- Рациональное формирование сообщений на борту объектов (например, путем разработки эффективных систем кодирования).
- Устранение избыточности, т.е. сжатие объемов сообщений (например, применяя адаптивную коммутацию и дискретизацию).
- Автоматизация процессов обработки информации на Земле.
- Получение некоторой части информации незамедлительно.
Реализация этих требований привела к тому, что РТМС должны рассматриваться как пространственно – разнесенные информационные радиосистемы, включающие в себя ряд разнородных, но связанных между собой систем.
1.3. Технические требования к космическим РСПИ
1. Одновременное измерение и передача информации о многих параметрах.
2. Обеспечение высокой точности измерений. По точности РТМС делятся на 3 класса: средней точности (погрешность 3 – 5%), высокой точности (1 – 2%), очень высокой точности (0.1 – 0.5%). Очень высокую точность обеспечивают только цифровые РТМС.
3. Обеспечение передачи сообщений с различной шириной спектра (от единиц Гц до сотен кГц).
4. Бортовая аппаратура должна быть максимально проста, надежна, иметь малые массу, габариты, потребление энергии.
5. Наземная аппаратура должна автоматически обрабатывать информацию, поступающую на Землю с различной скоростью передачи.
1.4. Основные подсистемы космических РСПИ
Космические РСПИ относятся к большим системам. Выделяют три основные подсистемы (рисунок 1.1):
- бортовая информационная подсистема;
- радиолиния;
- наземная информационная подсистема.
Рисунок 1.1
Сигналы, снимаемые с выхода первичного преобразователя ( ПП ) и подаваемые на вход РТМС – называются первичными. ПП осуществляет преобразование неэлектрической величины в электрическую. Кроме первичных сигналов в космические РТМС передаются дополнительные сигналы, необходимые для масштабирования, синхронизации и других задач. ПП обычно состоит из датчика и согласующего устройства (рисунок 1.2),
Рисунок 1.2
где 
- первичный процесс, являющийся неэлектрической величиной, 
- электрическая величина.
Датчик осуществляет основные преобразования реализации измеренного параметра в электрический сигнал . Согласующее устройство преобразует электрический сигнал к виду, на который рассчитаны входные цепи РТМС.
По виду измеряемых параметров датчики подразделяют на датчики обеспечивающие:
- контроль процессов путем:
- непосредственного преобразования;
- модуляции параметров;
- контроль событий:
- сигнальные;
- счетные.
В случае контроля процессов на вход ПП поступает процесс , а при контроле событий входная величина является дискретной ( например, удар метеорита).
Датчик непосредственного преобразования процессов обеспечивает преобразование в непосредственно в соответствии с функцией 
. У модуляционных датчиков процесс используется для модуляции одного из параметров гармонического или импульсного сигнала .
Сигнальные датчики фиксируют факт наступления определенного события. Каждому событию соответствует определенный сигнал, который передается на наземную подсистему.
Счетные датчики обеспечивают подсчет и передачу числа однородных событий, например, число ударов метеорита.
В бортовых информационных системах осуществляется сжатие и уплотнение канала передачи, т.е. сообщение представляется в форме, обеспечивающей устранение избыточности. При этом выбрасываются избыточные отсчеты и передаются только представляющие интерес параметры.
Основной особенностью радиолинии является её многоканальность, составляющая от 10 до 105 каналов. К радиолинии предъявляются требования по обеспечению заданной дальности, надежности, скрытности и помехоустойчивости связи.
В наземных информационных подсистемах осуществляется предварительная обработка результатов измерений, т.е. устраняются грубые ошибки, проверяются условия стационарности, производится оценка параметров. Наземная информационная подсистема выдаёт результаты измерений в удобном для получателя виде. Получателем информации может быть ЭВМ, человек, техническое устройство.
1.5. Упрощенная структурная схема космической РСПИ
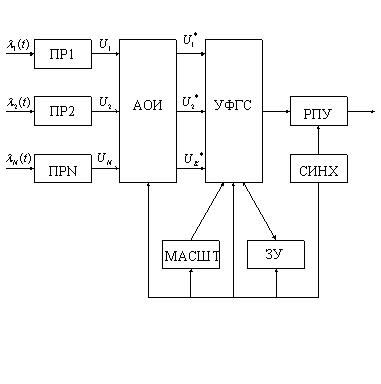
Рисунок 1.3
Структурная схема передающей части космической РСПИ имеет вид изображенный на рисунке 1.3.
В состав этой структурной схемы передающей части космической РСПИ входят первичные преобразователи (ПР), аппаратура обработки информации (АОИ), устройство формирования группового сигнала (УФГС), радиопередающие устройства (РПУ), устройство масштабирования, запоминающее устройство (ЗУ) и синхронизатор.
Сигналы U1 , U2 , … ,UN c выхода ПР поступает на вход АОИ. На вход АОИ могут поступать сигналы непосредственно с контролирующих приборов и систем, если подлежащие измерению параметры являются элементарными.
АОИ решает следующие задачи [2]:
1. Сокращение избыточности передаваемой информации.
2. Управление сбором информации на объекте в зависимости от меняющейся ситуации.
3. Согласование производительности бортовых измерительных систем с пропускной способностью радиоканала.
Рисунок 1.4
Структура УФГС зависит от метода разделения каналов. В общем случае УФГС можно изобразить в следующем виде (рисунок 1.4):
Сигналы с генератора канальных сигналов (ГСК) поступают на канальные модуляторы (КМ). В системах с частотным разделением каналов (ЧРК) эти сигналы представляют собой синусоидальные колебания с различными поднесущими частотами (рисунок 1.5), а в системе с временным разделением каналов (ВРК) это последовательность импульсов, разнесенных по времени (рисунок 1.6).
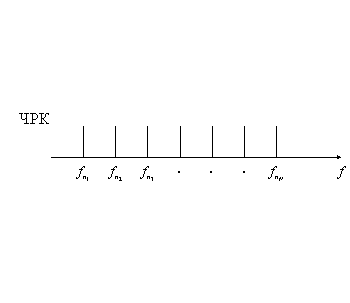
Рисунок 1.5
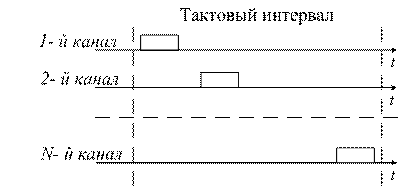
Рисунок 1.6
В системе с разделением каналов по форме канальные сигналы совпадают по времени и частоте, но различаются по форме.
Для синхронизации различных устройств, входящих в состав РТМС, используется синхронизатор. ЗУ используется на летательных аппаратах и низкоорбитальных космических аппаратах. В начале осуществляется накопление информации в ЗУ на участках полета, где отсутствует связь между контролируемым объектом и наземным приемником станции. После восстановления связи с наземными приемными станциями накопленные данные передаются.
В телеметрии важное значение имеет абсолютная величина измеряемых физических параметров с привязкой по времени, т.е. телеметрическая информация должна быть масштабирована. Масштабирование осуществляется по уровню и по времени. Для масштабирования по уровню потребитель должен знать амплитудную характеристику датчика 
, а также калибровочную характеристику информационного канала РТМС 
. Эта характеристика может сниматься заранее, но из-за нестабильности параметров измеряемой системы приходится периодически передавать известные значения эталонных уровней сигнала. Обычно калибровка производится с периодом 10 -15 секунд путем передачи на вход информационных каналов сигналов, соответствующих 0%, 50%, 100% напряжения питания датчиков.
Масштабирование по времени осуществляется путем формирования сигнала времени в пункте приема или передачи этих сигналов вместе с данными телеизмерений.
Структурная схема приемно-регистрирующей аппаратуры изображена на рисунке 1.7, где РУ – регистрирующее устройство:
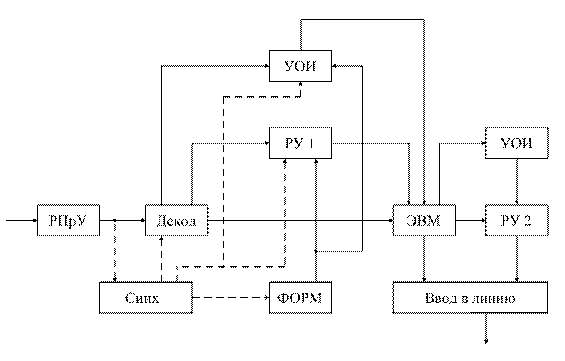
Рисунок 1.7
Сигналы с выхода радиоприемного устройства (РПрУ) поступают на вход устройства декодирования (Декод) и также на синхронизатор (Синх) и далее на формирователь (ФОРМ) сигналов в системе синхронизации с ВРК. В системе ЧРК синхронизатор отсутствует.
Обычно весь групповой сигнал после преобразования записывается в регистрирующее устройство РУ1 в цифровой форме. Зарегистрированная информация повергается обработке, которой предшествует отбор результатов регистрации и исключение ненужных данных (экспресс-анализ) с помощью устройства отображения информации (УОИ).
В результате обработки информации в ЭВМ поступают таблицы или графики измерения телеметрических параметров в истинном масштабе времени.
Кроме этого производится отбраковка ложных измерений, выделение экстремальных значений параметров и др. Результаты обработки представляются на визуальных индикаторах и записываются в РУ2, а также представляются в удобном виде для передачи в линии связи.
2. Особенности представления информации
2.1. Формы представления информации
Наиболее характерными для современных РСПИ являются три формы представления сообщений, которые формируются на борту и передаются по линиям связи:
1. Сообщения о наличии/отсутствии некоторого априорно известного сообщения (включения/выключения двигателей, удары метеорита). В этом случае требуется определить момент времени, когда произошло событие. Параметры указанного типа называются сигнальными. Для фиксации события имеется несколько возможностей:
а) в момент совершения события посылается специальный сигнал;
б) в момент совершения события изменяется уровень напряжения, который подлежит измерению.
2. Сообщения о величинах характеризуют значения параметров в определенный момент времени. Контролируемые величины имеют различную физическую природу. Поэтому, для формирования сообщений используются первичные преобразователи. При нелинейности канала передачи необходимо произвести калибровку амплитуды и масштабирование по времени.
3. Сообщения о процессах должны с заданной точностью воспроизводить процессы на определенном отрезке времени, т.е. в этом случае также необходимо производить калибровку амплитуды и масштабирование по времени.
Существует два основных способа представления процессов: аналоговый и дискретный. Аналоговое представление заключается в том, что электрическая величина, играющая роль сообщения, формируется непрерывно. Такое представление используется в системах ЧРК, где непрерывное напряжение модулирует несущие или поднесущие гармонические колебания. Дискретное представление делится на дискретно-аналоговое и дискретно-квантованное (цифровое). Дискретно-аналоговое представление сводится к тому, что непрерывный процесс 
заменяется совокупностью аналоговых выборок, которые формируются через определенные интервалы времени (используются АИМ, ШИМ, ВИМ). Дискретно-квантованное представление отличается от дискретно-аналогового тем, что выборки формируются в цифровой форме.
2.2. Классификация дискретных представлений
Дискретно-аналоговые и цифровые представления могут быть классифицированы следующим образом (рисунок 2.1).
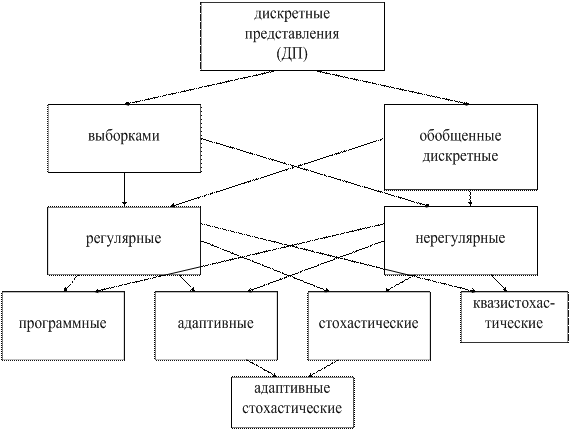
Рисунок 2.1
Дискретные представления – это процесс замены непрерывного сообщения x(t) (первичный сигнал) функцией дискретного времени 
. В общем случае дискретное представление может быть описано выражением:
Х1,Х2,…,Хn = АХ(t), (2.1)
где Х1…Хn – координаты сообщения; А – оператор представления.
При линейности оператора представления справедливо равенство:
, i = 1,2,...n , (2.2)
где Vi(t) – весовая функция ; Т – интервал представления.
Исходное сообщение восстанавливается с помощью оператора восстановления В по формуле:
, (2.3)
где Wi(t) – координатная (восстанавливающая, синтезирующая) функция, знак * указывает отличие восстановленного сообщения от исходного за счет искажений и шумов.
При представлении выборками весовые функции Vi(t)= δ(t – ti) , при этом Xi =X(ti).
При обобщенном дискретном представлении координаты сообщения представляют собой коэффициенты некоторого ряда, это позволяет сократить количество координат, т.е. объем выборки. В качестве координат функций могут использоваться полиномы Чебышева, Лежандра, Уолша и др.
При регулярных дискретных представлениях координаты X1, Xn формируются через одинаковые промежутки времени. Такие системы наиболее широко распространены благодаря простоте технической реализации.
Определим основные особенности классов дискретных представлений.
Программируемые дискретные представления предусматривают возможность изменения алгоритма представления, объема координат, показателя точности и других характеристик по определенной априори установленной программе.
Адаптивные дискретные представления дают возможность изменять те же характеристики автоматически на основе анализа данных об изменяемом сообщении и имеют цель приспособиться к этим изменениям.
Приведем классификацию адаптивных алгоритмов дискретизации (рисунок 2.2).
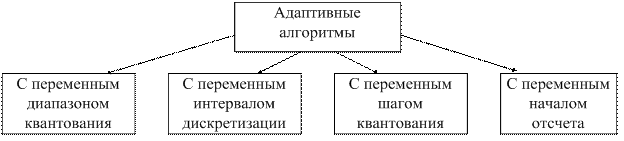
Рисунок 2.2
Адаптивные дискретные представления с переменным диапазоном квантования позволяют уменьшить объем сообщения при заданном показателе верности путем согласования динамического диапазона характеристики квантования и диапазона сигнала (например система адаптивной импульсно – кодовой модуляции).
Система с переменным интервалом дискретизации (например, система адаптивной дискретизации) используется, когда в процессе передачи изменяется полоса спектра частоты сообщения. Введение такой адаптации позволяет в несколько раз уменьшить среднюю частоту дискретизации.
Система с переменным шагом квантования (например, система адаптивной δ – модуляцией) позволяет уменьшить, по сравнению с равномерным квантованием, среднеквадратическую погрешность представления или уменьшить требуемую скорость передачи.
Система с переменным уровнем начала отсчета обычно использует разностные виды модуляции, например разностную импульсно – кодовую модуляцию. Формирование разностей значений выборок равноценно перемещению уровня начала отсчетов, что позволяет уменьшить число уровней квантования.
Стохастические дискретные 
представления предполагают преднамеренное введение элемента случайности в процесс преобразования сообщения для увеличения точности представления исходного процесса. В псевдослучайный шум добавляют сигнал перед квантованием, а на приемной стороне осуществляется подсчет квантованных значений двух соседних уровней в интересах увеличения точности представления.
При квазистохастических ДП используется комбинация детерминированного и случайного элемента в процессе формирования координат сообщения.
Адаптивные стохастические представления – результат соединения адаптивных и стохастических представлений, при которых одна группа характеристик изменяется стохастически, а другая адаптируется к измененному сообщению.
2.3. Рациональное представление информации
При ракетно–космических исследованиях наметилась постоянная тенденция к росту космических измерений и регистрации на борту летательного объекта информации. На ракете – носителе Сатурн – 5 системой измерения контролировалось около 2400 сигналов, а объем измерений в одном пуске достигал 6 млрд. двоичных слов. Для космического аппарата «Аполлон» этот объем возрос на порядок при количестве датчиков равном 20 тыс. Для космического объекта типа «Пионер – 10», предназначенного для проведения измерений в дальнем космосе, объем измерений равен 
двоичных слов. Эти обстоятельства обусловливают необходимость увеличения скорости передачи информации по радиоканалам.
Стоимость радиоканала передачи информации в настоящее время соизмерима, а иногда превышает стоимость бортовой системы. Однако по оценкам специалистов в связи со сложностью алгоритма вторичной обработки информации при анализе характеристик летательного и космического аппарата обычно используют 5-10% данных, полученных с борта. Для вычисления вероятностных характеристик наблюдаемых параметров бывает достаточно обработать 0,1-1% полученной информации. Т.о, эффективность бортовой системы измерений низка, несмотря на затраты значительных средств. В связи с этим системы телеизмерений на борту стали превращаться в бортовые системы сбора и обработки информации (БССО). Одна из первых систем БССО была разработана для ракет типа ТИТАН -3.
Эта БССО выполняла следующие задачи:
- Адаптивный опрос и сжатие телеметрической информации.
- Вычисление статистических характеристик наблюдаемых процессов.
- Кодирование информации с контролем достоверности.
- Определение летно-тактических характеристик бортовой системы.
Благодаря использованию ЭВМ стало возможно перенести на борт целиком или частично обработку измеряемых данных. Только таким путем, а не увеличивая пропускную способность канала передаваемой информации, можно решить задачу передачи возрастающего объема сведений. Дальнейший рост скорости передачи информации в УКВ и СВЧ диапазонах затруднен. Поэтому, начиная с 1965 года, начинают интенсивно изучаться различные методы рационального представления информации.
Основные направления исследований:
- Согласование частот опросов с характеристиками сигнала в случае регулярных выборок и заданном способе восстановления сообщения.
- Разработка эффективных обобщенно-дискретных представлений сообщений.
- Разработка квазиобратимых методов сжатия данных.
- Исследование методов эффективного кодирования.
- Определение помехоустойчивых кодов и узкополосных методов модуляции.
Натурные испытания алгоритмов квазиобратного сжатия данных на ракете “Полярис” показали, что при точности восстановления данных 1% средний коэффициент сжатия составляет 12-30. Использование системы сжатия данных на космическом аппарате “Апполон” сократило затраты на 200 млн. $. Наибольшего эффекта в смысле сокращения избыточности следует ожидать от реализации методов необратимого сжатия, которые не позволяют восстановить на приемной стороне передаваемую реализацию как функцию времени.
2.4. Точностные характеристики передаваемой информации
Для характеристики точности передаваемой информации в РТМС применяют различные показатели верности. В соответствии с введенной выше классификацией необходимо получить оценки точности величины, функции и совокупность величин.
1. Величина 
(рисунок 2.3), где 
- текущая ошибка.
Рисунок 2.3
В качестве показателя верности используется: 1. Среднеквадратическое отклонение (СКО)
, (2.4)
где 
- операция усреднения, 
- среднее значение ошибки. 2. Среднеквадратическое значение (СКЗ)
. (2.5)
3. Относительная ошибка 
, где 
.
В ряде случаев бывает удобно приводить ошибки не к шкале 
, а к эффективному значению сигнала. Для эргодических процессов СКЗ сигнала совпадает с эффективным значением.
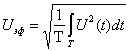. (2.6)
Тогда эффективная относительная ошибка равна: 
.
Обычно в РСПИ используется понятие отношения сигнал/шум, связанное с эффективной относительной ошибкой соотношением: 
.
2. Функция 
(рисунок 2.4), где 
- текущая ошибка.
Рисунок 2.4
В качестве показателей верности используются математически вводимые расстояния:
, (2.7)
. (2.8)
3. Совокупность величин (рисунок 2.5), где 
, 
, … , 
- текущая ошибка.
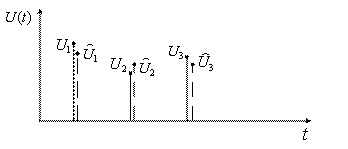
Рисунок 2.5
При оценке совокупности величин в качестве показателя вероятности используют:
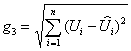(2.9)
(2.10)
3. Дискретно-аналоговое представление
3.1. Дискретно-аналоговое представление регулярными выборками
При дискретно-аналоговом представлении сообщение на интервале времени T описывается вектором 
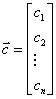, (3.1)
где 
- координаты.
Если шкала каждой координаты непрерывная, то это представление называется дискретно-аналоговым, а если шкала квантованная, то представление дискретно-квантованное, т.е. цифровое.
Дискретно-аналоговое представление сообщений может быть реализовано различными способами в зависимости от выбора системы координат. Наибольшее применение в РСПИ получили представления, у которых в качестве координат 
сообщения используется текущее значение сигнала в фиксированные моменты времени.
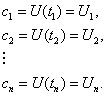(3.2)
Координаты 
называются выборками или отсчетами, а моменты времени 
- точками опроса.
При представлении регулярными выборками расстояние между соседними точками опроса одинаково и равно 
.
, (3.3)
где - период опроса, 
- частота опроса.
Частота опроса является важнейшим параметром, который надо выбирать при представлении сообщения регулярными выборками.
Процесс формирования выборок в этом случае изображен на рисунке 3.1:
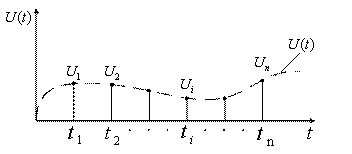
Рисунок 3.1
Выбор частоты опроса 
зависит от способа восстановления исходного сообщения на приемном конце. Восстановление непрерывной функции по её выборкам называется интерполяцией.
Рассмотрим случай, когда потребителю необходимо восстановить на приёмной стороне функцию. Реально при восстановлении функции может быть получена только её оценка 
. Для доказательства этого утверждения представим интерполяционную обработку в следующем виде:
, (3.4)
где 
- интерполирующая (восстанавливающая, синтезирующая) функция. Функция
, (3.5)
т.е. есть функция с началом отсчета в точке мер выборки первичного сигнала. Суммирование в выражении (3.4) ведется по всем выборкам, участвующим в обработке. Определение вида функции составляет сущность задачи выбора способа интерполяционной обработки.
На точность функции восстановления функции влияют следующие факторы:
- шумы интерполяции;
- шумы радиолинии;
- погрешности системы.
В дальнейшем будем учитывать только ошибку за счет интерполяции. Т.е. выборки будут считаться точными, а шумы отсутствующими. Тогда выражение для оценки первичного сигнала будет иметь следующий вид:
. (3.6)
Ошибка интерполяционной обработки в этом случае равна:
. (3.7)
При этом оценка должна быть получена на некотором интервале интерполяции 
с учетом выборок, расположенных на конечном интервале обработки 
. Интервал обработки должен последовательно перемещаться в пределах интервала наблюдения 
(рисунок 3.2).
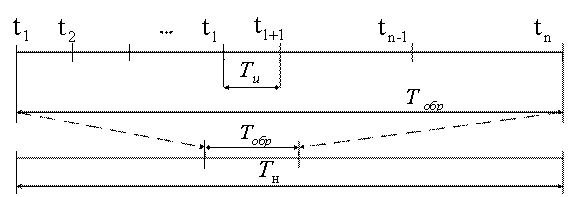
Рисунок 3.2
Таким образом, функция должна быть восстановлена для всех значений времени, лежащих внутри интервала интерполяции , путем использования выборок в моменты времени 
.Это возможно потому, что существует корреляционная зависимость между значением первичного сигнала , моментами времени 
и 
. Интерполяция белого шума невозможна, т.к. его корреляционная функция есть дельта – функция.
Теоретически необходимо учитывать все отсчеты 
на интервале наблюдения , т.е. полагать = . Но при этом результаты интерполяции могут быть получены спустя время , и для реализации требуется устройство с большой памятью. С удалением точки опроса от интервала интерполяции уменьшаются корреляционные связи и их учет дает малый вклад в ошибку интерполяции. Поэтому имеют смысл учитывать только те отсчеты, выборки которых коррелированны с функцией на интервале интерполяции , с коэффициентами корреляции К(τ) = 0.05 – 0.2. Конкретные значения К(τ) определяются требованиями к точности интерполяции.
3.2. Физическая трактовка процессов интерполяции сигналов
Основное математическое соотношение интерполяционной обработки:
, (3.8)
можно проиллюстрировать следующим образом (рисунок 3.3).
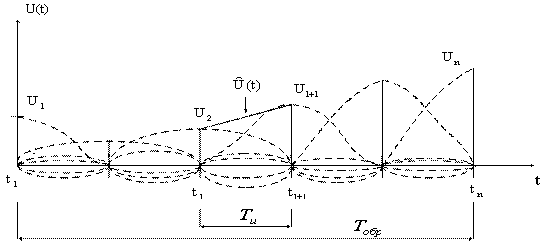
Рисунок 3.3
В качестве интерполяционной функции в этом примере используется функция 
. Интервалы интерполяции и обработки должны последовательно сдвигаться по времени. Операцию интерполяции можно выполнить с помощью линейного фильтра с импульсной характеристикой вида:
. (3.9)
Для доказательства этого утверждения обозначим сигнал на входе и выходе линейного фильтра через 
и 
(рисунок 3.4):
Рисунок 3.4
Представим сигнал на входе линейного фильтра в виде последовательности кратковременных импульсов, площадь которых равна соответствующим выборкам
. (3.10)
Из свойств линейных систем следует, что сигнал на выходе равен:
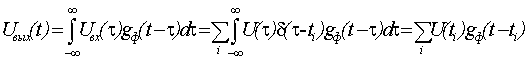(3.11)
Выражение (3.11) получается с учетом фильтрующего свойства δ-функции. Если импульсная характеристика линейного фильтра 
удовлетворяет выражению (3.9), то соотношение (3.11) переходит в формулу для интерполяционной обработки:
. (3.12)
Идеальное восстановление функции на выходе линейного фильтра невозможно, т.к.:
- отклик на выходе линейного фильтра не может появиться раньше соответствующей выборки на входе;
- число выборок не равно бесконечности;
- АЧХ фильтра отличается от идеальной.
3.3. Задачи идеальной интерполяции
В общем случае формула интерполяции имеет вид:
, (3.13)
- оценка значения i-ой выборки, - восстановленный первичный сигнал, 
.
Интерполяция возможна в том случае, если в сигнале имеются корреляционные связи. Может быть поставлена задача оптимального выбора вида функции 
, при которой ошибка интерполяции минимальна.
Рассмотрим задачу идеальной интерполяции сигнала при предположении, что 
, т.е. отсутствуют внешние шумы и ошибки системы.
Пусть непрерывный первичный сигнал описывается корреляционной
функцией 
. Требуется определить форму интерполирующей функции, обеспечивающей при заданных значениях коэффициента корреляции минимум СКО
. (3.14)
Можно показать, что в этом случае оптимальная интерполирующая функция имеет вид:
, (3.15)
где 
- весовые коэффициенты, однозначно связанные со значениями коэффициентов корреляции в точках 
, 
.
Т.о., оптимальная интерполирующая функция может быть определена как взвешенная сумма функций времени равных корреляционной функции первичного сигнала. Как следствие этой теории может бать доказана следующая теорема:
Если на интервале интерполяции 
корреляционная функция и ее взвешенная сумма хорошо аппроксимируются полиномом, то использование этого приближения обеспечит среднеквадратическое приближение близкое к идеальному. Т.е. требуется хорошая аппроксимация не всей корреляционной функции, а только ее части, приходящейся на интервал интерполяции (рисунок 3.5).
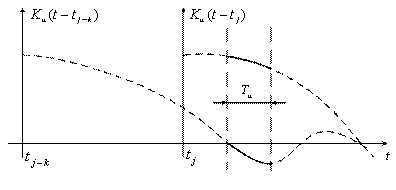
Рисунок 3.5
Чем меньше 
, тем точнее возможна аппроксимация в виде многочлена и тем проще могут быть аппроксимирующие полиномы. Проиллюстрируем эту теорему для сигнала с прямоугольным спектром (рисунок 3.6):
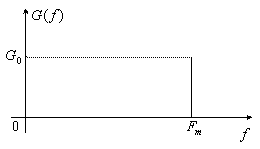
Рисунок 3.6
Известно, что в этом случае в соответствии с теоремой
В.А. Котельникова возможно разложение первичного сигнала в ряд:
, (3.16)
где 
- частота опроса. В точках 
интерполирующая функция равна:
. (3.17)
Сопоставим этот результат с выражением для идеальной интерполирующей функции:
. (3.18)
Чтобы эти формулы совпали, необходимо чтобы при 
, а в случае 
, т. е. чтобы корреляционная функция имела вид:
. (3.19)
Такой функцией корреляции обладает сигнал с прямоугольным спектром, а условие 
при 
приводит к требованию, чтобы частота опроса .
Это соотношение не может быть использовано на практике по следующим причинам:
1. Сигнала с идеальным прямоугольным спектром не существует.
2. Число выборок 
.
На практике при представлении регулярными выборками частота опроса выбирается исходя из соотношения
æ
, (3.20)
где определяется формой спектра сигнала, а æ – коэффициент запаса, зависящий от вида интерполирующих полиномов и требуемых значений показателя верности.
3.4. Интерполяция алгебраическими полиномами
Как было показано выше, для первичных сигналов с разными корреляционными функциями необходимо использовать разные интерполирующие функции. Такой подход не приемлем для практики, т.к. требует выполнения большого объема предварительных работ для определения вида интерполирующих функций. Для преодоления этих затруднений возможны два пути:
1. Использование для группы сигналов с близкими корреляционными функциями интерполирующей функции одного вида.
2. Применение в качестве интерполирующих функций хорошо программируемых функций с выбором частоты опроса, обеспечивающих во всех случаях требуемую верность.
Второй путь наиболее прост, но приводит к завышенным частотам опроса и, следовательно, к увеличению загрузки радиолинии. Наиболее рациональным является комбинированное использование обоих путей.
Во многих случаях в качестве интерполирующих путей используются алгебраические полиномы низких степеней, в частности полиномы Лагранжа. Интерполирующая функция по Лагранжу записывается в следующем виде:
(3.21)
где 
- символ произведения, в котором отсутствуют сомножители при 
. Нетрудно убедиться, что 
при 
и 
при 
.
При интерполяции по Лагранжу требуется определенным образом выбрать интервал обработки 
.
1) Число точек опроса n четное (рисунок 3.7).
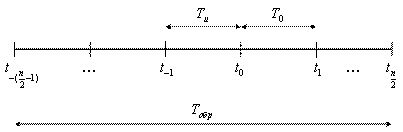
Рисунок 3.7
2) Число точек опроса n нечетное (рисунок 3.8).
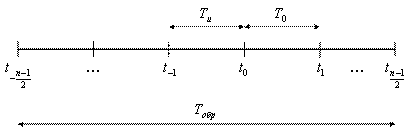
Рисунок 3.8
Запишем момент времени, в котором ищется интерполяционная оценка в виде
, (3.22)
где 
- точка отсчета, - период опроса, 
- безразмерное время, которое может непрерывно изменяться в пределах
, при 
(3.23)
, при 
, 
(3.24)
На практике интерполяция по Лагранжу используется при n = 1, 2, 3:
1. Ступенчатая интерполяция (полиномы нулевой степени ) (рисунок 3.9).
В этом случае n = 1 и для интерполяции используется лишь одна выборка
, 
, 
и 
.
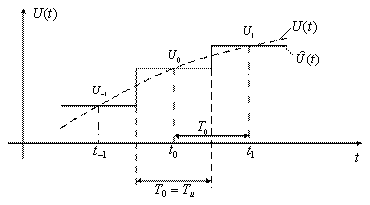
Рисунок 3.9
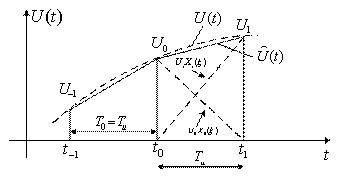
2. Линейная интерполяция (полиномы первой степени) (рисунок 3.10).
При этом 
, 
, 
и интерполирующие функции имеют вид 
, 
.
Рисунок 3.10
3. Квадратичная интерполяция (квадратичная интерполяция) (рисунок 3.11).
При этом 
, 
, 
и интерполирующие функции имеют вид 
, 
, 
.
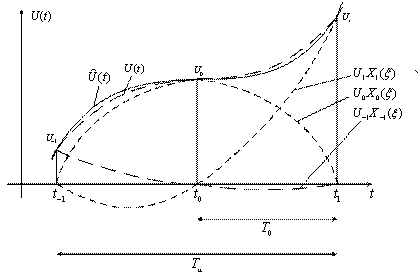
Рисунок 3.11
Можно показать, что верхние оценки относительных ошибок в этом случае равны 
, 
, 
,
где - граничная частота спектра сигнала, - частота опроса.
При 
и 
частота опроса 
, 
, 
.
При восстановлении функции по отсчетам обычно получается плавная кривая, поэтому, можно для практических расчетов выбрать частоту опроса по формуле 
.
3.5. Определение частоты опроса
Определим частоту опроса первичного сигнала при среднем квадратическом приближении алгебраическими полиномами. Используем показатель верности оценки в форме интегральной средней квадратической ошибки
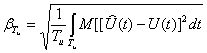. (3.26)
Более удобно использовать приведенный показатель верности:
. (3.27)
Применим эту формулу для определения частоты опроса четырех моделей первичного сигнала: Модель 1. Сигнал с ограниченным равномерным спектром (рисунок 3.12).
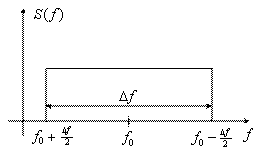
Рисунок 3.12
Применяя косинус преобразование Фурье от 
, получим функцию корреляции этого сигнала:
. (3.28)
Модель 2. Сигнал с треугольным спектром (рисунок 3.13).
, 
.
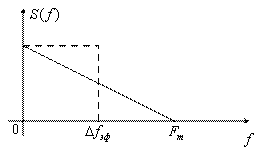
Рисунок 3.13
Эффективная ширина спектра в этом случае имеет вид 
, а функция корреляции равна
. (3.29)
Модель 3. Сигнал марковского типа (рисунок 3.14).
Энергетический спектр этого сигнала описывается соотношением
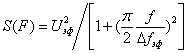, а функция корреляции равна
. (3.30)
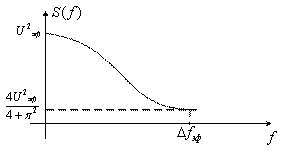
Рисунок 3.14
Модель 4. Сигнал с колокольным спектром (рисунок 3.15). Энергетический спектр этого сигнала описывается соотношением
,
где 
, а функция корреляции равна
. (3.31)
Рисунок 3.15
Эти модели охватывают значительную часть практически используемых сигналов и являются стационарными случайными процессами. Применяя для этих моделей интерполяцию по Лагранжу при 
получим следующие формулы (таблица 3.1) для расчета величины æ = 
.
В случае модели 1 и идеальной интерполяции, т.е. при опросе по В.А. Котельникову, æ = 1. Формулы, приведенные в таблице используются для определения частоты опроса 
= æ
.
Таблица 3.1
| Модель | æ = |
||
|
1 |
n = 1 |
n = 2 |
n = 3 |
|
|
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
Построим графики зависимости æ от показателя верности 
для различных моделей сигналов (рисунки 3.16, 3.17).
Выводы:
1. Для всех моделей, за исключением третьей, интерполяция полиномами более высокого порядка позволяет уменьшить частоту опроса при той же верности.
2. При переходе от линейной интерполяции к квадратичной, уменьшение частоты опроса не столь значительно, как при переходе от ступенчатой интерполяции к линейной.
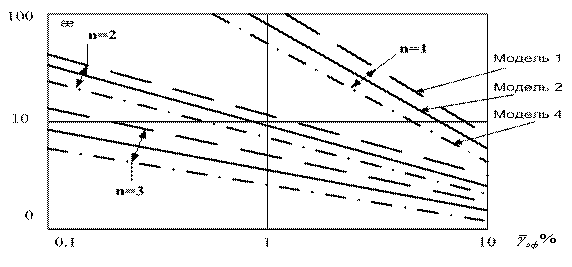
Рисунок 3.16
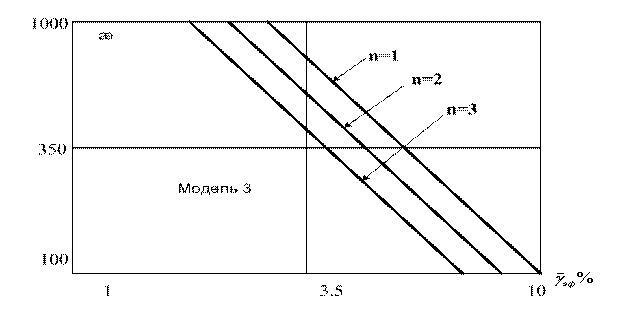
Рисунок 3.17
3. Увеличивать степень полинома целесообразно только при увеличении требований к точности интерполяции.
4. Для третьей модели переход от линейной модуляции к квадратичной нецелесообразен, что объясняется свойствами марковских сигналов.
5. При интерполяции алгебраическими полиномами первичного сигнала коэффициент корреляции между соседними выборками равен 0,85 – 0,995. Это приводит к неэффективному использованию пропускной способности канала передачи информации.
6. Для определения частоты опроса необходимо располагать:
- спектральными характеристиками первичного сигнала, т.е. полосой
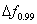по уровню 0,99 энергии сигнала; - точностными характеристиками, т.е. показателем верности
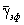%; - задать алгоритм обработки, т.е. тип интерполирующего полинома.
4. Обобщенные дискретные представления
4.1. Вводные замечания
При дискретно – аналоговых представлениях с помощью регулярных выборок для получения малой ошибки интерполяции необходимо выбирать большую частоту опроса. При этом между соседними выборками появляются сильные корреляционные связи, что уменьшает пропускную способность канала передачи информации.
Для сокращения избыточности используют два пути:
1. Отказаться от использования в качестве координат регулярных выборок. При этом увеличивается эффективность представления путем изменения частоты опроса сигнала.
2. Использовать обобщенные дискретные представления, позволяющие сократить количество координат при условии, что корреляционные связи между отдельными отсчетами сигнала на интервале представления
.
При обобщенных дискретных представлениях в результате анализа поведения функции 
на интервале представления 
формируется сообщение:
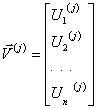, (4.1)
где 
- координаты, формируемые в результате анализа сигнала на интервале представления . Для этого весь интервал наблюдения 
разбивается на интервалы представления 
… и т.д.(рисунок 4.1)
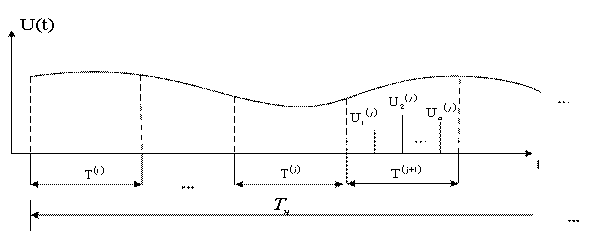
Рисунок 4.1
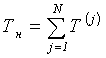. (4.2)
В результате анализа функции на интервале после окончания этого интервала формируется сообщение 
, которое передается в 
интервале представления. Обычно интервал представления выбирается равным:
, (4.3)
где 
- максимальный интервал корреляции, при 
.
Координаты получаются как коэффициенты разложения сигнала в функциональный ряд по базисным функциям 
. (4.4)
На приемной стороне по переданным координатам 
восстанавливается первичный сигнал
, (4.5)
а координаты 
на передающей стороне определяют как коэффициенты функционального ряда:
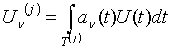, (4.6)
где 
- весовая функция, определенным образом связанная с .
Как следует из этого соотношения координата может быть представлена как результат фильтрации сигнала фильтра с импульсной характеристикой:
. (4.7)
Выбор лучшего обобщенного представления сводится к решению двух задач:
1. Выбор оптимального базиса . 2. Определение числа координат , обеспечивающих заданную точность восстановления функции.
Оптимальные базисы, минимизирующие число координат при заданной точности восстановления, связаны с вероятностными характеристиками первичного сигнала. Они описываются громоздкими выражениями и на практике неудобны. Обычно используют универсальные базисы , применение которых не требует сложных устройств обработки и , в тоже время , достаточно эффективно. Такие базисы выбирают в классе ортогональных функций:
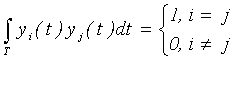. (4.8)
В качестве примера рассмотрим базисные функции в виде полиномов Лежандра и функций Уолша.
4.2. Представления сообщений с помощью полиномов Лежандра
Поместим начало отсчета времени в середину интервала представления:
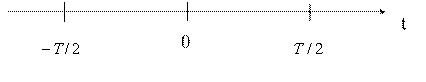
Рисунок 4.2
Введем нормированное время 
.При таких обозначениях полиномы Лежандра задаются соотношением:
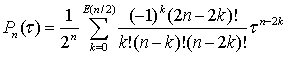, (4.9)
где 
- целая часть n/2. В частных случаях полиномы Лежандра имеют вид:
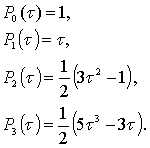(4.10)
Полиномы Лежандра при 
описываются рекуррентным соотношением:
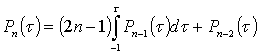. (4.11)
Графики первых четырех полиномов Лежандра приведены на рисунке 4.3:
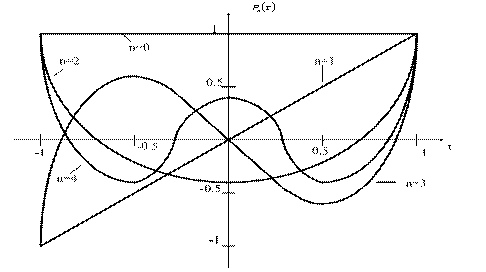
Рисунок 4.3
Структурная схема формирования полинома Лежандра имеет вид (рисунок 4.4):
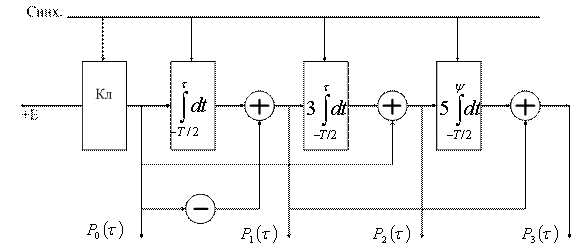
Рисунок 4.4
Структурная схема формирования координат 
изображена на рисунке 4.5, где
, (4.12)
- коэффициенты пропорциональности.
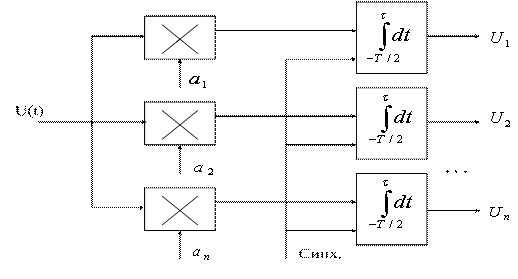
Рисунок 4.5
Недостатки обобщенных представлений с помощью полиномов Лежандра:
- Сложность формирования весовых функций
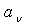. - Необходимость контроля коэффициента усиления каналов формирования координат .
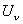- Высокие требования к синхронизации.
При цифровом представлении весовых функций эти недостатки снимаются.
4.3. Представление сообщений с помощью функций Уолша
Использование этих представлений позволяет избежать многих недостатков представления сообщений с помощью полиномов Лежандра. Достоинством является простота реализации таких представлений с помощью цифровой техники.
Выберем начало отсчета времени у левой границы интервала представления (рисунок 4.6).
Рисунок 4.6
Введем нормированное время: 
, 
. При использовании функций Уолша число отсчетов 
следует выбирать так, чтобы выполнялось равенство: 
, где 
-целое число.
Функции Уолша строятся на основе базовых функций следующего вида (рисунок 4.7):
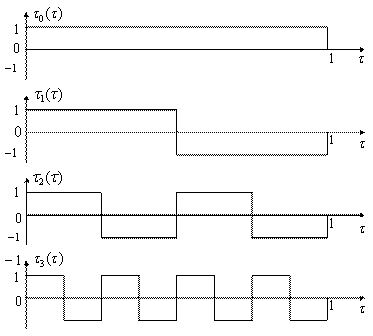
Рисунок 4.7
Базовые функции ортогональны, т.е. для них выполняется следующее условие:
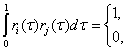
. (4.13)
Все функции Уолша находятся из соотношения:
, (4.14)
где 
, 
, 
- целые числа, 
.
Используя формулу (4.14), определим первые восемь функций Уолша: 1. 
; 2. 
, 
, 
; 3. 
, 
, 
; 4. 
, , 
, 
; 5. 
, 
, 
; 6. 
, , 
, 
; 7. 
, , , 
; 8. 
, , , 
, 
; Построим графики функций Уолша (рисунок 4.8). Функции Уолша также ортогональны:
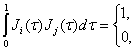
. (4.15)
Формирование функций Уолша возможно с помощью элементов цифровой техники. Структурная схема формирования функций Уолша имеет вид, представленный на рисунке 4.9.
Формирование координат 
производится в соответствии с выражением
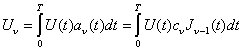. (4.16)
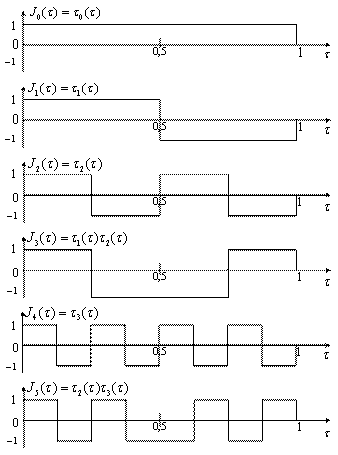
Рисунок 4.8
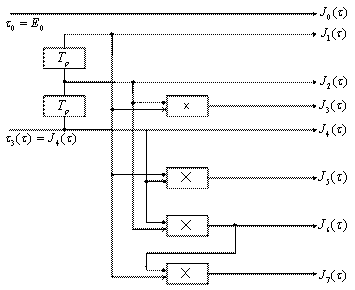
Рисунок 4.9
Недостатки обобщенных представлений с помощью функций Уолша:
1. Требуется большее число координат, чем при представлении с помощью полиномов Лежандра при той же точности.
2. Требуется большая полоса устройств формирования при реализации функций Уолша, чем при полиномах Лежандра.
5. Сжатие данных при телеизмерениях
5.1. Вводные замечания
В системе с циклической дискретизацией избыточность данных возникает даже при правильно выбранной частоте опроса датчиков, т.к. при мало меняющихся во времени параметрах частота опроса остается той же, что и на участках, где такая частота является необходимой. Т.о., целью сжатия данных является формирование минимального количества координат, обеспечивающих воспроизведение первичного сигнала с заданной вероятностью. Для пояснения вышесказанного рассмотрим изменение некоторой функции на интервале представления (рисунок 5.1).
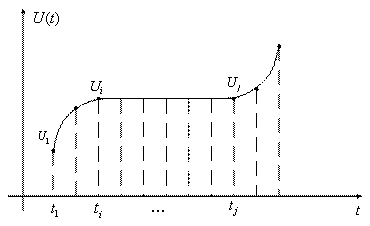
Рисунок 5.1
Передача дискретных значений 
на участке 
дает избыточную информацию о поведении функции . Передача избыточной информации приводит к расширению полосы частот в канале связи, увеличивает время необходимое для обработки информации и расход энергии источника питания.
Т.о., сжатие объема сообщений позволяет:
- Уменьшить требуемую пропускную способность канала передачи информации, а также объем памяти запоминающих устройств.
- Увеличить оперативность получения необходимой информации.
- Уменьшить требования к весу, объему, энергетическим показателям различных устройств РТМС.
Сократить избыточность информации можно в различных сечениях тракта РТМС (рисунок 5.2), где Д – датчики, УСИ – устройство сокращения информации, РТС – радиотехническая система, ЛС – линия связи, УОИ – устройство обработки информации.
Рисунок 5.2
Сжимать информацию можно:
- На выходе Д путем предварительной обработки информации, например, с помощью адаптивной коммутации.
- На выходе РТМС с целью разгрузки системы передачи информации, например, путем рационального кодирования и используя необратимые методы сжатия.
- На входе устройств первичной обработки путем отбора наиболее важной информации.
5.2. Классификация и основные характеристики метода сжатия данных
Существует несколько методов сжатия объема сообщения (рисунок 5.3), где ИИД – исключение избыточных данных, АД – адаптивная дискретизация, АК – адаптивная коммутация, АРЧ – автоматическая регулировка частоты опроса сигнала.
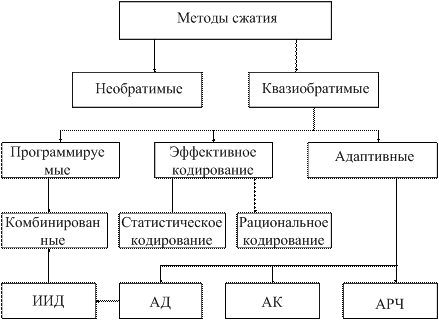
Рисунок 5.3
По возможности восстановления исходного сигнала все методы сжатия делятся на необратимые и квазиобратимые. К необратимым относятся методы, при которых на приемную сторону передается не сам сигнал как функция времени, а какие-то его характеристики. Имея эти характеристики невозможно восстановить исходный сигнал как функцию времени. В качестве таких характеристик могут выступать спектральная плотность мощности, функция плотности вероятности, форма корреляционной функции. К квазиобратимым относятся методы допускающие восстановление исходного сигнала с определенной степенью верности.
Программируемые представления предполагают возможность изменения способа представления или его показателей, например частоты опроса, в ходе работы системы. Смена режима производится или по решению оператора или по определенной программе. Число различных основных показателей такого представления обычно ограничено.
К методам сжатия данных путем эффективного кодирования относятся методы представления измеряемой информации в дискретной форме, требующие минимального количества символов при заданных показателях верности. К эффективному кодированию относится статистическое и рациональное кодирование. Алгоритмы статистического кодирования позволяют сократить число двоичных символов в коде при передаче отдельных фрагментов сообщений с большой вероятностью появления. Например, гласные имеют большую вероятность появления, поэтому их можно кодировать кодом с минимальным количеством символов и наоборот. Алгоритмы рационального кодирования обеспечивают передачу сообщений с минимальным количеством символов при том же качестве восстановления сигналов в условиях априорной неопределенности относительно вероятностных и спектральных характеристик.
Адаптивные методы сжатия данных позволяют уменьшить среднюю частоту дискретизации. Они основаны на кусочной аппроксимации измеряемой величины более простой функцией времени и передаче дискретных значений измеряемой величины при достижении погрешностью аппроксимации некоторого заданного значения. Для реализации адаптивных методов могут применяться адаптивная коммутация каналов, адаптивная дискретизация и исключение избыточных данных. Возможно применение комбинированного метода, сочетающего в себе принципы программируемых систем и систем, исключающих избыточные данные. В некотором случае целесообразно применять РТМС с автоматическим регулированием частоты опроса датчиков. Адаптивные методы делятся на одно- и двухпараметрические. В случае однопараметрической адаптации может фиксироваться длительность интервала сообщения и тогда изменяется число формируемых координат или может фиксироваться число формируемых координат и тогда изменяется длительность интервала сообщения. При двухпараметрической адаптации изменяется число формируемых координат и длительность сообщений. РТМС со сжатием данных характеризуется рядом коэффициентов:
1. Коэффициент сжатия данных - определяется как отношение 
отсчета измеряемой величины, передаваемой без сжатия, к количеству отсчетов 
в системе со сжатием, за продолжительность времени 
при заданной верности :
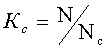. (5.1)
Существует информационная трактовка этого коэффициента:
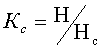, (5.2)
где 
- количество передаваемой информации в системе без сжатия, 
- среднее количество передаваемой информации в системе со сжатием.
2. Коэффициент эффективности, позволяющий получить сравнительную оценку различных методов сжатия.
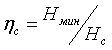, (5.3)
где 
- минимальное количество информации, которое при заданном ограничении, например, длительности интервала представления, необходимо передавать в системе. Коэффициент эффективности является абсолютной характеристикой способа представления сообщения в данном классе.
3. Коэффициент помехоустойчивости, характеризующий чувствительность сообщения к искажению координат
(5.4)
где 
- значения показателя верности в системе без сжатия и со сжатием данных. Помехоустойчивость системы может характеризоваться коэффициентами сжатия по полосе и мощности.
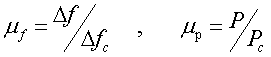, (5.5)
где 
- полоса частот и мощность источника питания на передающей стороне в системе без сжатия и со сжатием данных, обеспечивающие ту же верность.
4. Время задержки сообщения в аппаратуре сжатия - 
. На этот параметр накладываются ограничения, определяемые временем протекания аварийных процессов, т.к. в этом случае вся накопленная в оперативной памяти информация может быть потеряна.
5. Коэффициент сложности алгоритма - характеризует среднее число вычисляемых операций или команд, реализуемых аппаратурой сжатия данных для вычисления одной координаты.
5.3. Программируемые РТМС
В рассматриваемых РТМС сокращение избыточности достигается за счет установления на некотором отрезке времени для каждого параметра или группы параметров своей частоты опроса. Установка частоты опроса 
осуществляется по известным максимальным характеристикам параметров: граничной частоты спектра, минимальным интервалом корреляции и максимальной скорости изменения параметра. Для программного изменения частоты опроса должны быть известны указанные априорные сведения. На рисунке 5.4 показано, что на интервалах 
частота опроса меняется дискретно.
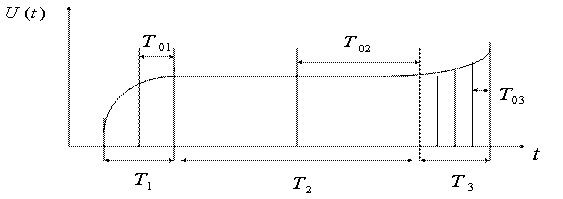
Рисунок 5.4
Скачкообразное изменение частоты опроса позволяет сократить избыточность, сохраняя заданное значение погрешности дискретизации.
Структурная схема передающей части программируемой РТМС представлена на рисунке 5.5, где Д – датчики, К – коммутатор, РПУ – радиопередающее устройство, УУ+ЗУ – устройство управления и запоминающее устройство.
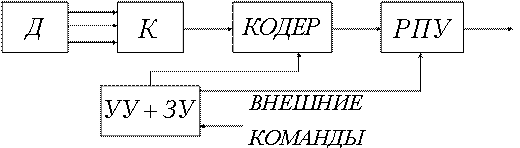
Рисунок 5.5
Управляющие сигналы поступают на вход коммутатора, кодирующего устройства и передатчика, изменяя их характеристики. Программа управления хранится в ЗУ и обновляется по внешним командам.
Недостатки программируемых РТМС:
- Необходимость наличия априорных сведений об измеряемых параметрах.
- Дискретное изменение частоты опроса, ведущее к некоторой избыточности.
Достоинства программируемых РТМС:
- Простота реализации и высокая информационная гибкость.
- Сокращение объема передаваемых данных за счет сокращения избыточности по множеству параметров.
5.4. Адаптивные методы сжатия
5.4.1. Алгоритмы полиноминальных методов сжатия
На основе полиноминальных методов сжатия данных разработаны алгоритмы адаптивной дискретизации и исключения избыточности данных. В отличие от методов регулярных выборок при использовании полиноминальных методов сжатия точка опроса не образует периодической последовательности. В этом случае передаются и запоминаются существенные выборки (рисунок 5.6).
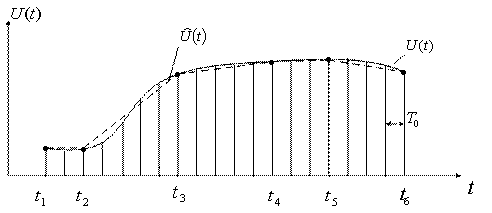
Рисунок 5.6
Под существенными выборками понимаются выборки, позволяющие получать на приемной стороне первичный сигнал с заданной точностью. Т.к. существенные выборки не образуют регулярную последовательность, то для получения оценки первичного сигнала необходимо передавать дополнительную информацию в виде значений времени … появления существенных выборок. Для формирования существенных выборок обычно используется кусочная аппроксимация измеряемых величин алгебраическим полиномом.
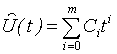, (5.6)
где - коэффициенты полинома.
Для реализации полиноминальных методов сжатия необходимо устройство, определяющее погрешность аппроксимации и изменяющее режим работы системы, т.е. частоту опроса. В зависимости от типа преобразователей погрешности аппроксимации известны экстраполяционные и интерполяционные алгоритмы адаптивного сжатия.
5.4.2. Экстраполяционные методы сжатия
Сущность метода экстраполяции, т.е. предсказания, заключается в получении упрежденных значений параметра на основе предшествующих данных. Если текущее значение параметра отличается от предшествующего не больше, чем на величину заданного допуска, то оно отбрасывается. Для предсказания (
)-го отсчета, если известны предыдущих отсчетов используется формула:
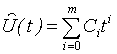. (5.7)
В зависимости от степени полинома различают предсказатели нулевого, первого и т.д. порядка. Рассмотрим предсказатель нулевого порядка (рисунок 5.7). В этом случае степень полинома 
, а предсказанное значение 
. Таким образом, если имеется отсчет 
, то предполагается, что последующие отсчеты 
и т.д. равны .
Относительно величины отсчета устанавливается зона 
. Эта зона называется зоной сравнения или апертурой. Для каждого 
-го отсчета, следующего за 
-ым существенным отсчетом, вычисляется разность:
. (5.8)
Рисунок 5.7
Отсчет считается существенным, если 
. Сжатие с помощью полинома нулевого порядка требует запоминание последнего существенного отсчета. Блок - схема алгоритма данного метода показана на рисунке 5.8.
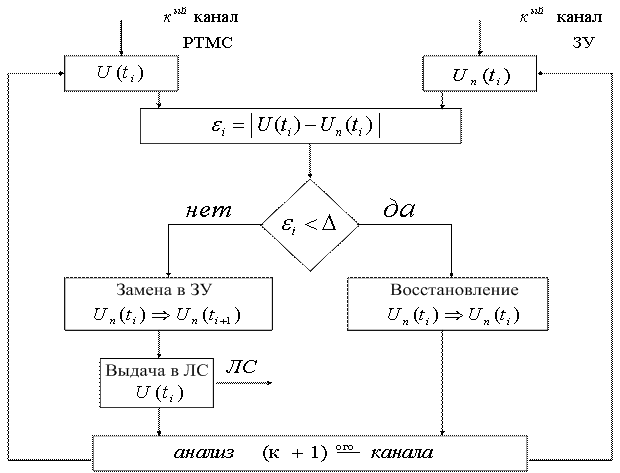
Рисунок 5.8
Рассмотрим теперь предсказатель первого порядка. Степень полинома в этом случае m=1. Для построения полинома требуется два предшествующих отсчета, через которые проводится прямая линия. Предсказанное значение для последующих отсчетов лежит на этой линии (рисунок 5.9).
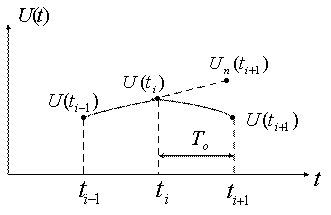
Рисунок 5.9
Предсказанное для момента времени 
значение параметра рассчитывается по формуле:
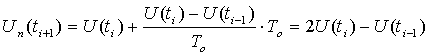. (5.9)
Если ошибка 
, то отсчет исключается. В этом случае для расчета предсказанного значения в точке 
используется формула:
. (5.10)
Сжатие с помощью предсказателя первого порядка требует запоминание последнего существенного отсчета и предсказанного значения отсчета (рисунок 5.10).
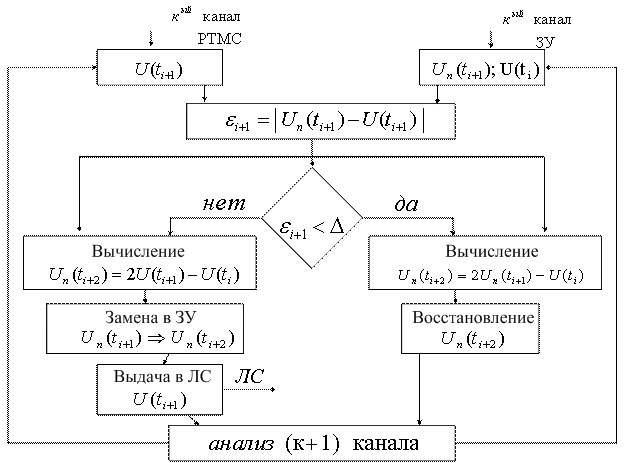
Рисунок 5.10
Согласно экспериментальным данным при сжатии медленно меняющихся параметров предсказатель нулевого порядка дает коэффициент сжатия около 50, а предсказатель первого порядка – 70. Использование полиномов более высокого порядка даёт небольшое приращение коэффициента сжатие, но приводит к увеличению вычислений и усложнению экстраполятора. Наиболее помехоустойчивы экстраполяторы низких порядков, поэтому обычно используются экстраполяторы нулевого и первого порядка.
5.4.3. Оптимальное линейное предсказание
Для определения алгоритма оптимального линейного предсказания необходимо знать корреляционную функцию или энергетический спектр параметра. Значения параметра в момент времени предсказывается путем вычисления линейной комбинации предшествующих отсчетов по формуле:
, (5.11)
где коэффициенты 
выбираются из условия минимальной дисперсии разности предсказанного значения от действительной величины.
. (5.12)
Коэффициенты находятся путем решения системы уравнений вида:
, 
(5.13)
В случае если используется одно предшествующее значение параметра , то
, 
, (5.14)
где 
- коэффициент корреляции параметра, - период опроса.
Если используется два предшествующих значения параметра :
, 
(5.15)
Алгоритм работы при оптимального линейного предсказания строится также, как и при предсказании нулевого и первого порядка, но вычисление предсказания параметра осуществляется в соответствии с формулами (5.14) и (5.15).
Можно показать, что дисперсия отклонения предсказанного значения от действительного в случае предсказания нулевого порядка:
, (5.16)
а в случае предсказания первого порядка:
. (5.17)
5.4.4. Интерполяционные методы сжатия
Предсказание эффективно в том случае, если параметр плавно изменяется по времени. Если параметр искажается шумом или имеет быстрое изменение, то эффективность методов сжатия, основанных на предсказаниях, существенно снижается. В этом случае использование интерполяционных методов сжатия позволяет исключить большее число избыточных отсчетов. Сущность методов интерполяции состоит в замене параметров аппроксимирующей функцией вида:
(5.18)
Обычно в качестве таких функций используются полиномы нулевого и первого порядков.
Применение полиномов более высокого порядка приводит к резкому увеличению объема вычислений и не дает значительного приращения коэффициента сжатия.
Рассмотрим интерполяцию нулевого порядка. При этом 
и аппроксимирующей функцией является прямая линия параллельная оси абсцисс.
На отрезке интерполяции 
находится минимальное 
и максимальное 
значение параметров. Интерполяционная прямая равна:
(5.19)
Рассмотрим особенности в случае применения интерполяционного и экстраполяционного методов сжатия данных (рисунок 5.11).
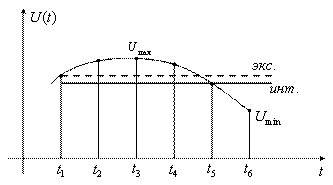
Рисунок 5.11
Для определения величины интерполяционного интервала произведем вычисление погрешности интерполяции
(5.20)
для все увеличивающегося интервала наблюдения.
Как только 
, то полученный интервал фиксируется. Обычно при экстраполяции ошибка аппроксимации параметра получается больше 
, а 
. Это объясняется тем, что при интерполяции значение существенного отсчета вычисляется в конце интервала интерполяции, т.е., с учетом не только предшествующего, но и последующего отсчетов. При экстраполяции существенным является первый отсчет. Но при интерполяции необходимо произвести больший объем вычислений, чем при экстраполяции. При интерполяции первого порядка в качестве интерполирующей функции используется прямая, которая может иметь произвольный наклон.
5.4.5. Сравнение полиномиальных методов сжатия
Основными факторами, определяющими применимость того или иного метода сжатия являются:
- эффективность изменения избыточности;
- сложность реализации алгоритмов сжатия данных.
Величина коэффициента сжатия зависит от алгоритма и определяется шириной апертуры, которая задает точность восстановления, а также характером изменения параметра. Последняя причина является очень существенной. При одной и той же апертуре в зависимости от характера изменения параметра коэффициент сжатия изменяется от десятков до сотен. Для ориентировочных расчетов можно использовать данные о коэффициенте сжатия, полученные при испытаниях ракеты “Поларис”.
На рисунке 5.12 представлены зависимости коэффициента сжатия от величины апертуры для трех алгоритмов.
ИПП – интерполятор первого порядка
ИНП – интерполятор нулевого порядка
ПНП – предсказатель нулевого порядка
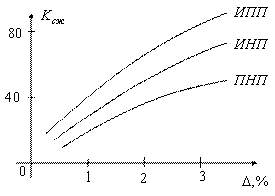
Рисунок 5.12
При использовании алгоритмов сжатия можно передавать данные, занимающие полосу 80 кГц в реальном масштабе времени в полосе телефонного канала 3,2 кГц.
При осуществлении сжатия возможно комбинированное использование нескольких алгоритмов, например, путем экстраполяции или интерполяции нулевого или первого порядка. Для одних участков изменения параметра большей эффективностью будет обладать первый алгоритм, а для других – второй.
Для сравнения рассмотрим следующие классы алгоритмов квазиобратимого сжатия.
1 – ПНП (предсказатель нулевого порядка);
2 – ППП (предсказатель первого порядка);
3 – ИНП (интерполятор нулевого порядка);
4 – ИПП (интерполятор первого порядка);
5 – ПНП-ИПП (комбинированный алгоритм)
6 – комбинированный алгоритм ИНП-ИПП.
Для удобства анализа критерии качества исследуемых алгоритмов относились к соответствующим значениям алгоритма ПНП.
Сложность аппаратурной реализации оценивалась количеством интегральных микросхем (МК), необходимых для построения устройства, или количеством элементарных операций (ОП) на обработку одного отсчета, или объемом оперативной памяти запоминающего устройства (ЗУ), требуемый для обработки одного параметра (рисунок 5.13).
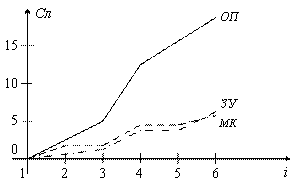
Рисунок 5.13
Получены значения коэффициента сжатия данных, полученные при анализе данных поступающих с космического аппарата Луна-15 (рисунок 5.14).
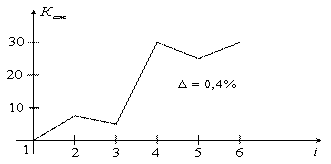
Рисунок 5.14
Для алгоритмов 1, 2, 3 коэффициент сжатия пропорционален сложности реализации. Причем, сложность интерполятора (алгоритм 3) выше, чем у алгоритма 1. Алгоритм 4 (ИПП) обеспечивает коэффициент сжатия примерно 30, а затраты реализации в 4 раза превышают затраты на построение алгоритма 1. Наиболее простая техническая реализация у алгоритма ППП и алгоритма ИПП, когда гладкие процессы, и алгоритма ИПП, когда шумовые процессы.
Полиномиальные методы сжатия данных реализуются в конкретных адаптивных системах.
6. Структурная схема адаптивной системы сжатия данных
6.1. Общие сведения
Введение адаптации в РТМС может привести к ряду преимуществ. Например, возможно уменьшить объем памяти и число регистрирующих устройств на земле, а при уменьшении частоты коммутации использовать менее быстродействующие коммутационные элементы. Для решения задачи измерения и передачи ряда параметров можно использовать различные адаптивные РТМС. Сравнение этих РТМС обычно осуществляют по следующим критериям:
- конструктивному;
- метрологическому;
- экономическому.
Конструктивный критерий рассматривает техническую осуществимость данной системы с точки зрения реализации следующих характеристик РТМС:
- Числа параметров при заданной пропускной способности канала связи.
- Необходимой скорости передачи информации при заданной допустимой задержке.
- Используемого способа сжатия.
- Возможности восстановления предаваемой информации на принимаемой стороне.
Метрологический критерий рассматривает предельное значение:
- Показателя вероятности.
- Вероятности появления заданной погрешности представляемой информации устройств сжатия данных.
- Значения погрешности, появившейся от введения устройств сжатия данных.
- Помехоустойчивости системы.
Экономический критерий рассматривает целесообразность введения адаптации в РТМС, т.е. определяет экономический выигрыш от сжатия информации. При введении адаптации в РТМС уменьшаются требуемая полоса частот КС, объем памяти системы, объем регистрируемых данных, масса бортовой аппаратуры, но сама система усложняется, поэтому возрастает ее стоимость.
Сравнение различных адаптивных РТМС необходимо производить при заданных статистических моделях параметров и заданных условиях функционирования всей системы. Обычно экономический эффект от внедрения системы сжатия данных составляет около 10% от стоимости всей системы, например, для системы “Аполлон” стоимостью 20 млд. $ экономический эффект от внедрения системы сжатия данных составил 240 млн. $.
6.2. РТМС с адаптивной дискретизацией
Назначением данных РТМС является согласованием характеристик входного потока сообщений с характеристиками канала передачи. Обычно большой объем измерительных сообщений необходимо предавать по КС с ограниченной полосой пропускания. Известно, что погрешность представления информации, быстродействие РТМС и полоса частот КС связаны соотношением:
, (6.1)
где 
- число уровней квантования измеряемой величины, - период дискретизации, определяющий быстродействие системы, 
- полоса частот КС, 
- мощность сигнала и шума в КС.
Выражение показывает, что при сохранении заданной погрешности уменьшение полосы частот канала передачи требует увеличения периода дискретных сигналов и наоборот.
Это обстоятельство позволяет предложить простой способ сжатия данных по полосе частот КС в случае, когда полоса частот КС 
меньше требуемой полосы частот.
(6.2)
6.2.1. РТМС со сжатием данных по полосе
Структурная схема РТМС со сжатием данных по полосе имеет следующий вид (рисунок 6.1):
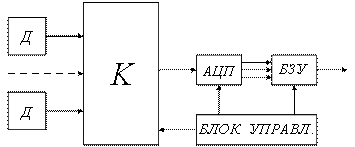
Рисунок 6.1
Схема состоит из источников сообщений в виде датчиков 
, коммутатора 
, буферного запоминающего устройства 
и блока управления. Вся информация с АЦП записывается в со скоростью, соответствующей максимальной частоте дискретизации сигнала. Память должна обеспечить запись всей информации. Считывание информации из в канал передачи осуществляется с меньшей скоростью, чем при записи в соответствии с полосой пропускания частот канала передачи.
Достоинство этой схемы: простота и отсутствие служебной информации о номере передаваемого канала, т.к. в этом случае производится циклическая передача и нумерация каналов не нарушается.
Недостатком схемы является невозможность получить высокий коэффициент сжатия по полосе и больший объём . Для получения более высоких коэффициентов сжатия необходимо предварительное сокращение избыточной информации до её записи в . Это уменьшит объём памяти и время задержки информации.
Возможны два варианта построения адаптивных РТМС с предварительным сокращением избыточной информации:
- Устройство сокращения данных имеется в каждом измерительном канале.
- Устройство сокращения данных находится после коммутатора или после АЦП.
6.2.2. РТМС с адаптивной дискретизацией в каждом канале с буферной памятью
В данной РТМС частота выдачи отсчета по каждому контролируемому параметру является функцией характера его изменения и определяется допустимой погрешностью измерения
. (6.3)
Рассмотрим иллюстрацию работы РТМС с адаптивной дискретизацией при использовании ступенчатого метода восстановления параметра, т.е. при использовании экстраполяции нулевого порядка (рисунок 6.2).
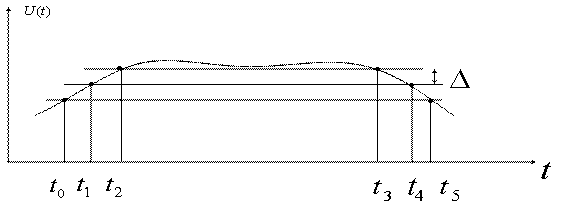
Рисунок 6.2
На выходе временного адаптивного дискретизатора поток отсчетов будет неравномерным, но всегда выполняется условие, что
, где 
(6.4)
Нумерация каналов в этом случае также случайная.
Рассмотрим первый вариант построения РТМС с адаптивной дискретизацией (рисунок 6.3).
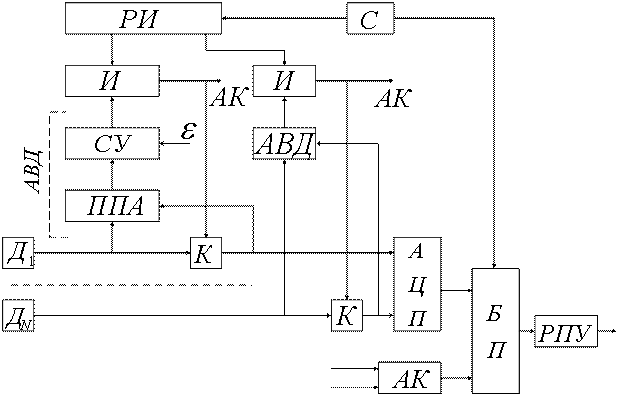
Рисунок 6.3
Сигналы с датчиков поступают в адаптивные временные дискретизаторы (
), состоящие из преобразователя погрешности аппроксиматора (
) и сравнивающего устройства (
).
функционирует в соответствии с одним из полиноминальных методов сжатия данных.
На 
подаётся пороговое напряжение 
, соответствующее допустимой погрешности аппроксимации. При равенстве сигнала с ППА и , 
выдает сигнал на схему «
», на которую поступают также сигналы от распределителя импульсов (
). 
осуществляет расстановку отсчетов каждого параметра на временной оси. Сигнал со схемы «
» поступает на ключ 
, пропускающий измерительную информацию в кодирующее устройство - 
и далее в буферную память (
). Одновременно в 
вводится номер канала – адрес кода 
. Отсчеты во всех каналах расположены через различные промежутки времени. выдает отсчеты в РПУ через одинаковые интервалы времени.
Достоинства РТМС с адаптивной дискретизацией:
- возможность получения высоких коэффициентов сжатия при уменьшении объёма буферной памяти;
- возможность приоритета обслуживания отдельного канала путем регулировки порога
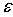отдельных каналов.
Недостатки:
- измерительная информация передаётся в ненатуральном масштабе времени;
- полное нарушение закономерной выдачи отсчетов, что приводит к усложнению аппаратуры;
- применение аналоговых
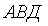; - необходимость использования дискретизатора для каждого канала;
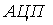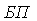- высокие требования к быстродействию и , особенно при большом числе каналов, когда возрастает вероятность совпадения отсчетов на его входе и возможность переполнения
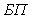; - появление дополнительной погрешности из-за возможного запаздывания опроса канала, в котором
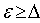, но импульс с 
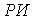приходит в другой канал.
Рассмотрим второй вариант построения РТМС с адаптивной дискретизацией. Обычно их называют РТМС с исключением избыточных данных.
6.2.3. РТМС с исключением избыточных данных
В таких РТМС применяются цифровые 
. В начале с помощью коммутатора производится аналогично системе с временным разделением каналов циклический опрос датчиков (рисунок 6.4), где УУ – управляющее устройство.
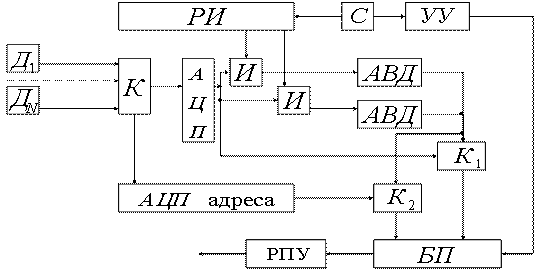
Рисунок 6.4
преобразуют каждый отсчет в кодовую форму. Выделение отсчетов соответствующих каналов для обработки в осуществляется в схеме «». Сигналы с выхода 
и 
открывают ключи 
и 
, полученные существенные отсчеты и соответствующие им адреса кодовых комбинаций с выходов ключей и записываются в . С помощью 
производится равномерное считывание отсчетов из . Отсчеты запоминаются в и относительно последнего существенного отсчета устанавливается зона допуска .
Достоинства РТМС с исключением избыточных данных:
- Выдача существенных отсчетов осуществляется в соответствии с нумерацией каналов в цикле, что упрощает построение приемной и передающей аппаратуры.
- При высокой частоте опроса параметров эффективность данной РТМС приближается к эффективности РТМС с адаптивной дискретизацией. При этом рассматриваемая система оказывается более простой.
- Применение цифровых
.
Недостатки РТМС с исключением избыточных данных:
- Применение быстродействующих
. - Необходимость обеспечение устойчивой синхронизации.
- Необходимость обеспечения высокой помехоустойчивости передаваемых данных.
- Возможность переполнения
.
При переполнении происходит потеря отсчетов. С другой стороны, при полном опустошении в канал связи будет передаваться нулевая информация, так называемые «пустые слова», что нежелательно. Для устранения этого недостатка разработаны схемы РТМС с адаптивной дискретизацией в каждом канале без буферной памяти.
6.2.4. РТМС с адаптивной дискретизацией в каждом канале без буферной памяти
Рассмотрим структурную схему данной РТМС (рисунок 6.5).
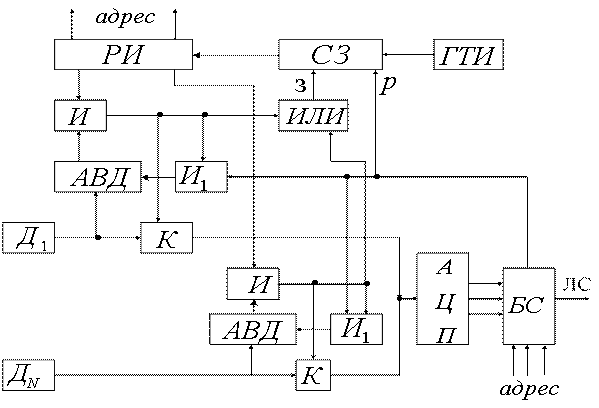
Рисунок 6.5
Достоинством данной схемы является отсутствие буферной памяти, что позволяет производить передачу информации в реальном масштабе времени. Иногда данную систему называют асинхронно - циклической.
Схема работает следующим образом. С помощью в каждом канале, работающем в соответствии с одним из полиноминальных методов сжатия, осуществляется адаптивная дискретизация. Если погрешность аппроксимации в каждом канале:
, (6.5)
то на выходе появляется единица.
В тоже время импульсы от 
через открытую схему запуска (
) с помощью 
поочередно поступают на схему совпадения «
». На выходе схемы «» k – го канала формируется единица, которая открывает ключ (
) и соответствующий датчик подключается к . При этом через собирательную схему «
» подается сигнал запрета (З) на схему запуска, запрещающий прохождение импульсов с до окончания выдачи кода в линию связи. Распределитель импульсов останавливается и выдает номер (адрес) выбранного канала в блок считывания 
. В код адреса и код параметра преобразуются из параллельного кода в последовательный и передаются в линию связи (
). По окончания считывания выдает сигнал на разрешение дальнейшего прохождения импульсов через схему запуска на распределитель, а также на один из входов схемы совпадения «
». Схема «
» служит для формирования сигнала сброса в момент отсчета. Т.к. на второй вход схемы «
» поступает сигнал от схемы «
» своего канала, то сброс производится только в выбранном канале. После этого распределители продолжают опрос схем «». В асинхронно - циклических системах можно не передавать код адреса, а вместо него через канал связи передаются на приемник импульсы переключения распределителя РИ от схемы запуска СЗ. Для предотвращения передачи нулевой информации может быть использована обратная связь от блока считывания к , где осуществляется регулировка допустимой погрешности аппроксимации.
Недостатком такой системы является сложность аппаратуры.
6.2.5. Комбинированные РТМС
В случае, если возможно управление с помощью программного устройства режимами работы РТМС с исключением избыточности данных, то такая система относится к комбинированным РТМС. (рисунок 6.6), где ПК – программируемый коммутатор, УСИ – устройство сжатия информации.
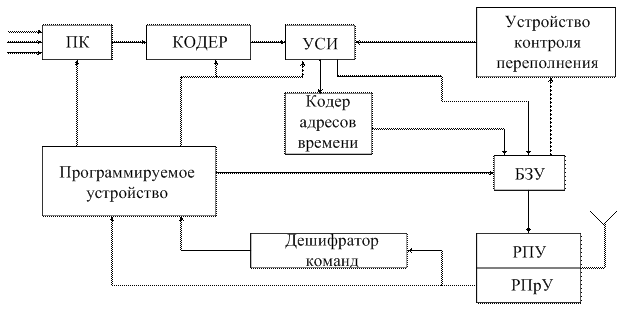
Рисунок 6.6
Отличительными особенностями этой системы являются:
- Управление работой по программе или командам, передаваемым по обратному каналу.
- Изменение частоты опроса коммутатора и связанное с этим сокращение объема вычислений.
- Изменение структуры кода.
- Возможность изменения программ измерений и алгоритмов сжатия данных при передаче.
- Контроль переполнения БЗУ и изменение скорости считывания данных.
6.3. РТМС с адаптивной коммутацией каналов
6.3.1. Обобщенная структурная схема
Адаптивная коммутация представляет собой способ изменения частоты опроса источников информации в соответствии со скоростью изменения входного сигнала. Основной проблемой системы сжатия информации является объединение потоков отсчетов, идущих с различной частотой в единый поток, следующий с постоянной частотой, определяемой пропускной способностью КС.
Очередность передачи информации от различных источников обычно производится в соответствии с такими характеристиками:
- наибольшая текущая погрешность аппроксимации;
- экстремальные значения входных сигналов или их производных;
- отклонение параметров от нормы.
Системы адаптивной коммутации позволяют учитывать приоритет отдельных сообщений по отношению к другим источникам. В системах адаптивной коммутации информация передается в КС в натуральном масштабе времени, т.е. без задержки, что является основным преимуществом таких систем.
В данных системах производится предварительный опрос всех каналов, выявляется канал с наибольшей погрешностью аппроксимации, и информация этого канала поступает в линию связи.
Рассмотрим обобщенную структурную схему системы (рисунок 6.7):
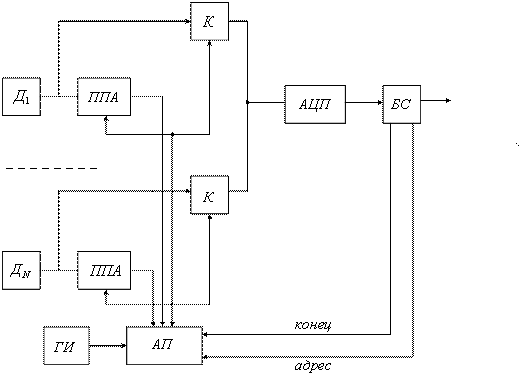
Рисунок 6.7
В каждом измерительном канале имеется преобразователь погрешности аппроксимации (ППА), работающий в соответствии с одним из алгоритмов полиномиального метода сжатия. Анализатор погрешности аппроксимации (АП) путем последовательного опроса ППА выявляет канал с наибольшей погрешностью аппроксимации и открывает ключ (К) данного канала. Далее сигнал кодируется в АЦП и в параллельном коде поступает в блок считывания (БС), куда также поступает и адрес канала. В БС производится преобразование параллельного кода в последовательный, а также помехоустойчивое кодирование. Выдача отсчетов в линию связи производится через равные интервалы времени. После выдачи отсчета в линию из БС в АП поступает сигнал “конец” и сбрасывает АП. Далее операция повторяется.
Достоинства РТМС с адаптивной коммутацией каналов:
- Возможность получения существенного сжатия за счет реализации эффективных методов аппроксимации, при этом коэффициент сжатия АК меньше коэффициента сжатия АД.
- Равномерность следования отсчетов на выходе РТМС, что позволяет обойтись без буферной памяти.
Недостатки РТМС с адаптивной коммутацией каналов:
- Некоторая сложность блока анализатора погрешности аппроксимации.
- Возможность равенства погрешности аппроксимации в нескольких каналах, увеличивающая погрешность телеизмерений.
- При ошибках аппроксимации
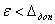будут передаваться избыточные отсчеты, а при 
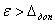будут возникать потери важных отсчетов.
Рассмотрим более подробно пути построения блока АП. Возможны три способа анализа погрешности аппроксимации:
- параллельный;
- последовательный;
- параллельно-последовательный.
Наибольшим быстродействием и простотой обладает АП в случае параллельного анализа погрешности аппроксимации.
6.3.2. РТМС с адаптивной коммутацией каналов при параллельном анализе погрешности
Рассмотрим один из вариантов построения структурной схемы системы (рисунок 6.8), где ВМС – выявитель максимального сигнала.
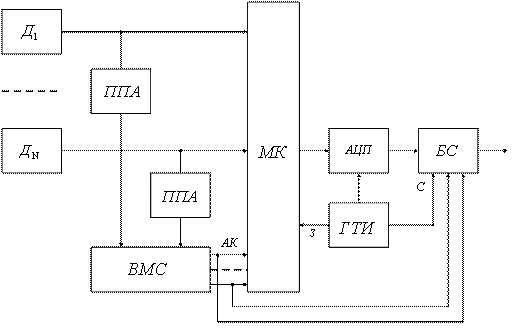
Рисунок 6.8
Сигнал с датчиков поступает на вход ППА и мультиплексора (МК). Мультиплексор находится в закрытом состоянии и открывается с поступлением тактовых импульсов с ГТИ.
Мультиплексор – это устройство, предназначенное для передачи сигналов с любого из входов на одну общую выходную шину.
Вход, с которого сигнал передается на выход, выбирается в зависимости от вида параллельного двоичного кода, подаваемого на управляющие входы. Сигнал с выхода ППА анализируется в блоке выявителя максимального сигнала (ВМС), который представляет собой схему сравнения на N входов. На выходе ВМС формируется параллельный двоичный код, соответствующий номеру канала с наибольшей погрешностью аппроксимации. При поступлении на МК тактовых импульсов с ГТИ на выход проходит сигнал канала, двоичный код номер которого воздействует на управляющие входы МК. После преобразования в АЦП сигнал в параллельном коде, а также код адреса записывается в память БС. При поступлении импульса считывания с ГТИ в БС происходит преобразование параллельного кода в последовательный, и сигнал передается в линию связи.
Рассмотрим простейшую схему ВМС с использованием диодных сборок (диодных схем ИЛИ) и операционных усилителей (ОУ), выходные сигналы которых являются двоичным кодом канала с максимальной погрешностью аппроксимации. Использование диодных сборок для выделения максимального напряжения основан на том, что между операциями алгебры логики и операциями выделения максимума и минимума существует аналогия. Действительно операция объединения соответствует нахождению максимума, а операция пересечения – минимуму.
.
При построении схемы ВМС необходимо учитывать, что в случае соединения соответствующих входов ОУ при наличии максимального сигнала на одном из входов 
соединение должно осуществляться исходя из следующих правил (рисунок 6.9):
. (6.6)
При достаточном усилении ОУ, когда напряжение на прямом входе больше напряжения на инверсном входе, ОУ находится в режиме насыщения, и на выходе формируется единица. Если наоборот, то ОУ находится в режиме отсечки, и на выходе формируется нуль. Для получения хороших результатов в этом случая необходимо, чтобы характеристики диодов были одинаковыми, поэтому применяют диодные сборки, а коэффициент усиления был не меньше 1000.
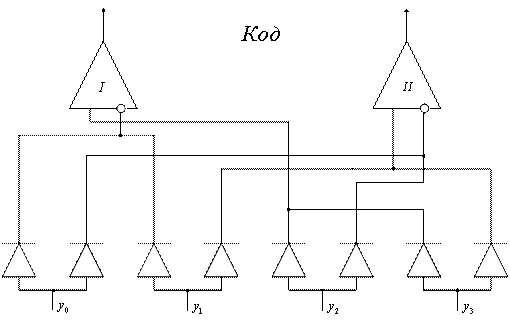
Рисунок 6.9
6.4. РТМС с автоматическим регулированием частоты опроса датчиков
В этих РТМС предусматривается возможность установления различной частоты опроса датчиков, например, в системе МКТ - 1. Так, при аварийных ситуациях увеличение частоты опроса датчиков позволяет получить более подробную измерительную информацию о происходящих в контролируемом объекте процессов. При ручном переключении частоты опроса датчиков есть значительная вероятность опоздать с этим переключением.
Рассмотрим одну из возможных схем устройства для автоматического регулирования частоты опроса датчиков (рисунок 6.10).
Сигнал от датчиков поступает на вспомогательный коммутатор К1 и коммутатор К2. К коммутатору К2, работающему синхронно и синфазно с коммутатором К1 , подключают генератор импульсов (ГИ). Частота генератора импульсов ГИ выбирается много больше, чем максимальная частота спектра сигнала.
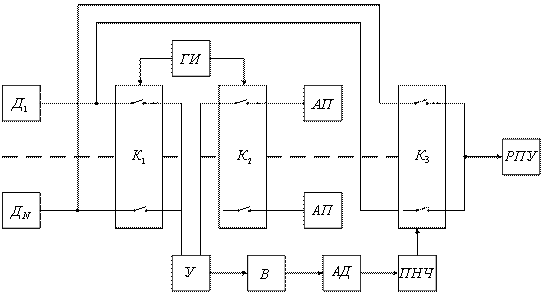
Рисунок 6.10
В дифференциальном усилителе (У) происходит сравнение значения напряжения 
с 
, взятым из ячейки аналоговой памяти. После выпрямления разностного сигнала в выпрямителе (В) этот сигнал поступает на амплитудный дискриминатор (АД), определяющий в каком из каналов наибольшая разность. Далее сигнал поступает на преобразователь напряжение-частота (ПНЧ). Частота переключений первичного сигнала коммутатора К3 будет определяться каналом с наиболее быстро изменяющейся измеряемой величиной, что приводит к образованию избыточной информации в других каналах.
Определим частоту дискретизации 
коммутатора К3 при предположении, что изменяется сигнал только в одном датчике.
Если приращение сигнала за время опроса 
всех датчиков коммутаторами 
и 
определяется выражением:
, (6.7)
то частота дискретизации равна:
, (6.8)
где 
- минимальная частота дискретизации 
, 
- коэффициент регулирования. Частота опроса коммутаторов 
и 
равна:
. (6.9)
Требуется определить значение коэффициента регулирования . Приращение функции можно заменить приближенным выражением:
, (6.10)
где 
- первая производная 
.
При условии 
, тогда:
, (6.11)
, (6.12) Таким образом, частота дискретизации равна:
. (6.13)
Частоты 
выбирают исходя из требований к точности алгоритма интерполяции.
Недостаток РТМС с автоматической регулировкой частоты опроса датчиков: низкий коэффициент сжатия и сложность радиоприемного устройства. Усложнение структуры приемного устройства определяется тем, что отсчеты появляются не в тактовых точках.
7. Методы рационального кодирования
7.1. Вводные замечания
Методы рационального кодирования предназначены для сокращения избыточности сообщений в условиях априорной неопределенности относительно статистических характеристик сигналов [4]. Т.е. в условиях, когда сигнал является нестационарным, что часто встречается на практике, или когда неизвестны статистические характеристики этого сигнала. Под рациональным кодированием понимают такое кодирование, при котором измерительная информация представленная в дискретной форме требует минимальное количество символов при заданной верности, т.е. отношении сигнал – шум квантования. Требование рационального кодирования сообщений обусловлены тем, обстоятельством, что в случае нерационального кодирования на первом этапе избыточность сохраняется и на последнем. В случае применения корректирующих (помехоустойчивых) кодов избыточность сообщений еще более возрастает. Процедуры рационального кодирования источника сообщений классифицируются по их возможности менять параметры или структуру кодирующего устройства для обеспечения сжатия данных. Классификация имеет вид (рисунок 7.1).
Рисунок 7.1
Фиксированная процедура имеет заданную структуру, которая остается неизменной при любых входных воздействиях. Это не позволяет оптимизировать процесс обработки данных при разных сообщениях на входах квантователя (можно оптимизировать для класса разных сообщений), но допускает простую аппаратную реализацию алгоритма. Пример фиксированной процедуры - 
-квантователь.
Параметрическая адаптивная процедура чувствительна к статистике сообщений и изменяется в соответствии с выбранным критерием свои параметры. Примерами такой процедуры являются адаптивная и разностная ИКМ.
Непараметрическая адаптивная процедура сжатия данных с изменением структуры алгоритмов сообщений является наиболее перспективной с точки зрения эффективности кодирования источника нестационарных сообщений с изменяющимися статистическими характеристиками. В этом случае меняются не только параметры, но и структура алгоритма кодирования. К таким процедурам относят алгоритм адаптивно - разностной ИКМ с перестройкой структуры фильтра – предсказателя.
7.2. Равномерное квантование мгновенных значений сигнала
Предположим, что в результате дискретизации сигнала получается последовательность непрерывных величин 
для передачи по цифровым каналам связи. Каждый отсчет необходимо проквантовать до конечного множества значений. Целесообразно разделять процесс представления последовательности множеством двоичных символов на два этапа: квантование, результатом которого является последовательность величин 
=
и кодирование, когда последовательности величин ставится в соответствие кодовое слово 
, т.е. этот процесс можно представить в виде (рисунок 7.2).
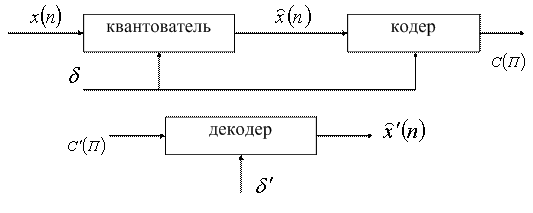
Рисунок 7.2
Обычно для кодирования квантованных отсчетов используют двоичную последовательность. С помощью B-разрядного кодового слова можно представить 
уровней квантования. Скорость передачи информации в этом случае:
, (7.1)
где 
- частота дискретизации, которая выбирается исходя из способа восстановления сигнала в приемнике, 
- число бит на отсчет сигнала.
Если - const, то единственный путь уменьшения скорости передачи состоит в сокращении числа двоичных единиц на отсчет сигнала. Определим как зависит отношение сигнал – шум квантования от разрядности кодового слова .
Рассмотрим различные способы квантования сигнала. Пусть
(7.2)
и функция плотности вероятности сигнала симметрична. Тогда
. (7.3)
Для речевого сигнала с функцией плотности вероятностей (ФПВ) Лапласа только 0,55% отсчетов сигнала окажутся вне динамического диапазона:
. (7.4)
В случае равномерного квантования:
. (7.5)
Рассмотрим характеристики равномерного квантователя в случае восьми уровневого квантования.
Первый случай. Квантователь с усечением (рисунок 7.3) имеет одинаковое количество положительных и отрицательных уровней, но нет нулевого.
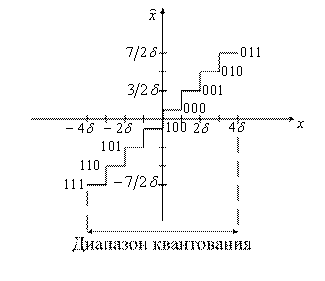
Рисунок 7.3
Второй случай. Квантователь с округлением (рисунок 7.4) имеет на один отрицательный уровень больше, но есть нулевой уровень.
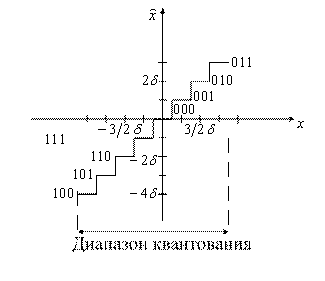
Рисунок 7.4
Для квантователя с усечением при предположении, что первый разряд знаковый, квантованное значение равно:
, (7.6)
а для квантователя с округлением:
. (7.7)
. (7.8)
Представим квантованный сигнал в виде :
(7.9)
где 
- ошибка или шум квантования, 
.
Для изучения эффектов квантования предполагают, что шум квантования обладает следующими статистическими свойствами:
- Является стационарным белым шумом.
- Некоррелирован со входным сигналом.
- Распределение шума равномерное в пределах
.
Для этой статистической модели определим отношение сигнал – шум квантования:
, (7.10)
где M – оператор усреднения.
Для B-разрядного квантователя можно записать соотношения:
. (7.11)
Тогда дисперсия шумов квантования 
при равномерном распределении ошибки равна:
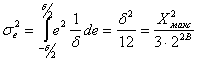. (7.12)
В случае, если 
, то получим выражение для отношения сигнал – шум квантования:
. (7.13)
Обычно отношение сигнал – шум задается в дБ:
. (7.14)
Из выражения (7.14) следует, что добавление одного разряда кодового слова улучшает отношение сигнал – шум квантования на 6 дБ. Выражение для отношения сигнал – шум квантования получено при предположении, что диапазон квантования используется полностью, если энергия сигнала изменится, то отношение сигнал – шум квантования уменьшится. В реальных условиях дисперсия телеметрического сигнала можно меняться на 20-30дБ. По этой причине для поддержания отношения сигнал – шум квантования на заданном уровне в случае равномерного квантования необходимо увеличивать число уровней квантования, при этом увеличивается избыточность сообщения. Желательно иметь устройство квантования, при котором отношение сигнал – шум квантования не зависит от уровня сигнала. Это достигается использованием неравномерного распределения уровней квантования.
7.3. Неравномерное квантование мгновенных значений
Для того чтобы относительная ошибка была постоянна при изменении дисперсии входного сигнала уровни квантования должны быть распределены по логарифмическому закону. Вместо квантования исходного сигнала можно равномерно квантовать его логарифм. В этом случае структурная схема квантователя имеет вид (рисунок 7.5).
Докажем, что в случае 
отношение сигнал – шум квантования не зависит от изменения дисперсии входного сигнала.
Выражение для квантованного логарифма входного сигнала имеет вид:
. (7.15)
Предполагается, что шумы квантования и 
независимы.
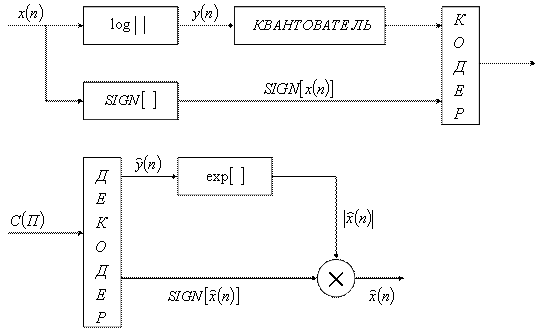
Рисунок 7.5
Тогда применяя обратное преобразование, получим:
. (7.16)
Если значение ошибки 
мало, то можно аппроксимировать экспоненту первыми членами ряда, т.е.:
(7.17)
При условии, что 
и 
независимы 
и отношение сигнал – шум равно:
. (7.18)
Следовательно, отношение сигнал - шум квантователя не зависит от мощности сигнала и зависит только от шага квантования.
Рассмотренный выше квантователь не реализуем, т.к. динамический диапазон сигнала бесконечен и требует бесконечное число уровней квантования. Для реальных случаев число уровней квантования конечно, и характеристика компрессора может быть близка к логарифмической. На практике используемые характеристики компрессора называются и А законами компандирования.
- закон компандирования имеет следующий вид:
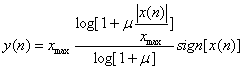. (7.19)
При малых 
и уровни квантования располагаются равномерно. При больших :
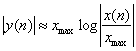(7.20)
и эта характеристика близка к логарифмической.
Можно показать, что чем выше значение параметра , тем ближе характеристика компандирования к логарифмической, но тем больше проигрыш в отношении сигнал/шум. Если дисперсия входного сигнала постоянна и известна, то неравномерный квантователь проигрывает равномерному. Экспериментальные исследования показали, что двенадцатиразрядное равномерное квантование имеет такое же отношение сигнал/шум, как и в случае восьмиразрядного квантования при - законе компандирования в случае речевого сигнала (рисунок 7.6).
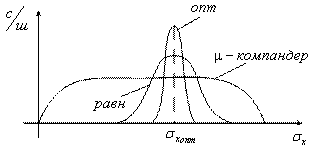
Рисунок 7.6
При 
. Отношение сигнал-шум квантования для - закона компандирования равно
(7.21)
А - закон компандирования имеет вид:
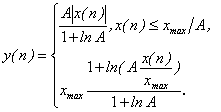(7.22)
7.4. Оптимальное квантование
Как было установлено, квантование по - закону позволяет получить постоянное отношение сигнал-шум квантователя в широком диапазоне дисперсий входного сигнала. Это достигается ценой некоторого уменьшения отношения сигнал-шум квантователя по сравнению со случаем, если диапазон квантования согласован с дисперсией входного сигнала. Когда дисперсия сигнала известна, можно так выбрать уровени и пороги квантования, чтобы минимизировать мощность шума, т.е. максимизировать отношение сигнал-шум квантователя
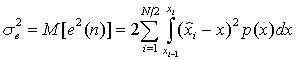, (7.23)
- ФПВ сигнала. Выражение (7.23) написано при симметричной функции плотности вероятности сигнала.
Требуется выбрать множество таких порогов и уровней квантования, чтобы минимизировать дисперсию входного сигнала. Для решения этой задачи продифференцируем 
по этим параметрам и приравняем производную к нулю
, 
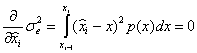(7.24)
(7.25)
При условии, что 
, 
из выражения (7.24) и (7.25) следует, что
, (7.26)
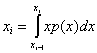. (7.27)
Т.е. оптимальные пороги равны полусумме уровней квантования, а уровни квантования есть среднее значение ФПВ сигнала на интервале 
.
Данное уравнение решается с помощью итерактивных методов для заданной ФПВ сигнала. Решение уравнения приводит к неравномерному распределению уровней квантования. Равномерное распределение уровней квантования будет только для сигналов с равномерной ФПВ. Оптимальные размеры шага квантования определены для нормального распределения, 
- распределения и распределения Лапласа.
Оптимальный квантователь дает минимум погрешности, если известна дисперсия и форма ФПВ сигнала.
Реальные сигналы обычно нестационарны. Поэтому на практике чаще используются - квантователи, несмотря на несколько меньшее отношение сигнал-шум квантователя по сравнению с оптимальными. Обычно потери составляют 3 – 6 дБ, т.е. меньше, чем один разряд квантования при известной дисперсии входного сигнала.
7.5. Адаптивное квантование
7.5.1. Вводные замечания
Из п. 7.4 ясно, что шаг квантования 
необходимо выбирать большим для согласования диапазона квантования с размахом сигнала. С другой стороны необходимо выбирать малым для уменьшения шума квантования. Одним из путей решения этой проблемы при нестационарном входном сигнале является применение - компандирования. Другой путь состоит в адаптации квантования к уровню входного сигнала. Если адаптивное квантование применяется непосредственно к отсчетам входного сигнала, то такой метод обработки называют адаптивной ИКМ (АИКМ). Известны два способа реализации АИКМ. Адаптивное квантование при первом способе состоит в том, что шаг квантования (в общем случае интервалы и уровни квантования) изменяются таким образом, чтобы соответственно изменялась дисперсия входного сигнала.
Другой способ реализации АИКМ соответствует случаю, когда характеристики квантователя не изменяются, а постоянный уровень дисперсии сигнала поддерживается за счет переменного коэффициента усиления. В обоих случаях необходимо оценивать изменяющиеся во времени характеристики сигнала.
Имеется два класса схем адаптивного квантования:
- Квантователь с адаптацией по входу, когда дисперсия входного сигнала оценивается непосредственно по этому сигналу.
- Квантователь с адаптацией по выходу, когда шаг квантования подстраивают по выходному сигналу
или кодовому слову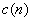 
.
7.5.2. Адаптация по входному сигналу
Рассмотрим структурную схему квантователя с переменным шагом квантования (рисунок 7.7).
Рисунок 7.7
Шаг квантования должен быть известен на приемной стороне, т.е. в этом случае отсчет описывается кодовым словом и шагом квантования. Если используется квантователь с адаптацией по входу на основе усилителя с переменным коэффициентом усиления, то квантованный сигнал описывается кодовым словом и коэффициентом усиления.
Структурная схема квантователя с переменным коэффициентом квантования приведена на следующем рисунке (рисунок 7.8).
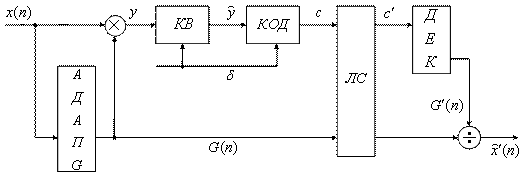
Рисунок 7.8
В системах адаптации по шагу и усилению обычно используется оценка дисперсии входного сигнала. В этом случае шаг или уровни квантования устанавливаются пропорционально СКО сигнала
, (7.28)
а коэффициент усиления - обратно пропорционально
. (7.29)
Общий подход состоит в предположении, что дисперсия входного сигнала пропорциональна кратковременной энергии. При этом дисперсия входного сигнала оценивается по формуле:
(7.30)
- импульсная характеристика фильтра нижних частот.
В интересах практической реализации устройств адаптации импульсная характеристика фильтра выбирается в виде:
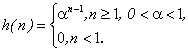(7.31)
Тогда дисперсия входного сигнала равна:
, (7.32)
(7.33)
Параметр 
импульсной характеристики фильтра определяет протяженность интервала времени, на котором сигнал вносит основной вклад в оценку дисперсии.
Обе схемы адаптивных квантователей по входу сигнала идентичны с точки зрения отношения сигнал-шум квантователя. Экспериментальные исследования в случае, если сигнал имеет ФПВ Гаусса или Лапласа показали, что адаптивное квантование дает выигрыш в отношении сигнал-шум квантователя не менее 5 - 6 дБ по сравнению с - квантователем. Если дисперсия входного сигнала изменяется в широких пределах (30 дБ и более), этот выигрыш будет увеличиваться.
7.5.3. Адаптация по выходному сигналу
Схема адаптации по выходу с переменным шагом квантования имеет вид (рисунок 7.9).
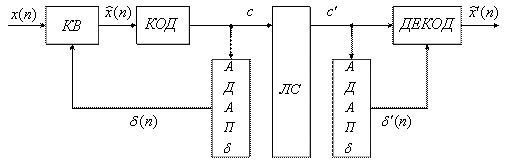
Рисунок 7.9
Системы адаптации по шагу в этой схеме цифровые. Схема адаптации по выходу с переменным коэффициентом усиления имеет вид (рисунок 7.10).
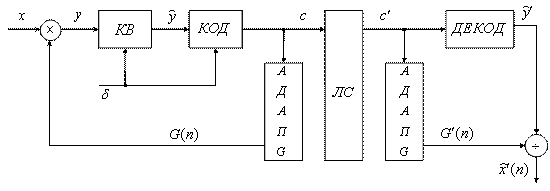
Рисунок 7.10
В обеих схемах дисперсия входного сигнала оценивается по выходному квантованному сигналу или по последовательности кодовых слов. Такие схемы обладают важным преимуществом по сравнению со схемами адаптации по входному сигналу, состоящие в том, что шаг квантования или коэффициент усиления не требуется сохранять или передавать по КС. Кроме того, система адаптации может быть реализована в цифровом виде.
Недостатком подобных квантователей является высокая чувствительность к ошибкам в кодовых словах, т.к. эти ошибки приводят не только к неправильной установке уровней квантования, но и ошибкам в шаге квантования.
Дисперсия входного сигнала в этом случае рассчитывается по формуле:
, (7.34)
где 
- квантованное значение входного сигнала, а импульсная характеристика равна:
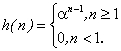(7.35)
При оценке дисперсии в схемах адаптации по входу вместо используют .
Исследования схем адаптации по выходному сигналу показали, что по сравнению с - квантователем достигается выигрыш не менее 5 дБ.
Методы адаптивного квантования дают выигрыш в отношении сигнал-шум квантователя по сравнению с квантованием по - закону при том же динамическом диапазоне сигнала. Этот выигрыш зависит от формы ФПВ входного сигнала и его динамического диапазона. В связи с этим представляет интерес рассмотрение методов разностного кодирования, которые менее чувствительны к форме ФПВ входного сигнала.
7.6. Теория разностного кодирования
Обычно между соседними отсчетами входного сигнала имеется значительная корреляция, которая слабо уменьшается по мере увеличения интервала между отсчетами. В результате разность между соседними отсчетами имеет меньшую дисперсию, чем исходный сигнал. Т.е. динамический диапазон разностного квантованного сигнала уменьшается, что позволяет при том же отношении сигнал – шум квантования уменьшить разрядность кодового слова (рисунок 7.11).
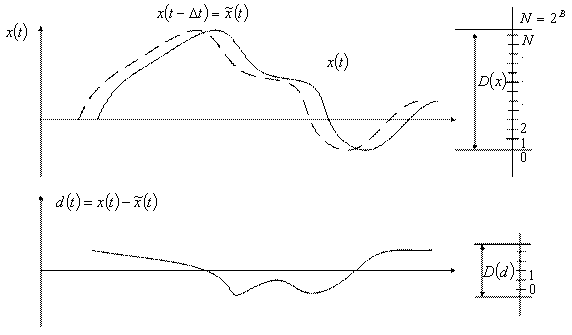
Рисунок 7.11
Рассмотрим два случая:
1. 
, т.е. кодовое слово разностного сигнала уменьшится.
2. 
. Т.е. динамический диапазон разностного сигнала расширяется до динамического диапазона исходного сигнала. Тогда длительность кодового слова исходного и разностного сигналов равны, а отношение сигнал – шум квантования разностного сигнала 
.
Рассмотрим особенности работы разностного квантователя (рисунок 7.12).
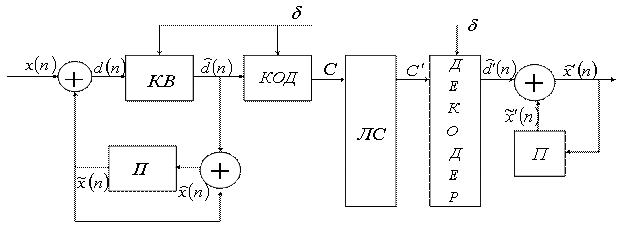
Рисунок 7.12
На входе квантователя (КВ) действует сигнал:
. (7.36)
Сигнал 
называется погрешностью предсказания или разностный сигнал. Квантованию подвергается не входной, а разностный сигнал. Квантователь может быть адаптивным или неадаптивным, равномерным или неравномерным, но во всех случаях его параметры соответствуют дисперсии погрешности предсказания. Квантованная погрешность предсказания имеет вид:
, (7.37)
где 
- ошибка квантования разностного сигнала. Из структурной схемы (7.12) следует, что квантованное значение исходного сигнала имеет вид:
. (7.38)
Тогда используя формулы (7.36 – 7.38) получаем выражение:
(7.39)
. (7.40)
Таким образом квантованный входной сигнал отличается от исходного входного сигнала на величину шума квантования разностного сигнала. Если предсказатель (П) хороший, то дисперсия разностного сигнала будет меньше дисперсии входного сигнала и квантователь с заданным количеством уровней даст меньшую погрешность при квантовании разности, чем при квантовании исходного сигнала. Отношение сигнал – шум квантования в этом случае имеет вид:
, (7.41)
где 
- отношение сигнал – шум квантователя, 
- коэффициент усиления, обусловленный разностным кодированием. Отношение сигнал – шум квантователя зависит только от свойств квантователя (равномерный, неравномерный, адаптивный) и разностного сигнала. Величина определяет выигрыш в отношении сигнал – шум при использовании разностного представления. Т.к. величина 
фиксированная, то увеличить коэффициент усиления можно только за счет минимизации 
. Для решения этой задачи определяют тип предсказателя. Рассмотрим возможность использования линейного предсказателя:
, (7.42)
где 
- порядок фильтра предсказателя, 
- коэффициенты. Дисперсия погрешности предсказателя в этом случае имеет вид:
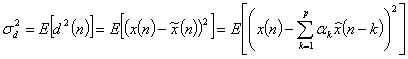. (7.43)
Дифференцируя по и приравниваем к нулю, получим систему уравнений:
(7.44)
Решением системы уравнений будут коэффициенты , при которых минимальна. В этом случае коэффициент усиления равен:
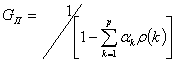, (7.45)
где 
- нормированная корреляционная функция 
. Таким образом пока 
отношение сигнал – шум квантования будет увеличиваться за счет предсказания. В случае речевого сигнала при 
получаются зависимости коэффициента усиления 
от порядка фильтра предсказателя (рисунок 7.13)
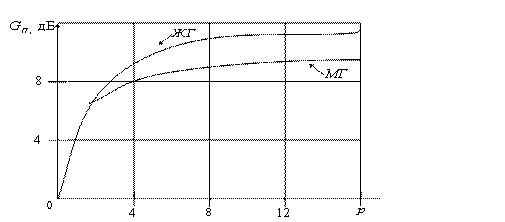
Рисунок 7.13
Даже при простом предсказателе, когда p=1, можно получить выигрыш в 6 дБ по сравнению с ИКМ, что эквивалентно добавления одного разряда в квантователь. В случае женского голоса (ЖГ) выигрыш разностного квантования выше, чем в случае мужского голоса (МГ).
Выводы:
- Разностное квантование обеспечивает выигрыш по сравнению с неадаптивным квантователем в (6 – 12) дБ.
- Величина выигрыша зависит от величины корреляции между отсчетами.
- Один и тот же предсказатель не может быть оптимальным для различных сигналов, т.к. значения коэффициентов 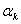зависят от вида корреляционной функции сигнала.
7.7. Дельта – модуляция
7.7.1. Общие замечания
При дельта – модуляции частота дискретизации много выше, чем частота В.А.Котельникова, 
. В результате соседние отсчеты оказываются сильно коррелированными, т.е.:
(7.46)
и можно более точно предсказать текущий отсчет по предшествующему. Т.к. в системе с дельта – модуляцией используется одноразрядный (двухуровневый) квантователь, то скорость передачи информации при этом равняется частоте дискретизации .
7.7.2. Линейная дельта – модуляция
В этом случае шаг квантования фиксирован, а порядок фильтра - предсказателя p=1. Квантователь имеет два уровня:
(7.47)
Коэффициент усиления при этом:
. (7.48)
При 
, коэффициент усиления 
, но этот результат качественный, практически же коэффициент усиления стремится к постоянному предельному значению 
.
Структурная схема системы с дельта – модуляцией имеет вид (рисунок 7.14).
Рисунок 7.14
Приемная часть схемы изображена на рисунке 7.15.
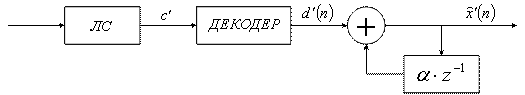
Рисунок 7.15
Рассмотрим сигналы в различных точках этой схемы (рисунок 7.16).
При дельта – модуляции в тактовых точках передается знак приращения текущего значения сигнала относительно предшествующего. При увеличении исходного сигнала формируется последовательность единиц, а при уменьшении – последовательность нулей. Квантованное значение в этом случае имеет вид:
. (7.49)
Рисунок 7.16
При 
это уравнение описывает работу дискретного интегратора, в котором осуществляется накопление шагов квантования 
.
Рассмотрим требования к характеристикам дельта – модулятора. Входной сигнал квантователя имеет вид:
, (7.50)
где - ошибка квантования.
Если пренебречь ошибкой квантования, то рассматривается как аппрокимация производной входного сигнала. Для того, чтобы последовательность отсчетов 
быстро возрастала как и последовательность отсчетов необходимо потребовать выполнение условия:
. (7.51)
Если это условие не удовлетворяется, то возникает ошибка перегрузки (пунктирная кривая на рисунке 7.16). Т.к. при перегрузке увеличение и уменьшение последовательности происходит по ступенчатой линии, то такую дельта – модуляцию называют линейной (ЛДМ).
Если в течение некоторого интервала времени входной сигнал меняется незначительно, то в линию связи поступает последовательность нулевых и единичных посылок, что приводит к флюктуациям восстановленного сигнала с размахом 
дельта, возникает шум дробления.
Рассмотрим вопрос выбора оптимального шага квантования. При большом динамическом диапазоне входного сигнала необходимо выбирать большой шаг квантования. Для точного описания малых уровней входного сигнала необходим меньший шаг квантования. Выбор шага квантования необходимо производить с условием максимизации отношения сигнал – шум квантования при заданной частоте дискретизации. Эти зависимости были исследованы для сигнала с гауссовской ФПВ и равномерным спектром. Они имеют вид (рисунок 7.17).
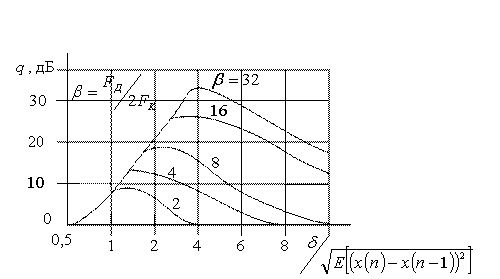
Рисунок 7.17
При некотором 
отношение сигнал – шум квантования достигает максимума. Значения левее 
соответствует перегрузке, а правее - 
- шуму дробления. Оптимальное значение отношения сигнал – шум квантования увеличивается на 9 дБ при удвоении 
, что увеличивает скорость передачи в 2 раза.
Достоинства линейной дельта – модуляции:
- Простая реализация.
- Низкие требования к синхронизации.
Недостаток линейной дельта – модуляции: грубое квантование погрешности предсказания.
7.7.3. Адаптивная дельта - модуляция
Адаптивные схемы дельта - модуляторов (АДМ) позволяют значительно улучшить характеристики ЛДМ, в частности грубое квантование погрешности предсказания. Обычно при АДМ используется адаптация по выходному сигналу. В этом случае не требуется синхронизация по кодовым словам, т.к. шаг квантования в передатчике и приемнике перестраивается в одной и той же кодовой последовательности.
Структурная схема АДМ приведена на рисунке 7.18.
Шаг квантования в этой схеме подчиняется следующему правилу:
, (7.52)
,
где - функция текущего и предшествующего кодового слова. Алгоритм выбора множителя М имеет вид
, 
- перегрузка,
, 
- шумы дробления,
.
Действительно при перегрузке последовательности на выходе состоят только из нулей или единиц, а при шуме дробления - чередующейся последовательности нулей и единиц.
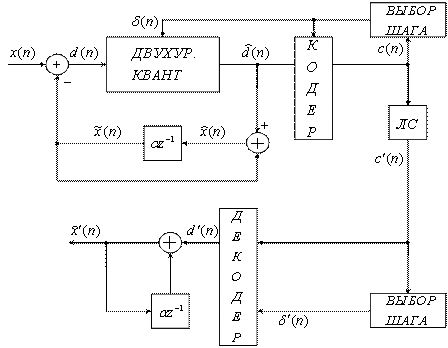
Рисунок 7.18
Исследована зависимость отношения сигнал/шум квантователя от 
(рисунок 7.19).
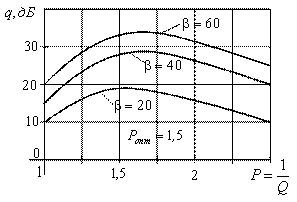
Рисунок 7.19
Сравним системы ЛДМ, АДМ и логарифмической ИКМ (рисунок 7.20) при 
и 
.
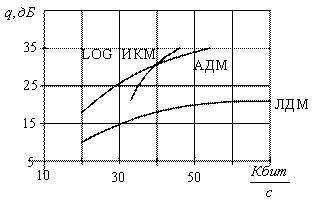
Рисунок 7.20
Проигрыш ЛДМ по сравнению с АДМ составляет 8 – 14 дБ:
т. е. 
дБ, при 
кбит/с 
, а при 
кБ/с 
.
Улучшение качества АДМ достигается путем ее незначительного усложнения, все достоинства ЛДМ при этом сохраняются. Использование предсказателя второго порядка в ЛДМ или АДМ дает выигрыш в отношении сигнал-шум квантования на 4 – 5 дБ.
7.8. Адаптивно-разностная ИКМ (АРИКМ)
7.8.1. Общие замечания
Как следует из пункта 7.6, системы с РИКМ обеспечивают выигрыш в 6 – 12 дБ по сравнению с ИКМ с - компандером. Наибольший выигрыш достигается при переходе от системы без предсказателя к предсказанию 1-го порядка. Это означает, что заданное отношение сигнал-шум квантователя системы с РИКМ можно обеспечить при разрядности меньше на 1 - 2 единицы, чем при ИКМ. Использование квантователя по - закону в разностных схемах (РИКМ) увеличивает отношение сигнал-шум еще на 6 дБ. Характеристики такой системы будут слабочувствительны к уровню входного сигнала, а общая разрядность представления уменьшится на 2 - 3 единицы. Телеметрические и речевые сигналы являются нестационарными, поэтому необходимо использовать адаптивные предсказатели и квантователи. Такие системы называются адаптивно-разностными ИКМ (АРИКМ).
7.8.2. АРИКМ с адаптивным квантованием
Рассмотрим структурную схему АРИКМ с адаптацией по выходному сигналу (рисунок 7.21).
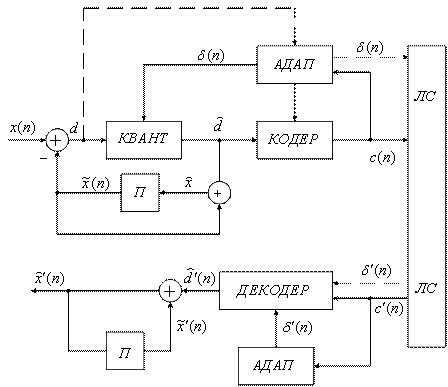
Рисунок 7.21
Систему АРИКМ с адаптивным квантованием можно построить с управлением по входу и выходу, при этом шаг квантования пропорционален среднеквадратическому значению сигнала на его входе и выходе. Можно управлять шагом квантования и по разностному сигналу. Общий выигрыш системы АРИКМ может составлять 18 – 24 дБ по сравнению с адаптивным квантователем с тем же числом уровней. Если применить - закон квантования к разностному сигналу, то выигрыш составит 24 – 30 дБ, что позволит уменьшить разрядность кодового слова на 4 – 5 единиц по сравнению с ИКМ. Дополнительным достоинством является возможность работы с входными сигналами, которые имеют большой динамический диапазон.
7.8.3. АРИКМ с адаптивным предсказателем
Все предыдущие схемы, кроме оптимальных и - квантователей принадлежат к параметрически адаптивным системам. При использовании предсказателей высокого порядка можно ожидать, что РИКМ даст выигрыш 10 – 12 дБ по сравнению с ИКМ. Величина выигрыша зависит от корреляционной формы сигнала, которая изменяется от реализации к реализации. Поэтому целесообразно использовать систему АРИКМ с адаптивным предсказанием, которая позволит дополнительно увеличить отношение сигнал-шум квантователя в случае нестационарных сигналов. При этом необходимо на блоке отсчетов определять оптимальный порядок предсказателя и коэффициенты предсказания 
. Адаптация предсказателя может осуществляться по входному или выходному сигналу.
Структурная схема системы АРИКМ с адаптивным предсказанием изображена на рисунке (рисунок 7.22).
При адаптации по входу для восстановления сигнала в приемнике необходимо передавать 
, 
и 
. Пусть коэффициент предсказания и порядок предсказания зависит от времени. При этом предсказанное значение 
имеет вид:
. (7.53)
При определении коэффициентов 
предполагают, что свойства сигнала не изменяются во времени в течение определенного интервала времени. Для речевого сигнала этот интервал составляет 50 – 100 мс.
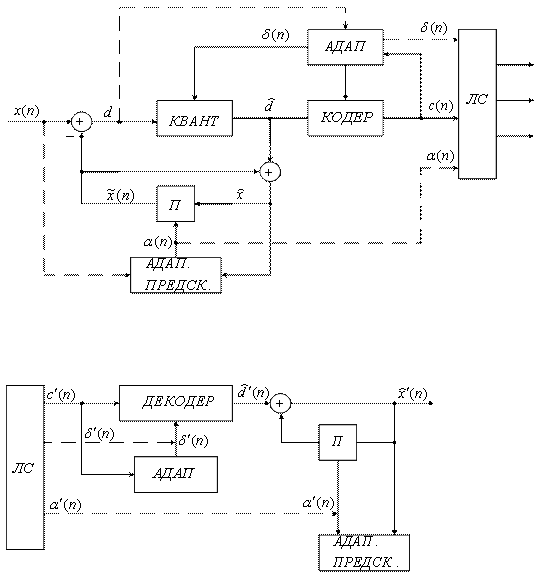
Рисунок 7.22
Рассмотрим зависимости отношения сигнал-шум для адаптивных (АП) и фиксированных (ФП) предсказаний (рисунок 7.23).
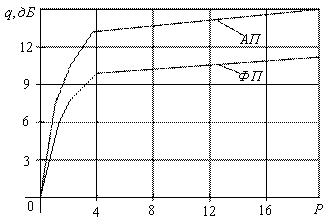
Рисунок 7.23
Верхняя граница отношения сигнал-шум при фиксированном предсказании составляет 10 дБ, а при адаптивном предсказании составляет 14 – 15 дБ. При этом чувствительность адаптивного предсказателя к изменению свойств сигнала значительно ниже, чем у фиксированного предсказателя.
7.9. Сравнение цифровых систем кодирования
Сравнение различных систем кодирования производилось при речевых сигналах [4]. Рассмотрим систему:
- Неадаптивной ИКМ с
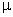- законом квантования. - Адаптивной ИКМ с оптимальным Гауссовским квантованием и управлением по входному сигналу.
- РИКМ с неадаптивным предсказателем первого порядка и адаптивным квантователем с управлением по выходному сигналу.
- АРИКМ с адаптивным предсказателем первого порядка и адаптивным квантователем с управлением по входному сигналу.
- АРИКМ с предсказателем четвертого порядка и адаптивным квантователем с управлением по входному сигналу.
- АРИКМ с предсказателем двенадцатого порядка и адаптивным квантователем с управлением по входному сигналу.
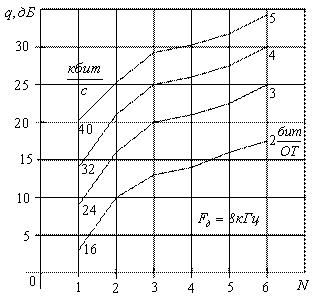
Рисунок 7.24
Кривые отстают друг от друга на 6 дБ. На практике субъективное качество речи сигнала в системе с АРИКМ оказывается лучше, чем с ИКМ при том же отношении сигнал – шум. Обычно 4-х разрядная АРИКМ с адаптивным квантованием оказывается лучше 8-ми разрядной ИКМ с - компандером. Если применять - квантователь для разностного сигнала, то выигрыш АРИКМ дополнительно увеличится на 6 дБ по сравнению с ИКМ и - законом квантования.
8. Разделение каналов в радиолинии
8.1. Вводные замечания
Для всех РТМС характерна многоканальная передача. Число уплотняемых каналов в современных РТМС достигает 100-10000. при этом применяются различные виды операций уплотнения и разделения каналов, а также различные процедуры организации этих операций. На выбор метода разделения каналов влияет:
- число уплотняемых каналов;
- скорость передачи информации;
- требования к помехоустойчивости и скрытности передаваемой информации;
- условия использования многоканальной системы;
- возможности унификации и стандартизации аппаратуры.
8.2. Классификация методов разделения каналов
Все используемые методы разделения каналов можно классифицировать на линейные и нелинейные (рисунок 8.1).
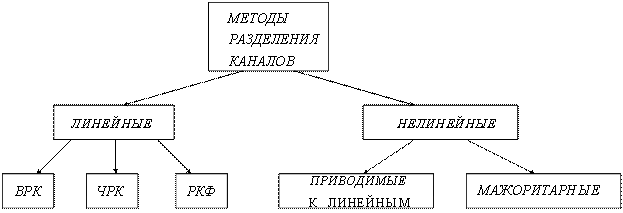
Рисунок 8.1
К линейным относятся методы, при которых операции разделения осуществляются линейными устройствами. Для осуществления линейного разделения каналов необходимо и достаточно, чтобы канальные сигналы составляли ансамбль линейно независимых сигналов. В качестве таких сигналов часто используют ансамбль ортогональных сигналов. Обычно используют следующие линейные методы разделения каналов: частотное разделение каналов - ЧРК, временное разделение каналов - ВРК, разделение каналов по форме - РКФ. Для пояснения принципа линейного разделения каналов рассмотрим структурную схему многоканальной системы (рисунок 8.2).
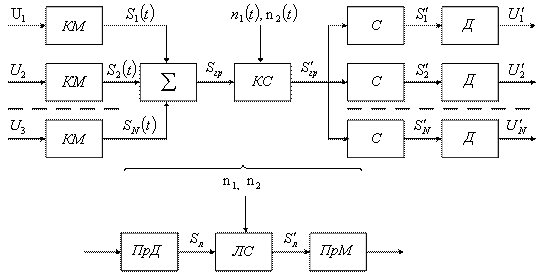
Рисунок 8.2
Первичные сигналы 
с выхода аппаратуры обработки информации АОИ поступают на канальные модуляторы (КМ), где преобразуются в канальные сигналы 
.
, (8.1)
где 
- оператор, осуществляющий взаимное однозначное преобразование.
Для образования группового сигнала все N канальных сигналов складываются:
. (8.2)
В передатчике этот сигнал преобразует в высокочастотное колебание:
, (8.3)
где M – оператор преобразования.
Передатчик (ПрД), приемник (ПрМ), линия связи (ЛС) образуют канал связи (КС). На входе приемника принимается сигнал:
, (8.4)
где 
- мультипликативные и аддитивные помехи. В приемнике (ПрМ) происходит обратное преобразование сигнала:
. (8.5)
Действие канального селектора характеризуется оператором 
. Процесс разделения каналов можно представить следующим образом:
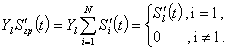. (8.6)
Т.е. l-ый селектор реагирует лишь на сигнал 
и не реагирует на сигналы других каналов. В демодуляторах (Д) происходит обратное преобразование канального сигнала в сообщение 
. Необходимым условием нормальной работы многоканальной системы является взаимное однозначное преобразование, осуществляемое операторами 
.
При ВРК канальные сигналы представляют собой последовательности прямоугольных импульсов, не пересекающихся во времени.
При ЧРК канальные сигналы представляют собой гармонические колебания с не перекрывающимися частотными спектрами.
При РКФ канальные сигналы перекрываются по времени и частоте, оставаясь ортогональными за счет их формы.
Известно большое число нелинейных методов уплотнения и разделения каналов. В некоторых случаях при нелинейном уплотнении возможно использование линейного разделения каналов. Например, если операция уплотнения состоит в перемножении канальных сигналов:
, (8.7)
причем канальные сигналы обладают тем свойством, что их логарифмы образуют ансамбль линейно независимых сигналов. То путем логарифмирования группового сигнала, т.е. его нелинейной обработкой можно привести задачу нелинейного разделения к известной задаче линейного разделения.
. (8.8)
Из нелинейных методов уплотнения в настоящее время используется логическое (мажоритарное) уплотнение, имеющее ряд достоинств по сравнению с другими методами. К достоинствам мажоритарного уплотнения относятся:
- Отсутствие буферной памяти, необходимой для согласования потока информации с пропускающей способностью канала связи.
- Отсутствие при передаче служебной (адресной) информации.
- Информационная скрытность.
8.3. Условия линейной разделимости сигналов
Для линейной разделимости каналов необходимо, чтобы с помощью оператора выполнялась следующая операция:
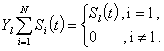(8.9)
При этом сигналы должны удовлетворять определенным условиям. Пусть 
- множество канальных сигналов к-го канала. Назовем 
- линейно разделимыми множествами, если для них справедливо выражение (8.9).
Теорема: Для того, чтобы множества были линейно разделимыми, необходимо и достаточно, чтобы они удовлетворяли условию линейной независимости. Условием линейной независимости сигналов (функций) определенных на отрезке 
является невозможность тождества:
(8.10)
при любых значениях коэффициентов 
,
,…,
, кроме случая 
. Если окажется, что можно подобрать коэффициенты ,,…,, при которых удовлетворяется соотношение (8.10), то сигналы станут линейно зависимыми и неразделимыми. К линейно независимым сигналам относятся сигналы вида:
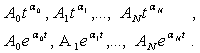(8.11)
где 
и 
- вещественные числа. В общем случае критерий линейной независимости функций , определенных на интервале дается теоремой Грама: Для того, чтобы функции были линейно независимыми, необходимо и достаточно, чтобы был отличен от нуля определитель матрицы 
, элементы которой определяются соотношением:
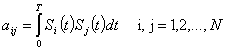. (8.12)
Т.е. условие линейной независимости функций можно записать в следующей форме:
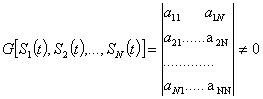, (8.13)
где G – определитель Грама. Определитель Грама всегда не равен нулю для ортогональных функций, которые удовлетворяют условию:
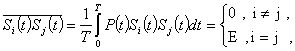(8.14)
где 
- весовая функция. Согласно теории функции действительного переменного систему линейно независимых функций можно свести к некоторой ортогональной системе функций. Использование как правило в качестве канальных сигналов системы ортогональных функций связано с тем обстоятельством, что разделение этих сигналов осуществляется без ухудшения отношения сигнал - шум.
8.4. Разделение сигнала по форме
При разделении сигналов по форме базисные функции 
должны быть линейно независимыми и ортогональными. При этом передаваемая информация заключается в амплитуде базисных функций. В случае разделения по форме канальный сигнал имеет вид:
, (8.15)
где - период канального сигнала, - отсчеты первичного сигнала.
Выражение справедливо в случае, когда информация заключена в амплитуде сигнала. В качестве базиса используются функции, удобные с точки зрения технической реализации. В частности полиномы Лежандра, Матье и др. При использовании полиномов Лежандра отдельные базисные функции равны:
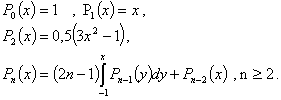(8.16)
Условие ортогональности в этом случае имеет вид:
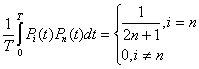(8.17)
Т.о., средняя мощность каждого ортогонального колебания равна (
). Для того чтобы выровнять мощность канальных сигналов на передающей стороне каждую базисную функцию умножают на 
.
При использовании нечетных полиномов в сигнале появляются скачки, для передачи которых потребуется широкая полоса радиоканала (рисунок 8.3).
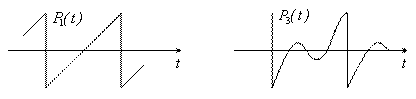
Рисунок 8.3
Для устранения этого недостатка в передаваемом сигнале у нечетных полиномов через период изменяют полярность (рисунок 8.4).
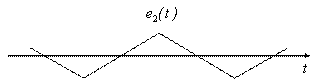
Рисунок 8.4
Рассмотрим структурную схему передающей части системы с ортогональными сигналами (рисунок 8.5).
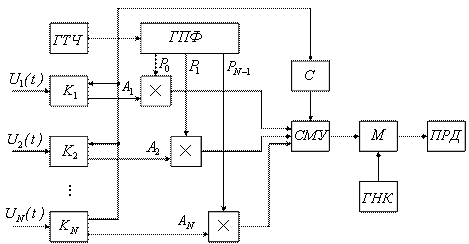
Рисунок 8.5
где СМУ – суммарно-масштабирующий усилитель, ГПФ – генератор полиномиальных функций, ГТЧ – генератор тактовой частоты, ГНК – генератор несущего колебания, К – ключ, С – синхронизатор.
Первичный сигнал 
- непрерывная функция времени. ГТЧ формирует кратковременный импульс с частотой 
. Ключ К хранит значение отсчетов за весь период, а синхронизатор формирует синхросигнал.
Тогда групповой будет сигнал представлен в следующем виде:
, 
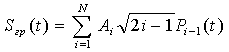, (8.18)
Для разделения канальных сигналов используют свойство их ортогональности. Эта операция сводится к вычислению скалярного произведения группового сигнала на базисную функцию выделяемого канала
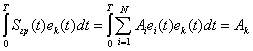(8.19)
Структурная схема приемной части системы приведена на рисунке 8.6.
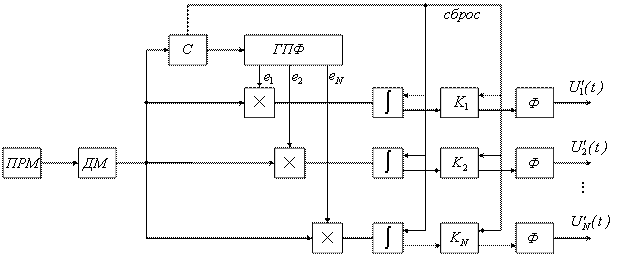
Рисунок 8.6
Ортогональные полиномы Лежандра, Чебышева и т.д. являются непрерывными аналоговыми сигналами и, следовательно, устройствам их генерирования и обработки свойственны недостатки присущие всем аналоговым устройствам:
- невозможность унификации и стандартизации большинства устройств;
- высокие требования к температурной стабильности;
- сложность технической реализации генераторов полиномиальных функций.
Поэтому в настоящее время в качестве канальных сигналов используются различные типы цифровых сигналов, в частности ансамбль функций Уолша.
8.5. Частотное разделение каналов (ЧРК)
ЧРК – частный случай разделения ортогональных сигналов. Базисные функции ортогональны в частотной области. Вид базисных функций:
, (8.20)
где 
- поднесущая частота.
Колебания (8.19) будут оставаться ортогональными при любых значениях параметров 
, и 
, если частотные спектры канальных сигналов не перекрываются.
Спектр группового сигнала показан на рисунке 8.7.
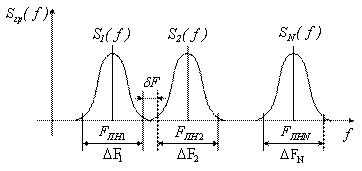
Рисунок 8.7
Для лучшего разделения каналов между спектрами канальных сигналов вводят защитный интервал 
. Общая ширина спектра группового сигнала 
:
. (8.21)
Ширина спектра зависит от вида модуляции и ширины спектра первичного сигнала.
, (8.22)
где 
- ширина спектра первичного сигнала,
- коэффициент, зависящий от вида модуляции, для амплитудной модуляции (АМ) 
.
Для частотной (ЧМ) и фазовой (ФМ) модуляции зависит от девиации частоты и индекса модуляции.
Основным недостатком системы с ЧРК является то, что с ростом числа каналов возрастает ширина спектра группового сигнала. При ЧРК сообщения можно передавать амплитудной, частотной и фазовой модуляцией. Модуляция осуществляется непрерывно при передаче всего сообщения. Обычно используют две ступени модуляции. В первой ступени каждая поднесущая может быть промодулирована по амплитуде, частоте или фазе. Возможна одновременная модуляция поднесущей по амплитуде и частоте. Эта операция удваивает число каналов без существенного расширения полосы частот тракта, но создает значительные взаимные помехи. Кроме того, можно увеличить общее число каналов, применяя однополосную модуляцию с полным подавлением одной боковой и поднесущей. Сумма модулируемых поднесущих модулирует несущую частоту передатчика по амплитуде, фазе и частоте во второй ступени модуляции. Возможны различные комбинации способов модуляции поднесущих частот и несущих колебаний:
АМ – АМ; АМ – ЧМ; ОБП – ЧМ; АМ – ОБП; ИКМ – ЧМ – ЧМ
Выбор определенного варианта построения системы с ЧРК зависти от требований к эффективности и помехоустойчивости.
Структура передающей части системы с ЧРК приведена на рисунке 8.8,
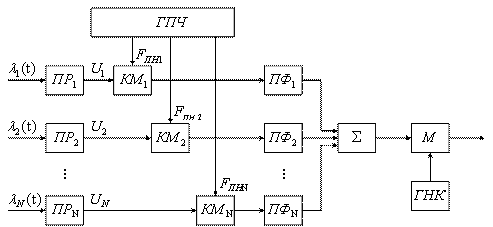
Рисунок 8.8
где ПР – преобразователь, КМ – канальный модулятор, ГНК – генератор несущего колебания, ПФ – полосовой фильтр.
Перенос спектров осуществляет КМ, а ПФ пропускают все спектральные компоненты модулированного сообщения и задерживают их гармоники. Гармоники возникают из-за нелинейности модуляционной характеристики КМ. После сумматора сигнал подается на модулятор передатчика, где происходит модуляция несущей. На первой ступени осуществляется модуляция канальных сигналов, а на второй модуляция несущей частоты. Сигнал, полученный на приемной стороне, поступает на общий демодулятор, а затем на систему из N фильтров (рисунок 8.9).
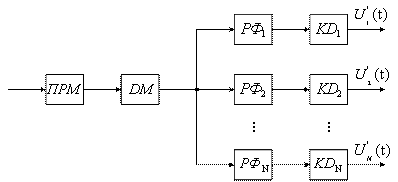
Рисунок 8.9
Амплитудно-частотные характеристики (АЧХ) фильтров аналогичны АЧХ фильтров, используемых на передающей стороне. После фильтров включены канальные демодуляторы (КД).
8.6. Временное разделение каналов
При временном разделении каналов (ВРК) сигналы, принадлежащие отдельным каналам, не перекрываются по времени. Импульс i-го канала группового сигнала 
может находиться только в i-м интервале времени (рисунок 8.10). Такие сигналы ортогональны независимо от формы импульсов, если только временное положение этих импульсов находится в пределах своего канального интервала. Частота переключения каналов выбирается так, чтобы для всех возможных реализаций сообщений удовлетворялся заданный показатель верности. Для выделения канального сигнала на приемной стороне используются базисные функции 
и 
.
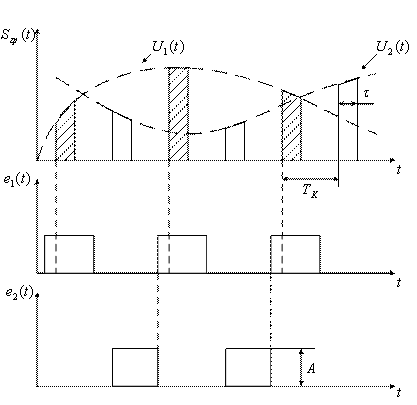
Рисунок 8.10
Такие функции ортогональны:
(8.23)
Для разделения каналов при ВРК необходимо производить следующие операции:
(8.24)
При ВРК необходима многоступенчатая модуляция, минимальное число ступеней которой равняется двум. В первой ступени какой – либо параметр периодической последовательности видеоимпульсов моделируется сообщением 
. Число канальных импульсов равняется числу каналов. Определим периодическую последовательность импульсов следующим образом:
, (8.25)
где 
- функция, характеризующая форму импульсов, 
- амплитуда импульсов,
, (8.26)
определяют начало переднего фронта k-го импульса, 
, 
- период следования импульсов, - начало отсчета последовательности, 
- сдвиг k-го импульса относительно момента времени 
, 
- длительность k-го импульса.
В первой ступени часто применяют следующие виды параметрической модуляции:
(8.27)
Возможна комбинированная модуляция, при которой одновременно меняются несколько параметров (АИМ-ШИМ, АИМ-ВИМ).
Применяют такие виды непараметрической модуляции, как КИМ,- модуляция.
Во второй ступени параметр синусоидального колебания высокой частоты модулируется суммой канальных импульсов. Обычно используется амплитудная, фазовая, частотная модуляция. В названии системы с ВРК первые буквы определяют вид модулированной последовательности импульсов, а последние – способ модуляции несущей суммы канальных импульсов (ШИМ-ЧМ, АИМ-АМ).
Рассмотрим структурную схему передающей части системы с ВРК (рисунок 8.11):
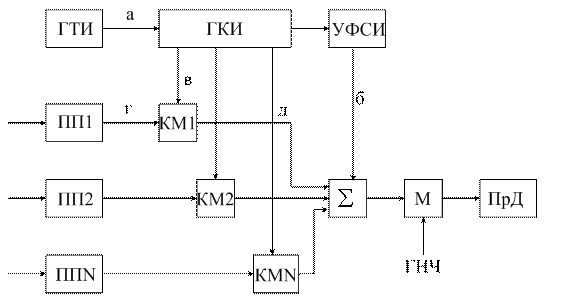
Рисунок 8.11
ГТИ вырабатывают последовательность импульсов с частотой 
. Построим эпюры в указанных точках (рисунок 8.12). Для синхронизации устройства разделения используют нулевой или канал. В устройстве формирования синхроимпульса (УФСИ) эти импульсы кодируются. Синхроимпульсы должны отличаться по форме от канального импульса. Первая ступень модуляции реализуется в канальном модуляторе (КМ), на который поступает первичный сигнал и периодическая последовательность канальных импульсов (в). Промодулированные в каждом канале импульсы складываются в сумматоре 
. Вторая ступень модуляции осуществляется в модуляторе (М) передатчика (ПрД).
Рисунок 8.12
На приемной стороне системы с ВРК принятое колебание усиливается в приемнике (ПрМ) и демодулируется (ДМ) (рисунок 8.13).
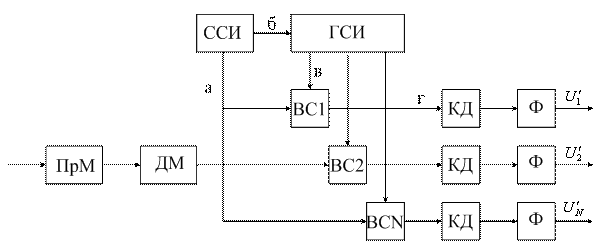
Рисунок 8.13
Далее последовательность импульсов поступает на селектор синхроимпульсов ССИ и на N-ый вход временных селекторов (ВС). Простейшая схема ССИ имеет вид (рисунок 8.14).
Рисунок 8.14
Сигнал на схему «и» подается с двух отводов линии задержки (ЛЗ). Задержка осуществляется на время 
. Сигнал со схемы ССИ используется для запуска генератора селекторных импульсов (ГСИ). Импульсы с ГСИ открывают ВСi соответствующего канала на время существования i-го канального импульса. Далее сигнал поступает на i-ый канальный демодулятор КД. Рассмотрим эпюры напряжения в различных точках схемы (8.15).
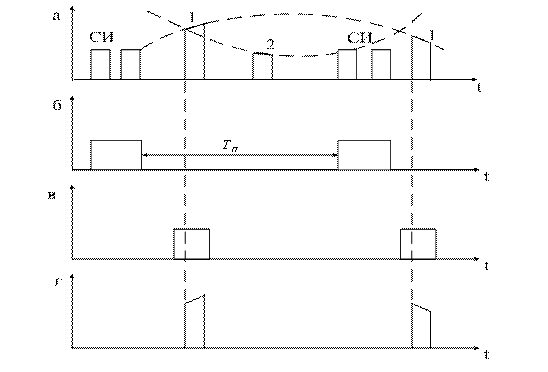
Рисунок 8.15
8.7. Мажоритарное уплотнение каналов
При мажоритарном уплотнении на входе устройства установлен АЦП. В результате такого уплотнения каждой комбинации двоичного кода с блоковой длиной N в параллельной форме, поступившей от N уплотняемых источников в устройстве уплотнения ставится в соответствие комбинация двоичного кода группового сигнала с блоковой длиной n < N , представленной в последовательном коде. При этом значение каждого двоичного символа кодируется комбинацией группового сигнала, определенного в соответствии с логической функцией абсолютного большинства, т.е. мажоритарно. Как и при ВРК нелинейность группового тракта не приводит в этом случае к появлению междуканальных помех. Кроме того двоичный код группового сигнала имеет минимально возможный пикфактор:
. (8.28)
При данном нелинейном методе уплотнения оказывается возможным линейное разделение каналов просто реализуемое на цифровом устройстве. Рассмотрим структурную схему устройств уплотнения N каналов (рисунок 8.16).
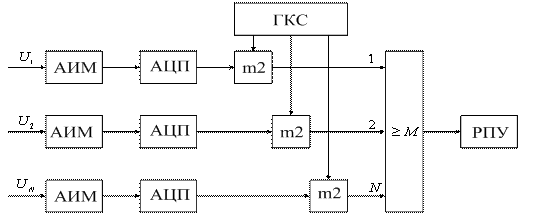
Рисунок 8.16
Моделирующие сообщения от N источников представленные двоичным кодом одновременно во всех каналах поступают на один из входов канального модулятора (КМ). В качестве КМ используется сумматор по модулю два. На другие входы КМ поступает канальный сигнал закрепленный за данным каналом. Канальный сигнал представляет собой комбинацию двоичного кода с блоковой длиной n, которая выбирается по формуле:
, (8.29)
где 
- вероятность ошибки на один информационный символ. Длительность двоичного символа канального сигнала выбирается равной 
, где T – длительность двоичного символа модулирующего сообщения (рисунок 8.17).
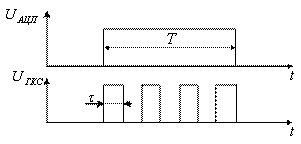
Рисунок 8.17
С выхода сумматора по модулю два в каждом канале в соответствии с операциями логического суммирования:
(8.30)
имеем или выделенный данному каналу канальный сигнал:
, (8.31)
или его инверсию:
. (8.32)
Совокупность канальных сигналов и их инверсий одновременно поступает на мажоритарный элемент. На выходе мажоритарного элемента с тактовой частотой символов канального сигнала формируется двоичное кодовое слово по следующему правилу: i-ый разряд кода (i от 1 до n) равняется единице, если число единиц поступающих на мажоритарный элемент по всем N каналам в i-ый момент времени больше или равно N/2, и равен нулю в противном случае:
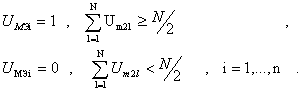(8.33)
Код, порождаемый данным кодером, будет блочным нелинейным несистематическим кодом.
Рассмотрим структурную схему устройства разделения (рисунок 8.18).
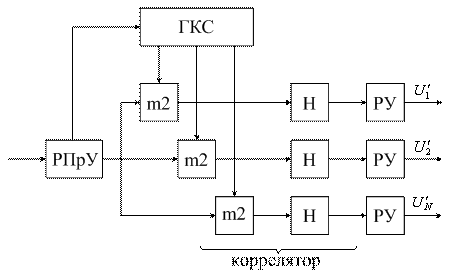
Рисунок 8.18
Устройство разделения каналов является линейным устройством. Кодированные символы группового сигнала поступают на набор из N канальных корреляторов, состоящих из сумматоров по модулю два и накопителей импульсов (Н). В качестве накопителей можно применять реверсивные счетчики. На один вход сумматора по модулю два поступают принимаемые символы группового сигнала, а на другой – символы соответствующего канального сигнала. По окончанию счета n cимволов решающее устройство определяет знак накопленной суммы. Если число единиц 
, то выносится решение о приеме информационного символа 1, и наоборот
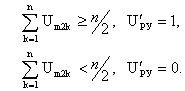(8.34)
В качестве канального сигнала обычно используются двоичные ортогональные сигналы, например функции Уолша.
Недостаток мажоритарного уплотнения: даже при отсутствии шумов в канале связи будет ошибка, обусловленная методом уплотнения.
9. Радиотелеметрические системы с временным разделением каналов
9.1. Виды модуляции, применяемые в системах с ВРК
9.1.1. Амплитудно – импульсная модуляция (АИМ)
При АИМ амплитуда импульса изменяется в соответствии с передаваемым сообщением.
, (9.1)
где 
, - амплитуда немодулированных импульсов, 
- парциальный коэффициент модуляции, 
- модулирующая функция, - функция, описывающая форму импульсов, 
.
Различают АИМ1 и АИМ2. При АИМ1 амплитуда импульса следит за изменением модулирующей функции (рисунок 9.1).
. (9.2)
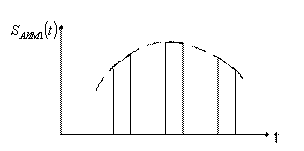
Рисунок 9.1
В случае АИМ2 амплитуда импульса определяется мгновенным значением моделирующей функции в точке 
(рисунок 9.2)
. (9.3)
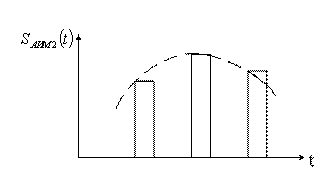
Рисунок 9.2
Анализ показывает, что АИМ2 сопровождают искажения. Обычно АИМ2 применяют на приемной стороне, если перед демодуляцией АИМ1 осуществляется удлинение импульсов, а также перед АЦП. Рассмотрим частотный спектр АИМ1 в случае:
. (9.4)
Спектр АИМ1 содержит: постоянную составляющую, составляющую на частоте модуляции, бесконечную сумму гармоник, составляющую на частотах 
(рисунок 9.3).
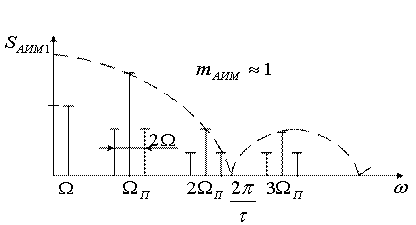
Рисунок 9.3
Особенностью спектра АИМ1 является то, что амплитуда составляющей на частоте модуляции не зависит от частоты, а амплитуды боковых составляющих при гармониках 
одинаковые.
Демодуляцию АИМ сигналов можно осуществлять с помощью полосового фильтра (ПФ) или ФНЧ. Для демодуляции с помощью ПФ на его выходе получается амплитудно-модулированные колебания, и для выделения этих сообщений требуется применение амплитудного детектора (рисунок 9.4).
Рисунок 9.4
При демодуляции с помощью ФНЧ на выходе получается непосредственно сообщение (рисунок 9.5).
Рисунок 9.5
Усилитель (У) на выходе ФНЧ необходим, т.к. амплитуда сигнала на частоте модуляции 
, 
.
Для увеличения отношения 
на выходе ВС ставят расширитель (Р) импульсов, т.е. преобразуют АИМ1 в АИМ2 (рисунок 9.6).
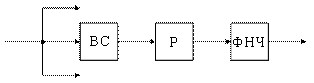
Рисунок 9.6
Такой метод демодуляции АИМ широко применяется. Спектр АИМ2 содержит те же спектральные составляющие, что и АИМ1, но имеются существенные отличия. Амплитудные составляющие на частоте 
зависят от частоты, а составляющие 
различны и так же зависят от частоты (рисунок 9.7).
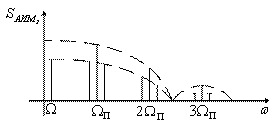
Рисунок 9.7
Из рассмотрения спектра АИМ2 следует, что использование АИМ2 приводит к неустранимым искажениям при демодуляции. Но чем меньше длительность импульсов 
, тем меньше эти искажения проявляются при демодуляции. Необходимо при расчете параметров выбирать верхнюю частоту ФНЧ из условия 
.
9.1.2. Широтно-импульсная модуляция
Параметры модуляции при ШИМ не входят явно в формулу (9.1), поэтому аналитическая запись ШИМ имеет вид:
, (9.5)
где 
и 
- функции, описывающие изменение передних и задних фронтов импульсов соответственно.
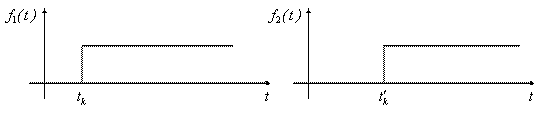
Рисунок 9.8
Закон изменения длительности импульсов имеет вид:
, (9.6)
где 
- длительность импульсов при отсутствии модуляции, 
- нормированная модулирующая функция, 
- парциальный коэффициент модуляции.
Различают двухстороннюю (ШИМ) и одностороннюю (ОШИМ) модуляцию. Кроме того, различают ШИМ первого и второго рода. В случае ШИМ1 длительность импульсов определяется значением модулирующей функции в момент возникновения передних и задних фронтов импульсов.
При ШИМ2 длительность импульсов пропорциональна мгновенным значениям модулирующего напряжения в тактовых точках. В качестве модулятора ОШИМ2 используют фантастроны. При 
различия между ШИМ1 и ШИМ2 не существенны. Выражения для ОШИМ1 и ОШИМ2 имеют вид
при ОШИМ1 
,
при ОШИМ2 
.
Определим спектр ОШИМ1 при модулирующей функции 
(рисунок 9.9).
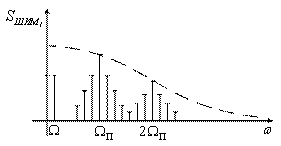
Рисунок 9.9
Спектр ОШИМ1 содержит постоянную составляющую, составляющую на частоте модуляции 
и составляющие на частотах 
. Неискаженная демодуляция ОШИМ1 вследствие наличия составляющих невозможна.
Частотный спектр ОШИМ2 имеет те же составляющие, что ОШИМ1. Отличие заключается в наличии в спектре ОШИМ2 гармоник модулирующей частоты 
, что приводит к дополнительным искажениям сигнала при демодуляции (рисунок 9.10).
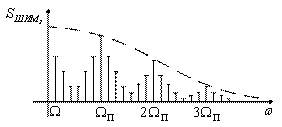
Рисунок 9.10
Практически используется способ демодуляции ШИМ и ОШИМ с помощью ФНЧ (рисунок 9.11).
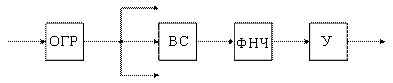
Рисунок 9.11
Обычно выбираются следующие параметры ОШИМ 
, 
. Исходя из длительности 
осуществляется выбор полосы приемного тракта.
9.1.3. Время-импульсная модуляция
При ВИМ сдвиг импульсов 
относительно тактовых точек 
изменяется по закону 
(рисунок 9.12)
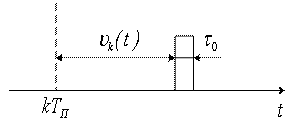
Рисунок 9.12
Для ВИМ выражения для последовательности импульсов имеет вид 
, (9.7)
где 
, 
. Различают ФИМ первого и второго рода.
Для ВИМ первого рода 
, т.е. временной сдвиг импульсов пропорционален значению модулирующей функции 
в момент появления этого же импульса.
Для ВИМ второго рода 
, т.е. временной сдвиг импульсов пропорционален значению в тактовых точках. Различия между ФИМ-1 и ФИМ2 при 
становятся несущественными.
Определим спектр ФИМ-1, полагая что (рисунок 9.13).
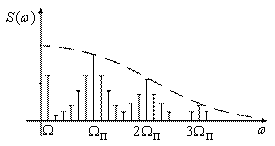
Рисунок 9.13
Спектр ФИМ-1 состоит из:
- постоянной составляющей;
- полезной составляющей на частоте ;
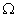- составляющих с частотой ;
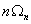- составляющих с частотами
.
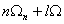Частотные составляющие спектров ШИМ-1 и ВИМ-1 совпадают, но амплитуды полезных составляющих зависят от индекса модуляции и очень малы.
Амплитуда полезной составляющей определяется выражением:
(9.8)
При 
, 
и амплитуде полезной составляющей на выходе ФНЧ в этом случае равна 
, т.е. зависит от частоты модуляции.
Следовательно, демодуляция ВИМ-1 с помощью ФНЧ сопровождается завалом нижних и подъемом верхних модулирующих частот. Демодуляция ВИМ с помощью ФНЧ на практике не используется. Чтобы уменьшить искажения и увеличить уровень полезной составляющей на выходе демодулятора при демодуляции ВИМ применяются преобразования ВИМ в ШИМ или ВИМ в АИМ.
Рассмотрим преобразование ВИМ в ОШИМ с помощью триггера (рисунок 9.14), где 
- сигнал в тактовых точках, 
- сигнал ВИМ, 
- сигнал на выходе триггера.
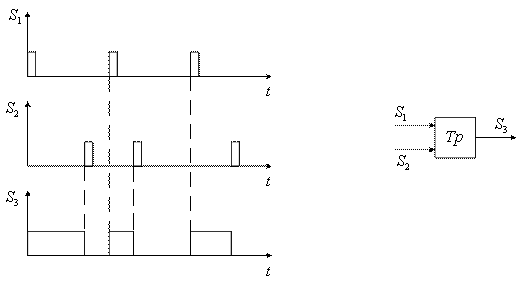
Рисунок 9.14
Преобразование ВИМ в АИМ (рисунок 9.15).
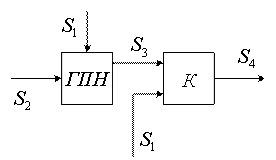
Рисунок 9.15
Рисунок 9.16
Демодулятор ВИМ имеет вид, приведенный на рисунке 9.17, где ПР – преобразователь.
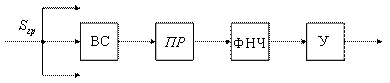
Рисунок 9.17
9.2. Переходные искажения в системах ВРК
Переходные искажения появляются в результате переходных процессов, которые сопровождаются появлением или исчезновением импульсных сигналов в многоканальных системах.
Причиной появления переходных искажений является недостаточно широкая полоса пропускания тракта радиолинии. Различают помехи первого рода, возникающие вследствие искажений спектра группового сигнала в области высоких частот (ВЧ) и помехи второго рода, возникающие из-за искажений спектра группового сигнала в области нижних частот (НЧ). Искажения первого рода возникают из-за завала ВЧ составляющих спектра в тракте радиолиний. Искажения второго рода возникают в передающей аппаратуре до модулятора несущей и в приемной (видеоусилителе) в области модулирующих частот.
9.2.1. Переходные искажения второго рода
Возникновение помех второго рода обусловлено нелинейностью АЧХ и ФЧХ видеоусилителя общего тракта в полосе, которую занимает спектр модулирующих частот. Полагаем, что на входе видеоусилителя с характеристикой 
подана последовательность импульсов n каналов, и в одном канале осуществляется АИМ (рисунок 9.18).
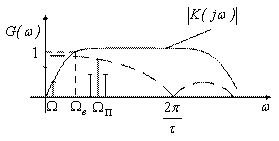
Рисунок 9.18
Нелинейность АЧХ и ФЧХ видеоусисилителя приводит к уменьшению полезной составляющей на 
, а ее фаза сдвигается на угол 
, что отображено на векторной диаграмме (рисунок 9.19).
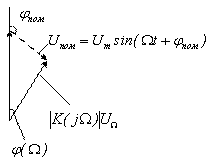
Рисунок 9.19
Из анализа векторной диаграммы следует, что в состав спектров немодулируемых последовательностей как бы вводится дополнительная составляющая на частоте с амплитудой 
и уменьшается амплитуда полезной составляющей в спектре модулируемого сигнала (рисунок 9.20).
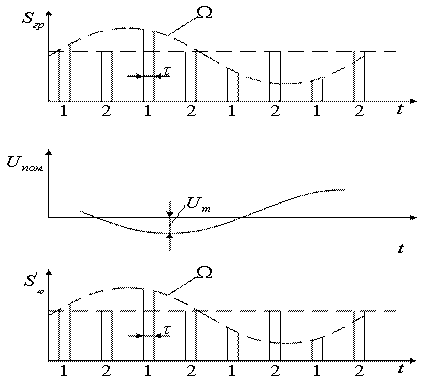
Рисунок 9.20
Сигнал на выходе i-го временного селектора без искажений имеет вид:
, (9.9)
.
Групповой сигнал при искажениях второго рода описывается выражением:
. (9.10)
Если модуляция импульсов осуществляется во всех N каналах, то из векторной диаграммы следует, что:
. (9.11)
Тогда сигнал на выходе временного селектора равен:
. (9.12)
Для демодуляции АИМ используют ФНЧ. Сигнал на выходе ФНЧ при 
равен:
. (9.13)
Оценим переходные искажения коэффициентом 
:
, (9.14)
где 
- мощность сигнала i-го канала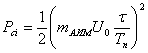 
, а мощность помехи равна:
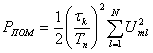. (9.15)
При условии, что коэффициенты модуляции во всех N каналах одинаковы, формула для коэффициента переходных искажений имеет вид:
. (9.16)
Если 
, а расстояние между циклами 
,то:
. (9.17)
Введем понятие среднего коэффициента искажений 
:
. (9.18)
В этом случае:
. (9.19)
Таким образом, при N >> 2 , 
. Таким образом, при увеличении N уменьшается 
и падает мощность помех 
.
Основным способом устранения НЧ искажений является применение фиксатора уровня (рисунок 9.21):
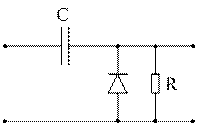
Рисунок 9.21
Постоянная времени фиксатора уровня канала связи выбирается достаточно большой, но такой величины, чтобы напряжение на емкости успевало отслеживать заваленные НЧ спектра АИМ.
Переходные помехи 2-го рода действуют сильнее на АИМ и менее на ШИМ и ВИМ. Если используются ШИМ и ВИМ, то для уменьшения помех 2-го рода применяют ограничитель.
9.2.2. Переходные искажения первого рода (в области ВЧ)
Переходные искажения первого рода проявляются как наложение импульсов друг на друга и возникают при недостаточно широкой полосе пропускания тракта или при малом временном интервале между импульсами соседних каналов (рисунок 22):
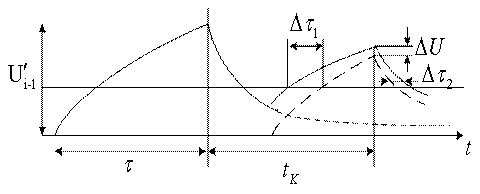
Рисунок 9.22
Для анализа переходных помех первого рода аппроксимируют ВЧ часть частотной характеристики общего тракта частотной характеристикой RC – цепи (рисунок 9.23).
Рисунок 9.23
Амплитудно – частотная характеристика RC цепи имеет вид:
, (9.20)
где 
- полоса на уровне 0.707, 
.
В случае переходные искажения 1-го рода в системе ШИМ ошибка равна:
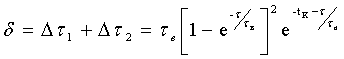. (9.21)
Т.е. для уменьшения ошибки необходимо увеличивать полосу тракта 
или интервал 
, возможноиспользовать предискажения.
9.3. Помехоустойчивость РТМС с ВРК
Флюктуационные помехи на входе приемного устройства приводят к изменению амплитуды и длительности импульсов. Помехи, действующие между импульсами называются – интервальными. Помехи, накладывающиеся на импульсы делятся на срединные и краевые. При АИМ путем стробирования приемника можно избавиться только от интервальных помех. При ВИМ и ШИМ использование ограничений по минимуму и максимуму позволяет избавиться от срединных помех, но действие краевых помех остается. Оценим помехоустойчивость РТМС с АИМ-АМ, ШИМ-ЧМ, ФИМ-АМ.
Структурная схема приемной части системы с ВРК изображена на рисунке 9.24.
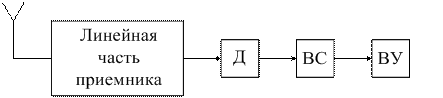
Рисунок 9.24
Полагаем, что отношение сигнал - шум достаточно велико. Шум нормальный белый в полосе приемника. В качестве критерия оценки используется отношение случайной компоненты выходного сигнала к полезной, т.е. относительную случайную ошибку. В этом случае при АИМ-АМ относительная случайная ошибка имеет вид [2]:
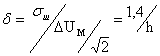, (9.22)
где 
- среднее квадратичное значение шума, 
- максимальное изменение амплитуды импульса, h – отношение сигнал - шум.
Следовательно для уменьшения относительной случайной ошибки в этом случае необходимо увеличивать отношение сигнал - шум.
При ШИМ-ЧМ относительная случайная ошибка равна:
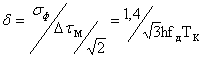, (9.23)
где 
- среднее квадратичное значение флюктуаций фронта импульсов, 
- максимальная полезная ширина импульса, 
- девиация частоты несущей, 
- канальный интервал.
Для уменьшения относительной случайной ошибки системы ШИМ-ЧМ надо увеличить отношение сигнал - шум, девиацию частоты несущей и канальный интервал.
При ФИМ-АМ относительная случайная ошибка имеет вид:
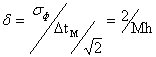, (9.24)
- максимальное временное смещение, 
– индекс временной модуляции, - длительность импульсов. Для уменьшения относительной случайной ошибки в этом случае необходимо увеличивать индекс временной модуляции и отношение сигнал – шум.
9.4. Многоступенчатая коммутация в РТМС с ВРК
Количество измеряемых величин и точность их измерения меняется в широких пределах, что требует применения разных частот дискретизации. В случае использования одного задающего генератора для увеличения гибкости аппаратуры используют многоступенчатую коммутацию, обеспечивающую разные тактовые частоты.
Принцип многоступенчатой коммутации показан на (рисунке 9.25).
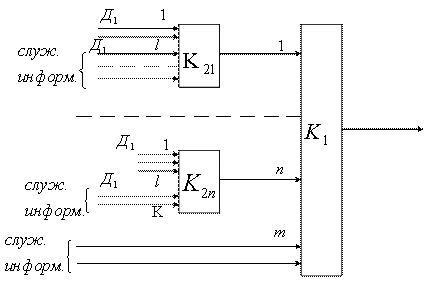
Рисунок 9.25
Первая ступень коммутаторов 
имеет m входов с временем подключения одного входа 
. Вторая ступень включает n коммутаторов с временем подключения 
. Входы с (n+1) до m используются для передачи служебной информации и осуществления синхронизации, аналоговые входы с (l+1) до К коммутаторов . Для простоты будем считать, что m=n, l=k, тогда 
, где N – общее число датчиков в схеме.
Возможны два варианта использования схемы (рисунок 9.25):
1) Все коммутаторы работают синхронно и синфазно. А 
, т.е. за время подключения одного входа коммутатора , коммутатор успевает опросить все m входов. Следовательно, на выходы схемы будут последовательно поданы сигналы всех первых датчиков, затем вторых и т.д. Увеличение частоты опроса для ряда датчиков достигается путем их подключения одновременно к нескольким входам одного коммутатора (рисунок 9.26).
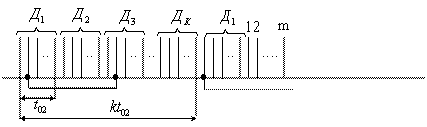
Рисунок 9.26
2) Все коммутаторы работают синхронно и синфазно, а 
. Т.е. на выходы схемы последовательно подаются сигналы всех датчиков коммутаторов 
, затем 
и т.д. Увеличение частоты опроса ряда датчиков достигается подключением датчика одновременно к нескольким одноименным клеммам разных коммутаторов второй ступени (рисунок 9.27).
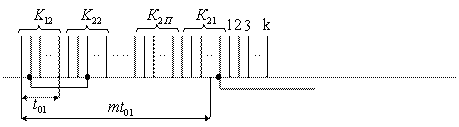
Рисунок 9.27
Возможно включение третий ступени коммутации.
9.5. Синхронизация в РТМС с ВРК
9.5.1. Системы и сигналы синхронизации
Система синхронизации в РТМС с ВРК обеспечивает синхронную и синфазную работу коммутаторов, установленных на передающей и приемной станции. Нарушение синхронизма ведет к потере информации во всех каналах. В циклических РТМС через время 
, равное периоду опроса, начинается новый цикл. Для разделения каналов необходимо обозначить начало цикла. Для этой цели перед импульсом первого канала включается специальный сигнал (начало кадра), отличающийся от остальных сигналов по амплитуде, длительности или форме (рисунок 9.28).
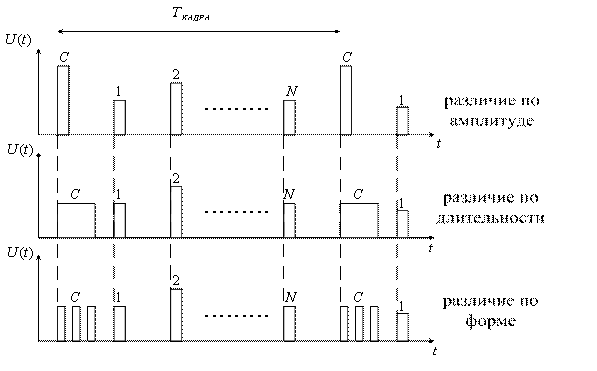
Рисунок 9.28
Такая синхронизация называется кадровой. На приемной стороне осуществляется выделение синхросигнала. Системы синхронизации могут быть двух типов: синхронные и стартстопные. Синхронные системы работают независимо от того, передается информация или нет. В этих системах предъявляются очень высокие требования к стабильности частоты генераторов.
В стартстопных системах передающий и приемный распределители работают совместно в течении одного цикла, равного длине кадра или длительности кодовой комбинации. Каждый новый цикл в них начинается с исходного синфазного положения. Рассмотрим обе системы.
Синхронная система синхронизации
В этом случае осуществляется подстройка фазы колебаний высокостабильного генератора приемной станции под фазу колебаний передающей станции. В качестве сигналов, по которым производится фазирование, могут использоваться кадровые посылки, канальные сигналы и символы кодовых комбинаций.
Типичная схема коррекции фазы генератора приемной станции изображена на рисунке 9.29.
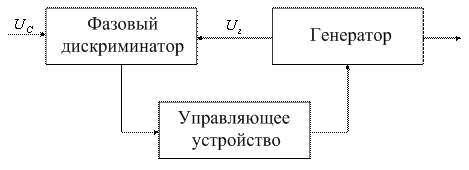
Рисунок 9.29
В фазовом дискриминаторе происходит сравнение фаз принимаемых и передаваемых импульсов, далее формируется управляющий сигнал, воздействующий на генератор.
Стартстопные системы синхронизации
Структура сигнала при стартстопной синхронизации изображена на рисунке 9.30.
Стартовая, информационные и стоповя посылки отличаются по амплитуде, длительности или форме.
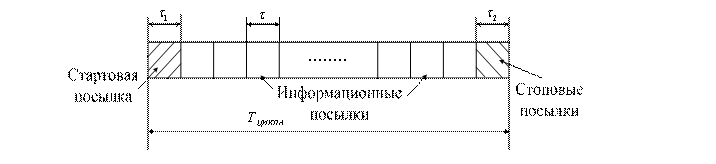
Рисунок 9.30.
При включении передатчика с помощью стартового импульса запускается синхронизатор приемного устройства. В конце цикла передачи синхронизатор останавливается стоповым импульсом. В промежутке между стартовым и стоповым импульсами передаются информационные посылки.
9.5.2. Методы кадровой синхронизации
Различают следующие методы кадровой синхронизации: маркерную, безмаркерную и инерционную.
Маркерная синхронизация осуществляется путем передачи в начале кадра синхроимпульса (маркера), отличающегося от информационных и других служебных сигналов. В приемной станции осуществляется обнаружение и выделение маркерного сигнала, из которого формируется кадровый сигнал. Структура селектора маркерного сигнала зависит от его формы. Если маркерный сигнал отличается по амплитуде от информационных импульсов, то схема селектора имеет вид (рисунок 9.31).
Рисунок 9.31
Недостатком этой схемы является невысокая помехоустойчивость.
Схема селектора маркерного сигнала, отличающегося от информационных сигналов по длительности, приведена на рисунке 9.32.
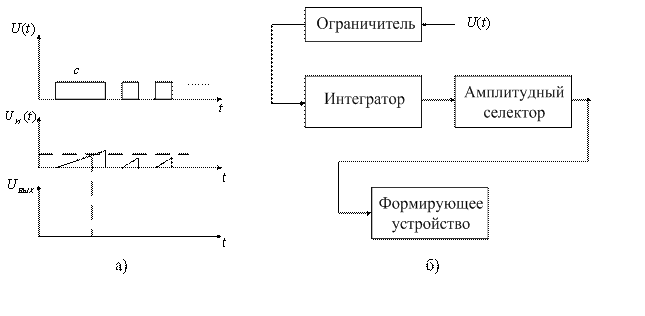
Рисунок 9.32
Данная схема обладает более высокой помехоустойчивостью, чем схема изображенная на рисунке 9.31.
Наибольшей помехоустойчивостью обладает схема селектора маркерного сигнала, отличающегося от информационных сигналов по форме (рисунок 9.33).
Безмаркерная синхронизация является частным случаем маркерной синхронизации, когда синхросигнал отсутствует. Начало кадра определяется по паузе, длительность которой равна удвоенному канальному интервалу (рисунок 9.34).
При инерционной синхронизации для управления работой слектора приемной станции используется инерционный генератор синхроимпульсов, который подстраивается по фазе принимаемыми синхросигналами.
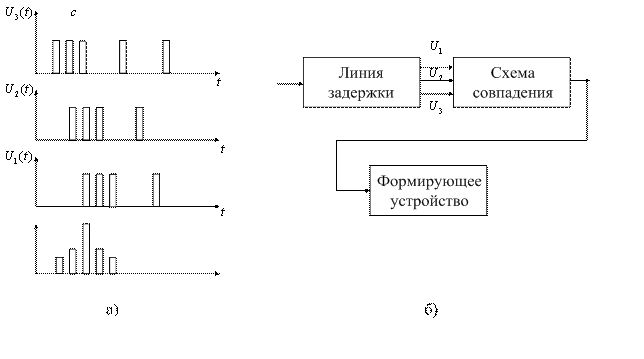
Рисунок 9.33
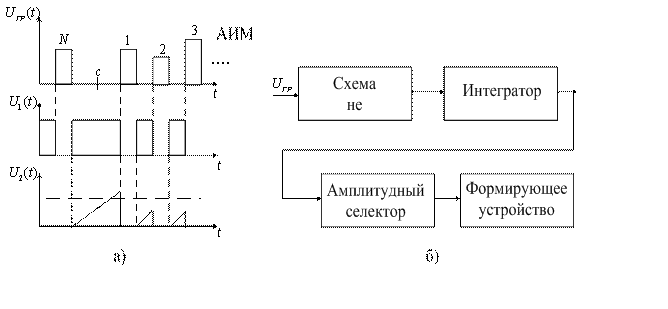
Рисунок 9.34
При инерционной синхронизации кратковременные сбои не приводят к срыву синхронизма коммутаторов приемной и передающей систем. Рассмотрим блок – схему приемной части канала инерционной синхронизации (рисунок 9.35).
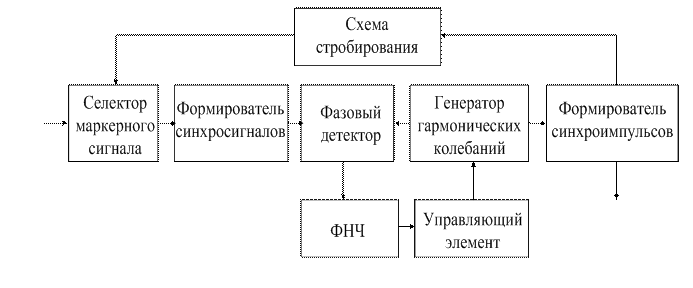
Рисунок 9.35
В селекторе осуществляется выделение маркерного сигнала по форме, амплитуде или длительности. В начальный период времени схема стробирования отключена и система осуществляет вхождение в синхронизм. Из выделенного маркерного сигнала формируется синхросигнал. Этот сигнал используется в качестве опорного, по которому производится подстройка фазы генератора. Для повышения помехоустойчивости введено стробирование маркерного сигнала.
ФНЧ обеспечивает инерционность работы схемы при пропадании сигналов синхронизации за определенное время.
10. Цифровые и адресные РТМС
10.1. Общие сведения о цифровых РТМС
Современные РТМС являются преимущественно цифровыми. Преимуществом цифровых РТМС перед другими типами РТМС является малая (менее 0,1%) погрешность передачи информации. Цифровые методы обеспечивают освобождение от помех при регенерации сигнала. В типовых РТМС с цифровой передачей преимущественно применяются двухступенчатая модуляция КИМ – ЧМ, а в космических РТМС – КИМ – ФМ и КИМ – ОФМ.
В системах, обеспечивающих высокую информативность, используется трехступенчатая модуляция КИМ – ЧМ – АМ, КИМ – ЧМ – ЧМ, КИМ – ФМ – АМ. В большинстве типовых систем применяется двоичный код с числом информационных символов в кодовой комбинации (слове) от 5 до 10. Слова дополняются вспомогательными символами, обеспечивающими их разделение на приемной стороне, а также обнаружение и исправление ошибок.
В качестве кадрового сигнала синхронизации, обеспечивающего определение начала и конца телеметрического сигнала (кадра) используются определенные кодовые комбинации, которые не применяются для передачи информации, и которые после корреляционной обработки на приемной стороне позволяют сформировать короткий импульс, обеспечивающий точную временную привязку сигнала.
Цифровые РТМС позволяют обеспечить информационную скрытность. Основной задачей при разработке цифровых РТМС является выбор типа кодера и вида модуляции, обеспечивающих минимальную полосу пропускания системы.
10.2. Функциональная схема цифровой РТМС
10.2.1. Передающая часть
Структура цифровой РТМС зависит от различных факторов: скрытности, помехоустойчивости, числа каналов, способа кодирования сообщений, системы сжатия данных, системы модуляции, методов синхронизации. Рассмотрим обобщенную функциональную схему бортовой аппаратуры цифровой РТМС (рисунок 10.1) с двухступенчатой модуляцией, здесь:
БССО – бортовые системы сбора и обработки информации;
УС – устройство сжатия;
ФС – формирователь синхросигналов;
УК – устройство калибровки;
С – синхронизатор.
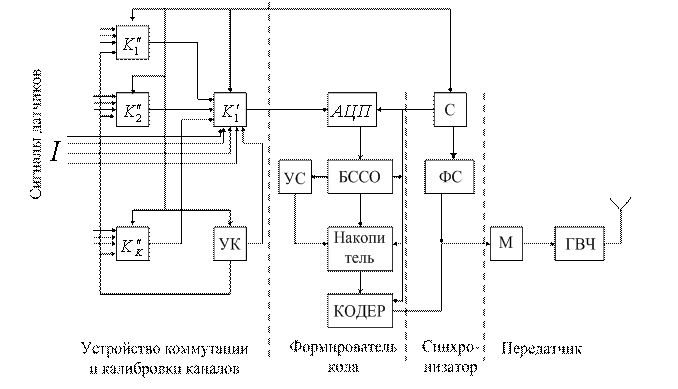
Рисунок 10.1
На схеме показана двухступенчатая коммутация каналов, причем через 
обозначен коммутатор первой ступени, а через 
- коммутаторы второй ступени. Группа обозначенная I каналов подключена непосредственно к . Такое включение обеспечивает информационную гибкость. От устройства калибровки каналов (УК) на входы подаются калибровочные сигналы, соответствующие 0 и 100% напряжения датчиков. Скорость переключения каналов и разная и определяется частотой следования импульсов, поступающих от синхронизатора (С).
Перед подачей на АЦП групповой АИМ-1 сигнал преобразуется в АИМ-2. это необходимо для того, чтобы на время кодирования значение сигнала не изменялось. АЦП должен обладать высоким быстродействием, чтобы время преобразования сигнала в цифровой код было равно или меньше длительности канального интервала. Далее сигнал в цифровой форме с выхода АЦП поступает на УС и БССО, а потом на накопитель (Н), который опрашивается с частотой переключения каналов. В накопителе с помощью сдвигающего регистра решается задача преобразования параллельного кода в последовательный. С выхода накопителя сигнал поступает на кодер, где осуществляется представление информации в избыточном коде, который используется в радиолинии.
Для увеличения быстродействия используют несколько АЦП, работающих поочередно, но при этом увеличиваются габариты аппаратуры. Например, один АЦП обслуживает четные, а другой нечетные каналы. Иногда первый АЦП обслуживает одну группу каналов, а второй другую (рисунок 10.2).
Управление работой всех блоков схемы 10.2 осуществляется синхронизатором. Сигналы с выхода кодера и формирователя сигналов синхронизации (ФСС) поступают на вход модулятора (М), управляющего работой генератора высокой частоты (ГВЧ).
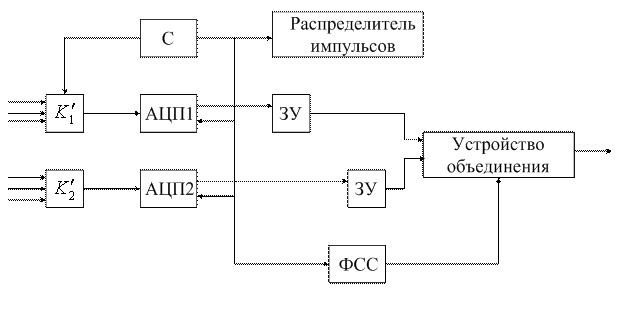
Рисунок 10.2
Возможно использование трех ступеней модуляции. Это позволяет увеличить число каналов (рисунок 10.3).
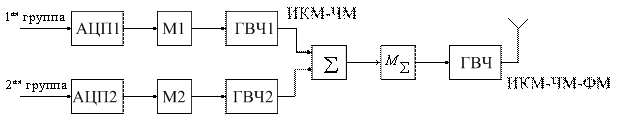
Рисунок 10.3
Сигналы первой и второй группы совпадают по времени. Частоты 
и 
ГВЧ1 и ГВЧ2 отличаются на величину ширины спектра КИМ сигнала.
Кроме того, типовая схема цифровой РТМС может включать: коммутаторы третьей ступени и устройства запоминания информации.
10.2.2. Приемная часть
Состав наземной РТМС зависит от вида модуляции сигналов, метода выделения и формирования импульсов синхронизации, способа регистрации и отображения данных телеизмерений. На рисунке 10.4 изображена обобщенная функциональная схема наземной аппаратуры с двухступенчатой модуляцией и посимвольным приемом сигналов.
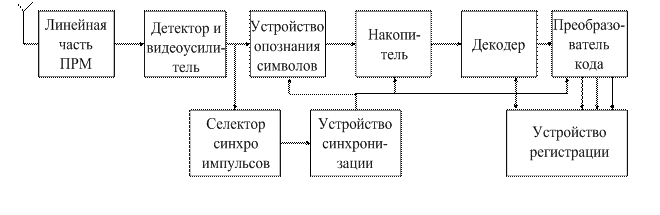
Рисунок 10.4
С выхода видеоусилителя сигнал поступает на устройство опознания символов и селектор синхроимпульсов, управляющий работой устройства синхронизации. Устройство синхронизации вырабатывает импульсы, необходимые для определения временных границ символов, слов и кадров. Устройство опознавания (или регенерации) символов определяет по выходному сигналу ПРМ, какие символы передавались. Для этого необходимы импульсы с частотой символов из УС. При передаче данных последовательным кодом символы принимаемых кодовых комбинаций запоминаются в накопителе, который управляется синхроимпульсами слов. Декодирующее устройство на основе анализа кодовой комбинации производит обнаружение и исправление ошибок. Если передача велась безызбыточным кодом, то декодирующее устройство отсутствует. Преобразователь кода осуществляет представление сигнала с выхода декодирующего устройства к виду удобному для регистрации данных.
Устойчивая работа приемной станции во многом зависит от помехоустойчивости кадровой синхронизации, синхронизации слов и символов. В современных цифровых РТМС используются три раздельные схемы для синхронизации символов, слов и кадров.
Структурная схема устройства синхронизации приведена на рисунке 10.5.
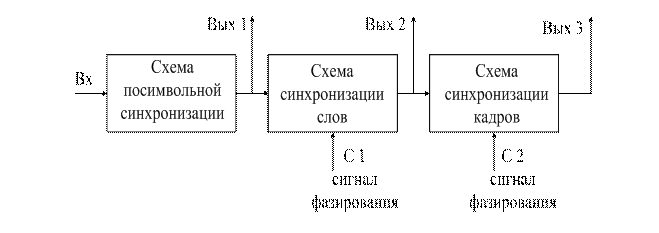
Рисунок 10.5
На вход устройства синхронизации (рисунок 10.5) поступает последовательность импульсов с селектора синхроимпульсов, которая содержит в своем спектре частоту следования символов 
. Схема синхронизации слов работает на принципе деления частоты 
, где n – число символов в кодовой комбинации. Для фазирования схемы синхронизации слов используются импульсы, выделенные селектором синхропризнаков слов. Аналогично работает схема синхронизации кадров. Коэффициент деления этой схемы 
, где N – число каналов РТМС. Для фазирования используются сигналы, выделяемые селектором маркеров кадра.
10.3. Устройство сжатия телеметрических данных
Устройство сжатия предназначено для использования на борту космического аппарата. Обслуживает 480 каналов и обеспечивает 
при использовании алгоритма сжатия на основе предсказателя нулевого порядка. Устройство выполнено на интегральных микросхемах. Схема включения представлена на рисунке 10.6.
Рисунок 10.6
Устройство сжатия приведенное на рисунке 10.7 содержит:
1. Справочное ЗУ – в нем хранится последний существенный отсчет для каждого информационного канала, пределы допуска (апертура) и знак приоритета. Когда на вход компаратора от АЦП поступает новая выборка данных, то из справочного ЗУ производится считывание последней переданной величины, пределов допуска и других сведений.
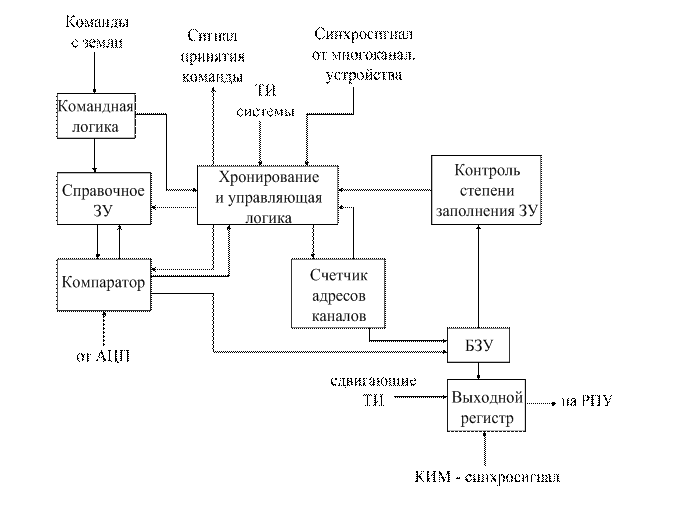
Рисунок 10.7
2. Компаратор – осуществляет операцию 
и сравнивает d и 
(допуск апертуры). Если 
, то выборка вводится в справочное ЗУ, а также в буферное запоминающее устройство (БЗУ) и передается в РПУ.
3. БЗУ – используется для временного запоминания существенных выборок, поступающих с непостоянной скоростью и преобразования их в поток данных с постоянной частотой следования.
4. Схемы хронирования и управления – вырабатывают сигналы, необходимые для управления устройства сжатия данных. Для хронирования используются тактовые импульсы (ТИ) системы и синхросигнал многоканального устройства (СИ). Упраляющая логика позволяет изменять пределы допуска (апертуру), принимать или отбрасывать существенные выборки в соответствии с сигналами от компаратора и схемы контроля степени заполнения БЗУ, а также по сигналам командной логики.
5. Счетчик адресов каналов – необходим для обращения к справочному ЗУ и для выдачи адреса при вводе данных в БЗУ.
6. Выходной регистр – преобразует данные из параллельной формы в последовательную. Скорость считывания задается тактовыми импульсами. Сигналы, передаваемые по линии связи содержат адресную информацию о принадлежности к определенному каналу, информацию о времени задержки, а также синхросигналы. Синхросигналы водятся в выходной регистр.
7. Система приоритета в Управляющей Логике включается при переполнении БЗУ. При этом в первую очередь ухудшается качество передачи данных с низшим приоритетом (увеличивают ). Если БЗУ очищается, то уменьшают в первую очередь наиболее важных каналов. Изменение характеристик устройства сжатия осуществляется как автоматически, так и по командам с земли.
8. Командная логика управляет вводом для каждого канала начальных пределов допусков, знаков приоритета и распределением информации в справочном ЗУ по командам с земли и по программе.
10.4. Классификация БССО
Классификация БССО приведена на рисунке 10.8.
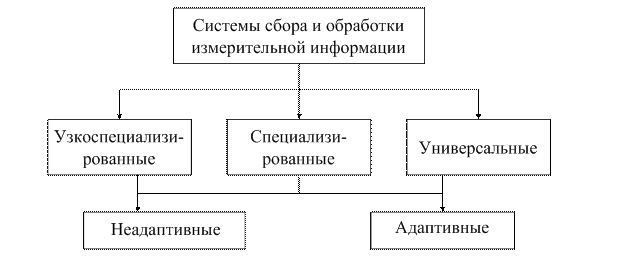
Рисунок 10.8
Узкоспециализированные БССО предназначены для выполнения небольшого числа функций:
- Сбора и регистрации данных.
- Подготовки данных для передачи по каналам связи.
- Вывод на индикацию.
Специализированные БССО выполняют следующие функции:
- Изменение программы сбора данных.
- Анализ и отображение наиболее существенной части измерительной информации.
- Определение состояния технических систем.
- Сжатие и передача данных.
Универсальные БССО решают задачи обработки данных с одновременным управлением штатного оборудования ЛА. Строятся на базе мультипроцессорной техники.
В соответствии с возможностью адаптации к изменениям условий функционирования (характеристик потоков измерительной информации) БССО делят на два класса: неадаптивных и адаптивных.
Неадаптивные системы изменяют свои характеристики по сигналам с пункта управления.
Адаптивные - самостоятельно изменяют свои характеристики. Это необходимо, когда законы распределения потоков входной информации неизвестны.
Узкоспециализированные БССО
Функции таких БССО несложны, поэтому можно обойтись без использования ЭВМ. Для таких систем характерен жесткий алгоритм функционирования этапов: 1-сбора, 2-регистрации, 3-подготовки для передачи, 4-индикации.
Первая система разработана французской фирмой S FIM в начале 50-х годов. В США в 1952г. принят закон о использовании таких систем (черных ящиков) на всех самолетах гражданской авиации. Обязательно регистрируются на магнитную ленту четыре параметра, характеризующих трассу полета: 1-скорость, 2-высота, 3-вертикальное ускорение, 4-курс.
В настоящее время число регистрируемых параметров ЛА более 20-30. в качестве регистраторов используются магнитофоны и ЭВМ.
Примером подобной системы есть БССО самолета (Дуглас) ДС-10, которая используется с 1970г (рисунок 10.9), где 1 – управление скоростью регистрации, 2 – метки времени, 3 – цифровые данные.
Все датчики разбиты на две группы высокого и низкого уровня. Подсистема нормировки состоит из двух блоков, каждый принимает 160 аналоговых сигналов.
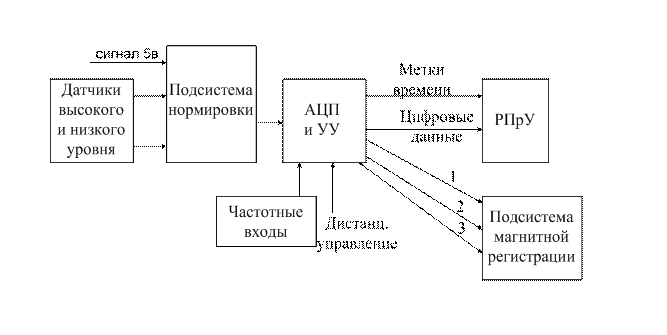
Рисунок 10.9
Производится нормировка к уровню 
5в. АЦП осуществляет опрос 320 нормированных каналов, а также 10 ЧМ сигналов о ВЧ вибрациях.
Подсистема регистрации производит запись последовательным ИКМ кодом данных на магнитную ленту. Максимальная скорость регистрации 5000 бит/с при плотности записи на магнитный носитель 330 бит/мм.
Дистанционное управление используется для изменения режимов работы и скорости регистрации. Аналогичные системы использовались в американских спутниках в 1970 годах.
Специализированные БССО
В состав специализированных БССО вводится БЦВМ. Задачи БЦВМ :
- Техническая диагностика неисправностей.
- Адаптивный опрос и сжатие измеряемой информации.
- Определение спектральных характеристик.
- Определение статистических характеристик.
- Рациональное кодирование.
- Определение летно – технических характеристик.
Применяются с 1963г. вместе с возникновением ЭВМ третьего поколения (на интегральных схемах). Впервые специализированные БССО использовались в военной авиации для решения сложных баллистических задач, связанных с применением ракет.
Фирма IBM впервые установила специализированные БССО с параметрами 500 тыс. операций в секунду и объемом памяти 32000 26-ти разрядных слов на космическом аппарате. Mariner – 4.
Примером специализированных БССО является система, установленная на самолете С-5А. Эта система может работать на ракетах и КЛА (рисунок 10.10).
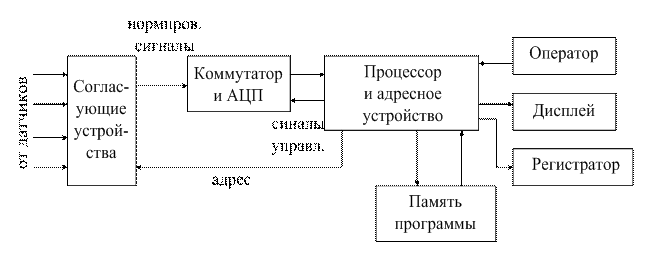
Рисунок 10.10
Данные от 20 блоков, включающие 
1000 датчиков подаются на СУ. Сигналы нормируются по амплитуде и через коммутатор, а также АЦП проходят в БЭВМ, где кодируются, анализируются на наличие отказов и обрабатываются. Результаты анализа выводятся на дисплей и на панель управления и индикации. При нормальном полете используется одна частота опроса, при возникновении дефекта для детального анализа частота может регулироваться сигналом управления. Кроме того может регулироваться и порядок опроса (команда «адрес»). На экране дисплея можно вызвать сигналы любой подсистемы и сравнить с эталонами. Программа работа задана жестко и не обладает адаптивностью.
Универсальные БССО
Появление универсальных БССО связано с тем, что:
- Допустимое время для принятия решения уменьшается.
- Стоимость расхода горючего увеличивается.
- Любая ошибка дорого обходится.
Т.е. время на обработку и управление КЛА и ЛА резко сократилось. БЭВМ, установленные на универсальных БССО, решают задачи:
- диагностики;
- регистрации и обработки данных;
- управление режимом работы.
Для этой цели разработаны мультипроцессорные многофункциональные системы магистрального типа.
Во всех разработанных для КЛА универсальных БССО используется магистрально – модульный принцип построения (рисунок 10.11).
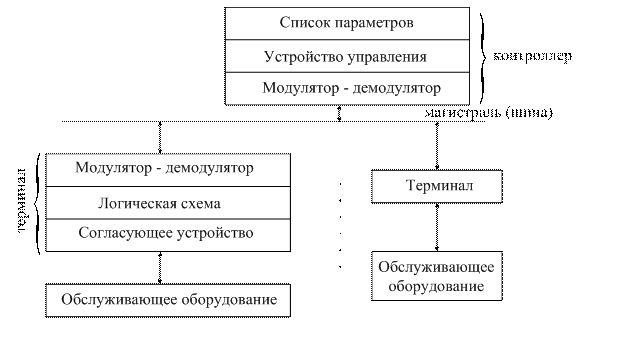
Рисунок 10.11
Терминал включает модем, логическое устройство, согласующее устройство. В модеме осуществляется модуляция и демодуляция сигналов. Логическое устройство производит предварительный анализ информации, а согласующее устройство – нормировку по амплитуде.
По сигналам программного устройства в соответствии со списком параметров производится обмен информацией между терминами и контроллером. Каждый терминал имеет свой адрес. Контроллер осуществляет обработку информации, поступившей от терминала, и задает порядок функционирования обслуживаемого оборудования. Формат данных, передаваемых между контроллером и терминалом изображен на рисунке 10.12.
От контроллера
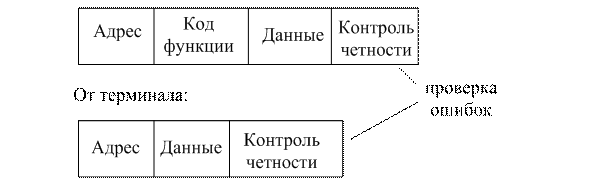
Рисунок 10.12
10.5. Адресные РТМС
К числу недостатков многоканальных систем с ВРК следует отнести:
- высокие требования к синхронизации;
- возможность только поочередной и циклической передачи канальных сигналов.
Принцип адресного разделения каналов заключается в том, что элемент сигнала каждого канала наделяется дополнительным признаком, характерным только для этого канала (рисунок 10.1), где А, И – адресная и информационная части канала.
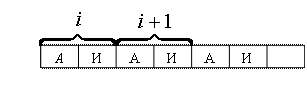
Рисунок 10.1
Наличие адреса позволяет:
- избавиться от обязательной очередности передачи данных в порядке номеров каналов;
- использовать принцип приоритета при передаче более важной информации;
- использовать систему синхронизации.
Передача многоканального сообщения при адресном разделении каналов может быть последовательной и параллельной во времени. Адресный метод позволяет создавать адаптивные РТМС. Практически используются адресные РТМС с ВРК. Недостатки адресных РТМС:
- По сравнению с цифровыми РТМС адресные РТМС имеют меньшее число каналов за счет введения дополнительной адресной информации.
- Несмотря на упрощение системы синхронизации, структура адресных РТМС сложнее структуры РТМС с ВРК. Это объясняется введением ряда дополнительных устройств в адресные РТМС.
Адресные телеметрические системы могут быть аналоговыми и цифровыми. В аналоговых системах канальный сигнал состоит из адресной и информационной части или же только из адресной части, параметры которого меняются в соответствии с изменением сигнала датчика (рисунок 10.2).
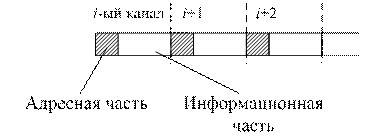
Рисунок 10.2
Упрощенные блок-схемы передающих частей адресных РТМС приведены на рисунках 10.3 и 10.4.
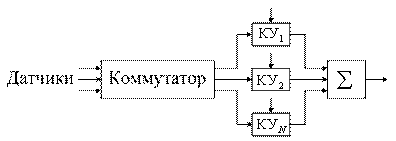
Рисунок 10.3
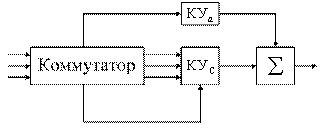
Рисунок 10.4
На первом рисунке для каждого канала имеется отдельное кодирующее устройство (КУ), которое вырабатывает как адресную, так и информационную часть кода. На втором рисунке для всех каналов имеются общие кодирующие устройства сигналов (КУс) и адресов (КУа).
В цифровых адресных РТМС как адрес, так и информационная часть канального сигнала представляется в кодовой форме.
В адресных РТМС всегда вводится дополнительная адресная информация, т.к. поток отсчетов на выходе устройства сокращения избыточности является в общем случае неравномерным. Роль преобразователя неравномерного потока в равномерный с постоянными интервалами между отсчетами обычно выполняет буферное запоминающее устройство (БЗУ).
В БЗУ часть отсчетов на какое-то время задерживается, при этом величина задержки меняется от отсчета к отсчету.
Изменение цикличности выдачи отсчетов требует введения дополнительной служебной информации о времени измерения и принадлежности отсчета (адреса). Каждый отсчет адаптивной системы состоит из трех частей (рисунок 10.5):
- кодовой группы адреса
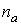; - кодовой группы времени
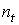; - кодовой группы, несущей информацию о значении данного параметра
.
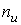Рисунок 10.5
11. Радиотелеметрическая система с ЧРК
11.1. Виды модуляции, применяемые в системах с ЧРК
11.1.1. Линейная амплитудная модуляция
Модулированное гармоническое колебание при амплитудной модуляции (АМ) в этом случае можно представить в виде
, (11.1)
где 
- коэффициент, характеризующий чувствительность модулятора; 
- модулирующее колебание; 
- частота и начальная фаза несущего колебания.
Зависимость 
от называется модуляционной характеристикой при АМ. Как известно, модулирующее колебание можно выразить с любой степенью точности рядом Фурье с конечным числом членов:
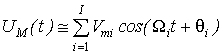. (11.2)
Тогда, выражение (11.1) можно привести к виду
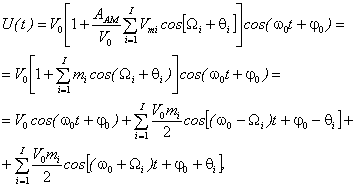(11.3)
где 
- парциальный коэффициент амплитудной модуляции, соответствующий i-ой компоненте модулирующего колебания .
Типичный вид спектра АМ колебаний изображен на рисунке 11.1
Свойства АМ колебания:
- Спектр колебания при линейной АМ всегда симметричен.
- Ширина спектра при АМ равна удвоенной гармоничной частоте модулирующего колебания
.
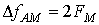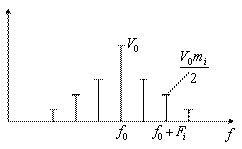
Рисунок 11.1
Определим среднюю удельную мощность АМ колебаний.
. (11.4)
Из выражения (11.4) следует, что удельная мощность одной боковой полосы спектра АМ
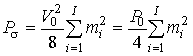. (11.5)
Т.к.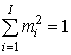 
, то, следовательно, средняя мощность равна
. (11.6)
Следовательно, АМ передатчик в режиме передачи обеспечивает увеличение средней мощности по сравнению с режимом молчания не более, чем в полтора раза. Для эффективного использования мощности передатчика используют однополосную модуляцию (ОБП), что позволяет сузить полосу пропускания приемника и увеличить мощность, расходуемую на создание одной боковой полосы. Для этого на приемной стороне необходимо с высокой точностью восстановить несущую частоту (
). ОБП широко используется в УКВ диапазоне при передаче телевизионных изображений и в телефонных системах уплотнения.
11.1.2. Линейная фазовая модуляция
Модулированное гармоническое колебание в этом случае имеет следующий вид:
, (11.7)
где 
- коэффициент, характеризующий чувствительность модулятора при ФМ. Учитывая выражение (11.2) представим (11.7) следующим образом:
, (11.8)
где 
- парциальный индекс фазовой модуляции для составляющей с частотой 
. Зависимость 
от называется модуляционной характеристикой при ФМ.
Определим спектр ФМ колебания, используя результаты теории функций Бесселя (рисунок 11.2):
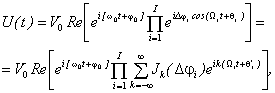(11.9)
где 
и 
.
Если 
, то
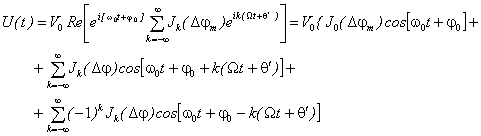(11.10)
где 
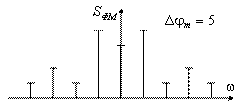
Рисунок 11.2
Спектр ФМ колебания содержит бесконечное число дискретных составляющих даже при модуляции одним гармоническим колебанием. На уровне 0,01 от амплитуды немодулированной несущей ширина спектра ФМ колебания равна
, (11.11)
где 
. Можно показать, что средняя удельная мощность ФМ колебания равна 
, т.е. мощности несущей в отсутствие модуляции.
11.1.3. Линейная частотная модуляция
Модулированное гармоническое колебание в этом случае имеет следующий вид:
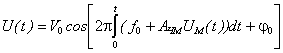, (11.12)
где 
- коэффициент, характеризующий свойства модулятора при ЧМ. Представим выражение (11.12)следующим образом:
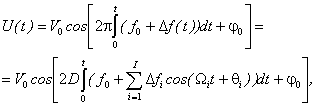(11.13)
где 
- парциальная девиация частоты за счет составляющей модулирующего колебания с частотой 
. Зависимость 
от 
называется модуляционной характеристикой при ЧМ. Учитывая, что фаза и частота связаны соотношением
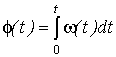(11.14)
получим
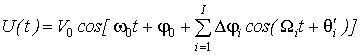, (11.15)
где 
, 
. Т.е. спектры ЧМ и ФМ колебаний совпадают, если под индексом модуляции понимать .
11.2. Характеристики группового тракта
Групповым трактом является часть РТМ системы, по которой проходит групповой сигнал (с выхода сумматора до разделителя) (рисунок 11.3)
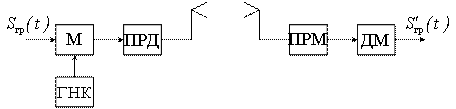
Рисунок 11.3
Групповой тракт описывается:
- амплитудной характеристикой
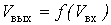; - амплитудно-частотной характеристикой;
- фазо-частотной характеристикой.
Наибольшее влияние на качество передачи информации имеет амплитудная характеристика (АХ). Нелинейность АХ вызывает появление дополнительных спектральных составляющих и как следствие межканальных помех. Для получения неискаженной модуляции во второй ступени необходимо, чтобы групповой сигнал не превышал определенного уровня (рисунок 11.4).
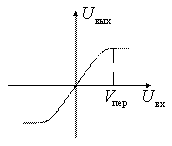
Рисунок 11.4
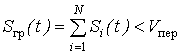, (11.16)
где 
- число каналов, 
- амплитуда модулированного колебания i-ой поднесущей.
Определим вероятность того, что групповой сигнал 
превысит уровень 
. Полагаем, что фазы всех поднесущих независимы и распределены равновероятно на интервале 
. При 
, в силу центральной предельной теоремы, распределение 
хорошо описывается нормальным законом (рисунок 11.5)
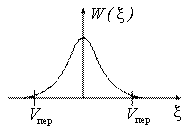
Рисунок 11.5
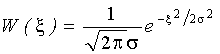, (11.17)
где 
- дисперсия процесса . Дисперсия процесса при амплитудной модуляции поднесущих с 
, как следует из формулы (11.4), равна
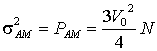. (11.18)
В случае частотной модуляции поднесущих дисперсия равна
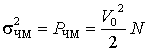. (11.19)
Определим вероятность перегрузки
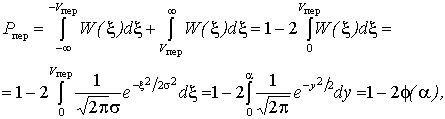(11.20)
где 
- интервал вероятностей (функция Лапласа), 
, 
.
Для РТМ систем общего назначения в случае перегрузки с вероятностью 
(
).
Тогда задаваясь уровнем 
определим уровни поднесущих колебаний в случае АМ
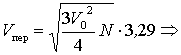
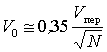, (11.21)
и в случае ЧМ
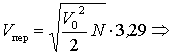
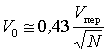. (11.22)
11.3. Причины появления искажений в ТМ системах с ЧРК
11.3.1. Вводные замечания
В РТМ системах с ЧРК возможны следующие виды искажений передаваемых сообщений:
- искажения, появляющиеся из-за внутренних флюктуационных шумов;
- переходные (линейные) искажения;
- перекрестные (нелинейные) искажения.
Линейные искажения при попадании в полосу пропускания одного канала сигналов соседних каналов. Они обусловлены недостаточной селективностью реальных полосовых канальных фильтров.
Нелинейные искажения возникают из-за наличия нелинейных элементов в групповом тракте и образования при этом множества комбинационных частот.
11.3.2. Переходные искажения (линейные)
Сложение полезного сигнала с помехой в виде части сигналов соседних каналов приводит к его искажению (рисунок 11.6).
Рисунок 11.6
Оценим влияние только одного (n-1) канала. Полагаем, что модуляция поднесущих отсутствует и начальные фазы сигналов в k-м и (k-1)-м каналах 
. Тогда напряжение в k-м канале равно
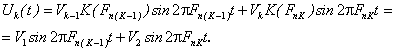(11.23)
Определим ошибку, вызванную переходными искажениями, при условии, что регистрация сигнала осуществляется безынерционными приборами.
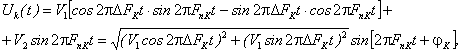(11.24)
где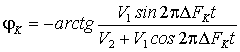 
. Тогда относительная ошибка равна
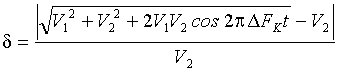. (11.25)
Из выражения (11.25) следует, что даже при передаче по k-му каналу только постоянной составляющей возможны переходные искажения. Эти искажения зависят от полосы пропускания k-ого канала и разноса частот 
.
Рассмотрим влияние инерционности регистратора на величину переходных искажений. Огибающая сигнала k-ого канала за период 
имеет вид
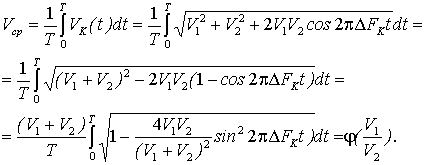(11.26)
Выражение (11.26) представляет собой эллиптический интеграл второго рода. Относительная ошибка в этом случае равна
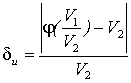. (11.27)
Зависимости относительных ошибок 
и 
от величины 
приведены на рисунке 11.7.
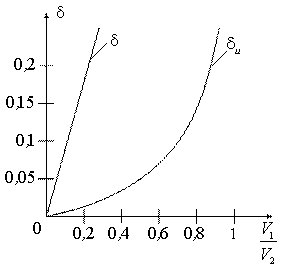
Рисунок 11.7
Т.о., инерционная регистрация позволяет уменьшить влияние переходных искажений. Анализ влияния нескольких каналов встречает значительные трудности.
При выборе характеристик фильтра и значений поднесущих частот необходимо учитывать граничную частоту сигнала, глубину и вид модуляции, величину переходных искажений.
11.3.3. Перекрестные искажения (нелинейные)
Полагаем флюктуационные шумы отсутствующими. Перекрестные искажения разделяются на низкочастотной и высокочастотной части тракта. К низкочастотной части тракта относят модулятор и демодулятор, к высокочастотной – радиотракты ПРД и ПРМ, а также пространство распространения радиоволн.
Если полоса пропускания тракта симметричны относительно несущей частоты, то как можно показать, причиной искажений при АМ во второй ступени является только нелинейность амплитудных характеристик тракта. Если приемник не настроен на частоту несущей сигнала, то нелинейные искажения возникают также за счет АЧХ и ФЧХ.
При ЧМ во второй ступени, кроме искажений вызванных нелинейностью амплитудной характеристики, основное влияние на уровень искажений оказывает фазовая характеристика.
Паразитные изменения амплитуды ЧМ сигнала устраняются ограничителем.
Нелинейность ФЧХ при ЧМ сигнале приводит к различию между мгновенными значениями частот на входе и выходе высокочастотной части тракта.
11.3.3.1. Перекрестные искажения в низкочастотной части группового тракта
Полагаем, что высокочастотная часть тракта искажений не вносит.
Перекрестные искажения в низкочастотной части группового тракта определяются нелинейностью модуляционной и демодуляционной характеристик. Эти искажения проявляются как при АМ, так и при ЧМ во второй ступени.
Для анализа перекрестных искажений аппроксимируем АХ степенным полиномом
, (11.28)
где 
- постоянные коэффициенты, 
- передаваемое и принимаемое многоканальное сообщение.
При анализе обычно ограничиваются тремя первыми членами выражения (11.28). Представим групповое сообщение в виде
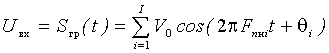, (11.29)
где 
- амплитуда поднесущей, 
- поднесущая частота i-ого канала. Подставляя (11.29) в (11.28) получим
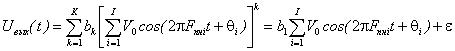, (11.30)
где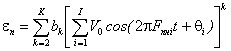 
- перекрестная помеха. Используя формулы тригонометрии можно представить выражение для перекрестной помехи в виде суммы гармонических составляющих. В таблице 11.1 приведены значения спектральных составляющих помехи.
Выводы:
1. В системах ЧРК с однополосной модуляцией в первой ступени, при том же числе каналов, уровень помех меньше, чем в системах с АМ, т.к. поднесущие отсутствуют.
2. Часть составляющих на выход группового тракта не пройдет.
3. Составляющие четвертого типа не влияют на РТМС с ЧМ, т.к. увеличение составляющих на частотах устраняется ограничителем при демодуляции.
4. В полосу группового тракта не попадают постоянные составляющие.
5. При расчетах необходимо учесть 
вторых и 
третьих гармоник, а также половину комбинационных составляющих шестого и седьмого типа.
Таблица 11.1
|
Номер составляющей |
Причина появления |
Частота |
Число составляющих |
||
|
Общее число |
На выходе группового передатчика |
||||
| 1. Постоянная составляющая |
b2 |
|
|
|
|
| 2. Вторая гармоника |
b2 |
|
|
|
|
| 3. Комбинационная составляющая |
b2 |
|
 |
|
|
| 4. Паразитическая составляющая |
b3 |
|
|
0 при ЧМ |
|
| 5. Третья гармоника |
b3 |
|
|
|
|
| 6. Комбинационная составляющая |
b3 |
|
2I(I-1) |
|
|
| 7. Комбинационная составляющая |
b3 |
|
|
|
|
6. Составляющие, возникающие из-за члена 
, дают практически равномерный спектр в полосе группового тракта со спектральной плотностью
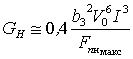. (11.31)
7. Для получения малого уровня перекрестных помех необходимо, чтобы
а) 
,
б) уменьшить уровень (применяя ОБП),
в) увеличивать 
.
11.3.3.2. Перекрестные искажения в высокочастотной части группового тракта
Полагаем, что низкочастотная часть тракта искажений не вносит. Рассматривается случай ЧМ во второй ступени. Пусть на вход ПРМ поступает ЧМ сигнал.
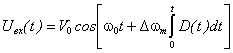. (11.32)
Тогда сигнал на выходе тракта имеет вид
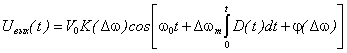, (11.33)
где 
- АЧХ тракта, 
- ФЧХ тракта.
В соответствии с выражениями (11.32), (11.33) мгновенные значения частот ЧМ сигналов на входе и выходе тракта равны
, (11.34)
, (11.35)
где 
и 
- фазы ЧМ сигналов на входе и выходе тракта. Если представить ФЧХ в виде полинома
, (11.36)
то частотная погрешность
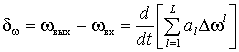. (11.37)
Обычно достаточно 
.
При линейной ФЧХ в спектре напряжения на выходе демодулятора не появляются новые составляющие. Таким образом, напряжение перекрестных помех на выходе общего демодулятора ЧМ равно при
, (11.38)
где 
- коэффициент передачи частотного детектора.
Определим спектральную плотность помехи 
, полагая, что модуляция поднесущих отсутствует
. (11.39)
Подставляя (11.39) в (11.38) получим
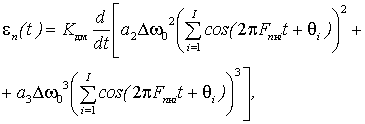(11.40)
где 
. Выражение в квадратных скобках аналогично выражению для перекрестной помехи в низкочастотной части тракта.
Из теории преобразования Фурье известно, что если две функции связаны выражением
, (11.41)
то их спектральные плотности связаны соотношением
. (11.42)
С учетом соотношений (11.42) и (11.31) спектральная плотность перекрестных помех, возникающих из-за нелинейности ФЧХ, имеет вид
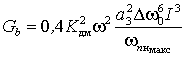. (11.43)
Из формулы (11.43) следует, что спектральная плотность таких помех имеет квадратичную зависимость от частоты, поэтому влияние перекрестных помех сказывается сильнее на каналы с более высокими поднесущими.
Во многих случаях искажениями из-за нелинейности ФЧХ можно пренебречь по сравнению с искажениями из-за нелинейности АХ группового тракта.
11.4. Выбор поднесущих частот. Телеметрические стандарты
Если число каналов мало (
), модно подобрать значение поднесущих частот 
таким образом, чтобы продукты нелинейности не попадали в полосы каналов, а располагались между ними. Среди систем с ЧРК наибольшее распространение получили системы ЧМ-ЧМ. Системы ЧМ-ЧМ обычно используются в тех случаях, когда необходимо получить следующие характеристики:
- точность выше (
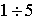) %; - ширину полосы передаваемой информации (
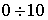) кГц; - число каналов меньше 25.
Т.е. они находят применение, когда требуется передать информацию со средней точностью и с достаточно широкой полосой при небольшом числе каналов.
Применительно к системам ЧМ-ЧМ разработаны стандарты. При 
используются следующие значения поднесущих
Гц, 
Гц, 
Гц, 
Гц, 
Гц, 
Гц.
Обычно в системах ЧМ-ЧМ необходимо, чтобы относительная девиация частоты равнялась 7,5%, т.е. 
%.
При большем числе каналов все труднее обеспечить отсутствие перекрестных помех. Поэтому при 
значения поднесущих выбирают таким образом, чтобы обеспечить минимум помех. Значения таких поднесущих являются стандартными. В настоящее время на практике используются два вида стандартов. Для первого из них характерна неравномерная шкала поднесущих частот, интервалы между которыми возрастают с увеличением номера канала. При этом полосы частот пропускания каналов оказываются различными. Поднесущие с номерами 1 – 21 обеспечивают передачу параметров с максимальной частотой модуляции от 6 до 2500 Гц. Поднесущие А, В, …Н (восемь поднесущих) обеспечивают передачу более широкополосных сигналов. РТМ системы, использующие первый стандарт, относятся к системам ЧМ-ЧМ с пропорциональной полосой. Для этих систем поднесущие частоты определяются по формуле
, (11.49)
где 
- постоянный коэффициент, 
Гц.
Данный стандарт применяют, когда требуется передать информацию как о медленно, так и о быстро изменяющихся параметрах. Если требуется передать значительное количество однотипных параметров, с одинаковыми граничными частотами, то используется второй стандарт (таблица 11.3). Здесь интервал между поднесущими принят постоянным и равным 6,7 кГц, а девиация частоты в каждом канале принята 
кГц для двадцати двух поднесущих или 
кГц для одиннадцати поднесущих частот. Т.о., для данного стандарта выбор поднесущей частоты осуществляется по формуле
, (11.45)
где 
кГц, 
кГц.
В случае системы АМ-АМ выбор поднесущих частот производится с учетом следующих факторов:
- допустимого уровня переходных помех;
- нестабильности частоты генераторов поднесущих частот;
- нестабильности настройки фильтров.
Учет влияния указанных факторов приводит к увеличению разноса поднесущих частот на 
%.
Таким образом, величина поднесущей частоты k-ого канала
. (11.47)
Радиосистемы передачи информации. Список литературы
1. Радиотехнические методы передачи информации: Учебное пособие для вузов / В.А.Борисов, В.В.Калмыков, Я.М.Ковальчук и др.; Под ред. В.В.Калмыкова. М.: Радио и связь. 1990. 304с.
2. Системы радиосвязи: Учебник для вузов / Н.И.Калашников, Э.И.Крупицкий, И.Л.Дороднов, В.И.Носов; Под ред. Н.И.Калашникова. М.: Радио и связь. 1988. 352с.
3. Тепляков И.М., Рощин Б.В., Фомин А.И., Вейцель В.А. Радиосистемы передачи информации: Учебное пособие для вузов / М.: Радио и связь. 1982. 264с.
4. Кириллов С.Н., Стукалов Д.Н. Цифровые системы обработки речевых сигналов. Учебное пособие. Рязань. РГРТА, 1995. 80с.
5. Кириллов С.Н., Бакке А.В. Оптимизация сигналов в радиотехнических системах. Учебное пособие. Рязань. РГРТА, 1997. 80с.
6. Кириллов С.Н., Шелудяков А.С. Методы спектральной обработки речевых сигналов. Учебное пособие. Рязань. РГРТА, 1997. 80с.
7. Кириллов С.Н., Бодров О.А., Макаров Д.А. Стандарты и сигналы средств подвижной радиосвязи. Учебное пособие. Рязань. РГРТА, 1999. 80с.
8. Кириллов С.Н., Малинин Д.Ю. Теоретические основы асинхронного маскирования речевых сигналов. Учебное пособие. Рязань. РГРТА, 2000. 80с.
9. Кириллов С.Н., Зорин С.В. Вейвлет – анализ случайных процессов в радиотехнических устройствах. Учебное пособие. Рязань. РГРТА, 2002. 80с.
10. Кириллов С.Н., Шустиков О.Е. Обобщенный спектральный анализ случайных процессов в радиотехнических устройствах обработки речевых сигналов. Учебное пособие. Рязань. РГРТА, 2003. 84с.
11. Кириллов С.Н., Поспелов А.В. Дискретные сигналы в радиотехнических системах. Учебное пособие. Рязань. РГРТА, 2003. 60с.
12. Кириллов С.Н., Виноградов О.Л., Лоцманов А.А. Алгоритмы адаптации цифровых фильтров в радиотехнических устройствах. Учебное пособие. Рязань. РГРТА, 2004. 80с.
13. Кириллов С.Н., Дмитриев В.Т. Алгоритмы защиты речевой информации в телекоммуникационных системах. Учебное пособие с грифом УМО. Рязань. РГРТА, 2005. 128с.