14.5.1. Проверка подлинности подписи с использованием криптосистемы с открытым ключом
14.5.2. Односторонняя функция с «лазейкой»
14.5.5. Криптосистема с открытым ключом, основанная на «лазейке» в рюкзаке
Понятие систем с открытыми ключами было введено в 1976 году Диффи (Diffie) и Хэллманом (Hellman) [12]. В общепринятых криптосистемах алгоритм шифрования может быть обнаружен, поскольку защищенность системы зависит от сохранности ключа. Один и тот же ключ применяется как для шифрования, так и для дешифрования. Криптосистемы с открытыми ключами используют два разных ключа: один — для шифрования, другой — для дешифрования. В таких криптосистемах общедоступными (без потери защищенности системы) могут быть не только алгоритм шифрования, но и ключ, применяемый для шифрования. Фактически это общедоступный каталог, подобный телефонному каталогу, который содержит ключи шифрования всех абонентов. Держатся в секрете только ключи дешифрования. Пример такой системы приведен на рис. 14.17. Перечислим важные особенности криптосистемы с открытым ключом.
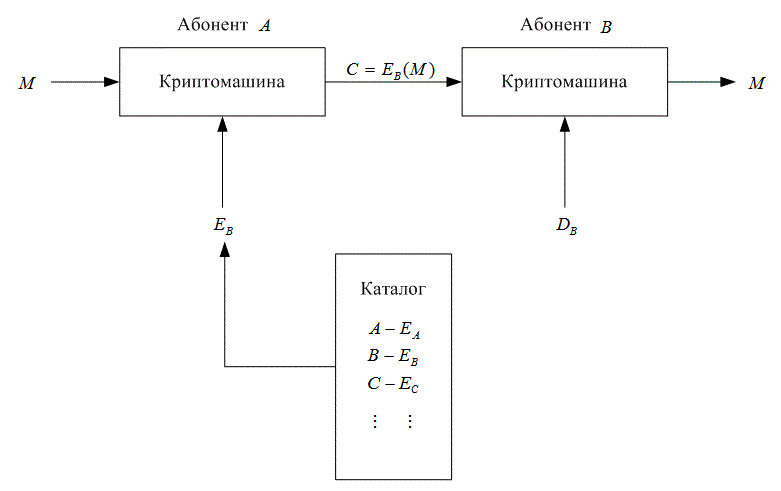
Рис. 14.17. Криптосистема с открытым ключом
1. Алгоритм шифрования ЕK и алгоритм дешифрования DK являются обратимыми преобразованиями открытого текста M или шифрованного текста С, определяемыми ключом К.
2. Для каждого ключа К алгоритмы ЕK и DK легко вычисляемы.
3. Для каждого ключа К определение DK из ЕK вычислительно трудноосуществимо.
Такая система обычно способна обеспечивать защищенность переговоров между пользователями, которые никогда ранее не встречались или не общались. Например, как показано на рис. 14.17, пользователь А может послать сообщение пользователю В, найдя ключ шифрования пользователя В в каталоге и используя алгоритм шифрования ЕB. Получив таким образом шифрованный текст С = ЕB(М), он передает его через общедоступный канал. Пользователь В - это единственный человек, который может дешифровать сообщение С, чтобы в результате получилось M = DB(C), с помощью своего алгоритма дешифрования DB.
14.5.1. Проверка подлинности подписи с использованием криптосистемы с открытым ключом
На рис. 14.18 изображено применение криптосистемы с открытым ключом для проверки подлинности подписи. Пользователь А «подписывает» свое сообщение, используя свой алгоритм дешифрования DA, что дает S=DA(M) = =EA-1(M). Затем для шифрования S он воспользуется алгоритмом шифрования ЕВпользователя В и в результате получит сообщение С=ЕВ(S) = ЕB[ЕА-1(М)], которое он передает через общедоступный канал. Когда пользователь В получает сообщение С, он сначала дешифрует его с помощью собственного алгоритма дешифрования DB, что дает DB(C) = ЕА-1(М). Затем он использует алгоритм шифрования пользователя А, в результате чего получает ЕА [EA-1(M)] =М.
Если в результате получается вразумительное сообщение, оно точно было послано пользователем А, поскольку больше никто не знает секретного кода шифрования пользователя А, с помощью которого выполняется преобразование S = DA(M). Отметим, что сообщение S зависит и от сообщения, и от подписи, а это означает, что не только В может быть уверен, что сообщения действительно приходят от А, но и А уверен, что никто, кроме В, не сможет прочесть это сообщение.
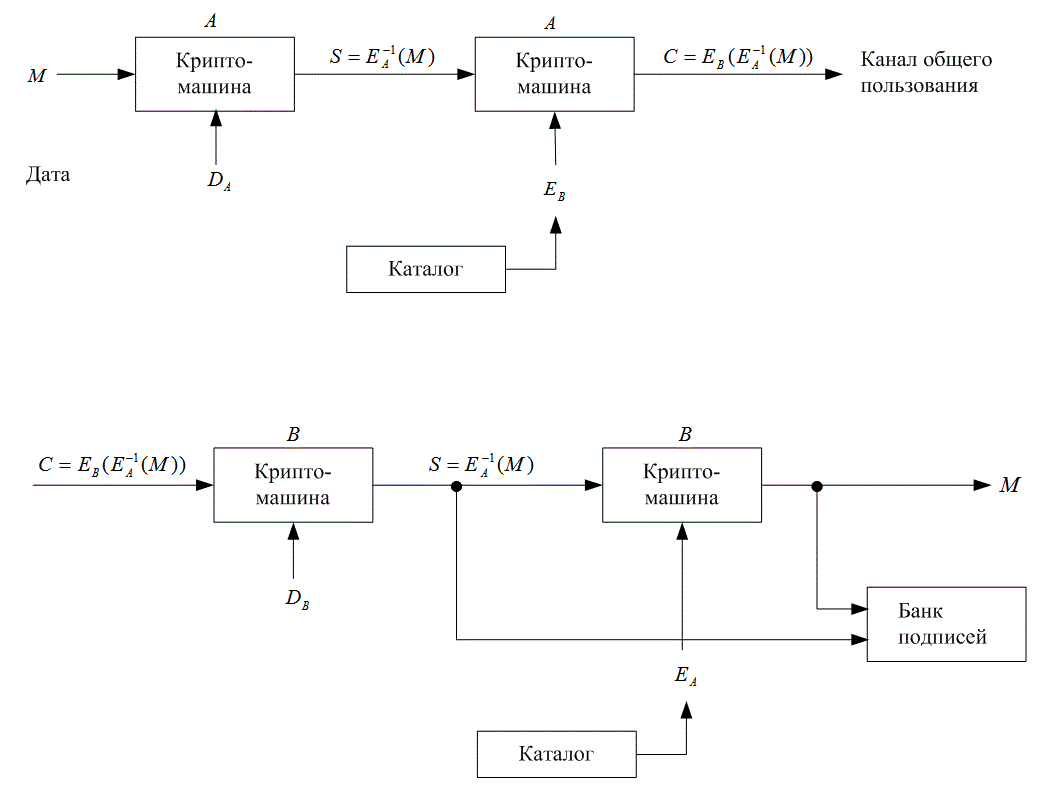
Рис. 14.18. Проверка подлинности подписи с использованием криптосистемы с открытым ключом
14.5.2. Односторонняя функция с «лазейкой»
Криптосистемы с открытым ключом основаны на понятии односторонних функций с «лазейками». Определим одностороннюю функцию как легко вычисляемую, для которой невозможно вычислить обратную. Рассмотрим, например, функцию у = х5+ 12х3 + 107х + 123. Должно быть очевидно, что при данном х легко вычислить у, но при данном у относительно сложно вычислить х. Односторонняя функция с «лазейкой» — это односторонняя функция, для которой легко вычислить обратную, если известны некоторые особенности, используемые для создания функции. Как и лазейка, такие функции легко проходимы в одном направлении. Обратный процесс без специальной информации занимает невероятно много времени. Понятие «лазейки» будет применено в разделе 14.5.5, когда будет обсуждаться схема Меркла-Хэллмана (Merkle-Hellman).
14.5.3. Схема RSA
Сообщения в схеме Ривеста-Шамира-Дцельмана (Riyest- Shamir-Adelman -RSA) сначала представляются как целые числа из интервала (0, n-1). Каждый пользователь выбирает собственное значение п и пару положительных целых чисел е и d описанным ниже способом. Пользователь помещает свой ключ шифрования, числовую пару (п, е), в общедоступный каталог. Ключ дешифрования состоит из числовой пары (n, d), в которой d держится в секрете. Шифрование сообщения М и дешифрование шифрованного текста С определяются следующим образом.
Шифрование: С = Е(М) = (М)епо модулю n (14.32)
Дешифрование: М =D(C)= (C)d по модулю n
Это легко вычислить. Результатом каждой операции являются целые числа из интервала (0, n-1). В схеме RSA п получается в результате перемножения двух больших простых чисел р и q.
n=pq (14.33)
Несмотря на то что п общедоступно, p иq являются скрытыми из-за большой сложности в разложении п на множители. Затем определяется функция, называемая функцией Эйлера.
(14.34)
Параметр 
(п) имеет интересное свойство [12]: для любого целого X из интервала (0, n-1) и любого целого k имеет место, следующее соотношение.
по модулю n (14.35)
Следовательно, если все остальные арифметические действия выполняются по модулю п, арифметические действия в степени выполняются по модулю 
. Затем случайным образом выбирается большое целое число d, являющееся взаимно простым с ; это означает, что и d не должны иметь общих делителей, отличных от 1. Это записывается следующим образом.
НОД [, d]= 1 (14.36)
В данном случае НОД означает «наибольший общий делитель». Этому условию будет удовлетворять любое простое число, большее наибольшего из (р, q). Далее находится целое е, 0 < е <,
ed по модулю = 1, (14.37)
что, вследствие равенства (14.35), равносильно выбору е и d, которые удовлетворяют следующему условию.
X = Xed по модулю n (14.38)
Следовательно,
E[D(X)] = D[E(X)]=X (14.39)
и возможно корректное дешифрование. Один из возможных способов взлома шифра при данном ключе (п, е) — это разложить п на множители р и q, вычислить = (р-1)(q-1) и вычислить d из равенства (14.37). Все это, за исключением разложения п на множители, представляет собой простые действия.
Схема RSA основывается на том, что два больших простых целых числа р и q легко выбрать и перемножить, но гораздо сложнее разложить на множители результат. Следовательно, произведение, как часть ключа шифрования, может быть сделано общедоступным, в то время как множители, которые могут «разоблачить» ключ дешифрования, соответствующий ключу шифрования, остаются скрытыми. Если длина каждого множителя составляет порядка 100 разрядов, умножение может быть выполнено в доли секунды, а изнурительное разложение на множители результата может потребовать миллиарды лет [2].
14.5.3.1. Использование схемы RSA
Используя пример из работы [13], положим р=47, q=59. Следовательно, п- pq = = 1773 и = (р - 1)(q - 1) = 2668. Параметр d выбирается взаимно простым с . Например, выберем d=157. Затем вычислим значение е следующим образом (подробности приведены в следующем разделе).
ed по модулю = 1
157е по модулю 2688 = 1
Следовательно, е = 17. Рассмотрим пример открытого текста.
ITS ALL GREEK TO ME
Если заменить каждую букву двухразрядным числом из интервала (01, 26), соответствующим ее позиции в алфавите, и закодировать пробел как 00, открытое сообщение можно записать следующим образом.
0920 1900 0112 1200 0718 0505 1100 2015 0013 0500
Каждый символ выражается целым числом из интервала (0, п-1). Поэтому в данном примере шифрование может быть представлено в виде блоков по четыре разряда, так как это максимальное число разрядов, которое всегда дает число, меньшее п-1 = 2772. Первые четыре разряда (0920) открытого текста шифруются следующим образом.
С = (М)епо модулю п = (920)17 по модулю 2773 = 948
Продолжая этот процесс для оставшихся разрядов открытого текста, получим следующее.
С = 0948 2342 1084 1444 2663 2390 0778 0774 0229 1655
Открытый текст восстанавливается с помощью ключа дешифрования.
М = (С)157 по модулю 2773
14.5.3.2. Как вычислить е
Для вычисления е используется разновидность алгоритма Евклида вычисления НОД и d. Сначала вычисляем последовательность значений x0, x1, х2, ..., где x0 =, x1= d, а хi+1= хi-1 по модулю xi, пока не будет получено xk = 0. Тогда НОД (x0, x1) = хk-1. Для каждого xi вычисляются числа аi и bi, при которых хi= аi x0 + bi x1 . Если xk-1= 1, то bk-1 — мультипликативное обратное к х1по модулю х0. Если bk-1 — отрицательное число, решением является bk+1+.
Пример 14.5. Вычисление е с помощью d и
Для предыдущего примера, в котором р = 47, q = 59, п = 2773 и d выбрано равным 157, примените алгоритм Евклида для проверки, что е = 17.
Решение
|
i |
xi |
ai |
bi |
yi |
|
0 |
2668 |
1 |
0 |
|
|
1 |
157 |
0 |
1 |
16 |
|
2 |
156 |
1 |
-16 |
1 |
|
3 |
1 |
-1 |
17 |
Здесь
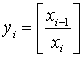
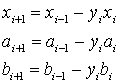
Следовательно,
e = b3=17.
14.5.4. Задача о рюкзаке
Классическая задача о рюкзаке изображена на рис. 14.19. Рюкзак наполнен множеством предметов с указанием их веса в граммах. Зная вес наполненного рюкзака (шкала весов градуирована так, что вес пустого рюкзака вычитается), нужно определить содержимое рюкзака. В этом простом примере решение легко найти методом проб и ошибок. Однако если в заданном множестве не 10, а 100 возможных единиц, задача может стать вычислительно неосуществимой.
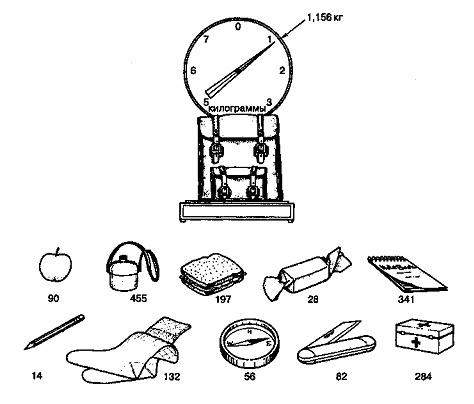
Рис. 14.19. Задача о рюкзаке
Опишем задачу о рюкзаке через вектор рюкзака и вектор данных. Вектор рюкзака представляет собой n-кортеж разных целых чисел (аналогично множеству разных предметов содержимого рюкзака).
a = a1, a2, …, an
Вектор данных — это n-кортеж двоичных символов.
x = x1, x2, …, xn
Рюкзак S — это сумма подмножества компонентов вектора рюкзака.
ax, где xi = 0,1 (14.40)
Задачу о рюкзаке можно сформулировать следующим образом: при данном S и известном а определите х.
Пример 14.6. Пример рюкзака
Дано а = 1, 2, 4, 8, 16, 32 и S = ах =26. Найдите х.
Решение
Видно, что в этом примере х — это двоичное представление S. Преобразование из десятичного в двоичное окажется более, знакомым, если представить а как 20, 21, 22, 23, 24, 25, 26. Вектор данных х находится легко, поскольку а в этом примере является быстровозрастающим; это означает, что каждый компонент набора n-кортежа а больше суммы предыдущих компонентов. Другими словами,
i = 2,3, ..., п (14.41)
Если а является быстровозрастающим, то первый элемент х - хn = 1, если S
аn (в противном случае, хn=0); следующий элемент находится согласно соотношению
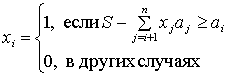, (14.42)
где i = п-1, п-2,..., 1. С помощью равенства (14.42) легко вычисляется х = 010110.
Пример 14.7. Пример рюкзака
Дано а = 171, 197, 459, 1191, 2410, 4517 и S = ах = 3798. Найдите х.
Решение
Как и в примере 14.6, а является быстровозрастающим. Поэтому с помощью равенства (14.42) можно вычислить х.
х = 010110
14.5.5. Криптосистема с открытым ключом, основанная на «лазейке» в рюкзаке
Эта схема, известная также как схема Меркла-Хэллмана [15], основана на образовании вектора рюкзака, который не является быстровозрастающим. Следовательно, задача не является легкоразрешимой. При этом данная задача о рюкзаке обязательно включает лазейку, позволяющую разрешенным пользователям решить задачу.
Сначала образуем быстровозрастающий п-кортеж. Затем выберем простое число М, при котором имеет место следующее неравенство.
(14.43)
Выберем также случайное число W (1<W<M) и сформируем W-1, удовлетворяющее следующему соотношению.
WW-1 по модулю М = 1 (14.44)
Вектор а' и числа М, W и W-1 удерживаются скрытыми. Затем из элементов а' формируем а.
ai= Waj’ по модулю М (14.45)
Формирование а с использованием равенства (14.45) — это создание вектора рюкзака с лазейкой. Если нужно передать вектор х, то вначале х умножается на а, что дает число S, которое передается через общедоступный канал. С помощью равенства (14.45) S можно записать следующим образом.
S = ах = 
(14.46)
Разрешенный пользователь получает S и, используя равенство (14.44), превращает его в S’.
= 
= 
(14.47)
Поскольку разрешенный пользователь знает засекреченный быстровозрастающий вектор а', для отыскания х он может использовать S'.
14.5.5.1. Использование схемы Меркла-Хэллмана
Предположим, пользователь А желает создать общедоступную и конфиденциальную функции шифрования. Сначала он рассматривает быстровозрастающий вектор а' = (171, 197, 459, 1191, 2410, 4517).
= 8945
Затем он выбирает простое число М, большее 8945, случайное число W, такое, что 1
W< М, и вычисляет W-1, при котором WW-1 = 1 по модулю М.
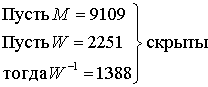
После этого он образует вектор, который оставляет «лазейку» в рюкзаке.
аi = аi’ 2251 по модулю 9109
а = 2343, 6215, 3892, 2895, 5055,2123
Пользователь А делает общедоступным вектор а, который, очевидно, не является быстровозрастающим. Предположим, что пользователь В желает послать сообщение пользователю А.
Если х = 010110 — сообщение, которое нужно передать, то пользователь В создает следующее число.
S = ах = 14 165 и передает его пользователю А
Пользователь А получает S и превращает его в S'.
S'= а'х = W-1S по модулю М= 1388
14 165 по модулю 9109 = 3798
Используя S' = 3798 и быстровозрастающий вектор а', пользователь А легко находит х.
Схема Меркла-Хэллмана сейчас считается взломанной [16], поэтому для реализации криптосистем с открытыми ключами используется алгоритм RSA (равно как и другие рассмотренные позднее).