8.1. Двойной интеграл
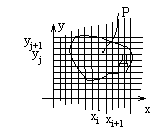
Пусть функция двух переменных z=f(x,y) – непрерывна на Д, где Д={(x,y)} – замкнутая область.
Разобьем эту область на прямоугольные части, как показано на рисунке.
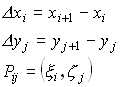
Вычислим объем параллелепипеда с основанием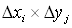 
и высотой 
:
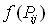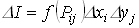- элементарный объем параллелепипеда.
Тогда двойным интегралом от функции f(x,y) по области Д называется предел интегральной суммы (суммарного объёма)
,
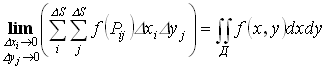если этот предел существует.
Теорема о существовании двойного интеграла
Если функция от x, y непрерывна в замкнутой области Д, то двойной интеграл существует и не зависит от способов разбиения и выбора точки в каждой элементарной области.
Геометрический смысл двойного интеграла – объем цилиндра, ограниченного снизу областью Д на плоскости (x, y), сверху поверхностью z = f(x, y).
Свойства двойного интеграла:
1)
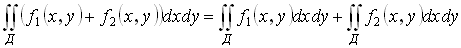
2)
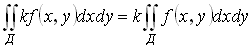
3)
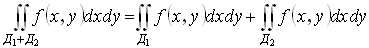
Вычисление двойного интеграла:
Пусть Д – правильная область, т.е. любая прямая, параллельная осям координат пересекает область не более, чем в двух точках
Пусть (соответственно рисунку) уравнения верхней и нижней граничных линий есть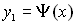 
и 
.
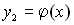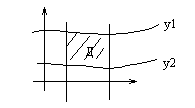Тогда двойной интеграл можно представить в виде повторного интеграла
.
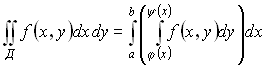Пример:
F(x, y)=x+ y
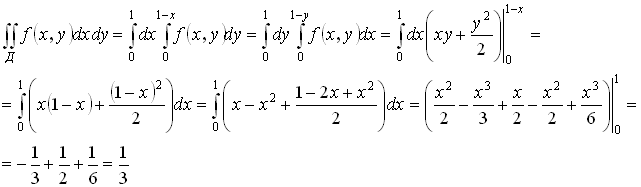
Для вычисления двойного интеграла формируется повторный интеграл (порядок интегрирования выбирается самостоятельно). Заметим, что пределы внутреннего интеграла могут зависеть только от внешней переменной.
Теорема об оценке двойного интеграла:
Пусть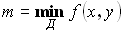 
и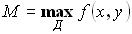 
. Тогда
.
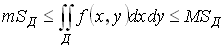Следствие: площадь области Д равна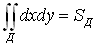 
Пример:
Пусть область Д ограничена линиями: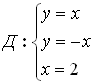
Интегрируемая функция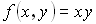 
. Тогда
.
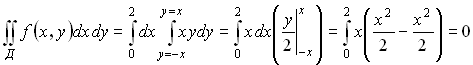8.2. Двойной интеграл в полярной системе координат
Формулы перехода от декартовой в полярную систему координат:
.
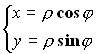Тогда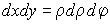 
. Двойной интеграл принимает вид:
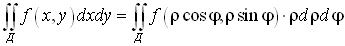
8.3. Тройной интеграл
Пусть функция трёх переменных u=f(x,y,z) непрерывна в V , где V – замкнутая, ограниченная область в пространстве.
Разобьем область V на части плоскостями, параллельными координатным плоскостям. В каждом полученном параллелепипеде выберем точку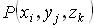 
и вычислим значение функции в этой точке 
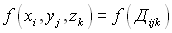. Составим интегральную сумму 
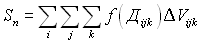, где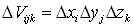 
.
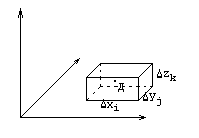
Переходя к пределу (если он существует), получим тройной интеграл:
.
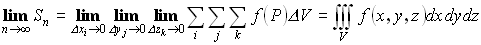Если функция непрерывна в замкнутой, ограниченной области, то тройной интеграл существует и не зависит от способа разбиения и выбора точки.
Свойства тройного интеграла:
1. Линейность
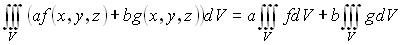
2. Аддитивность
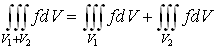. Здесь 
.
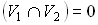3. Если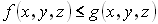 
на V
то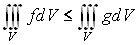 
Вычисление тройного интеграла:
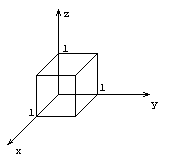
Пусть V – прямоугольный параллелепипед.
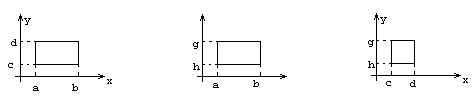
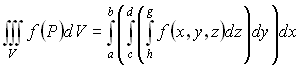- трехкратный повторный интеграл.
Пример:
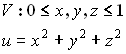
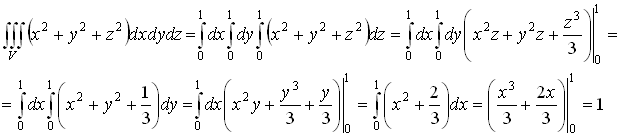
Пример:
V – произвольное тело (правильное)
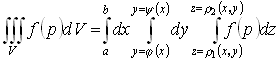
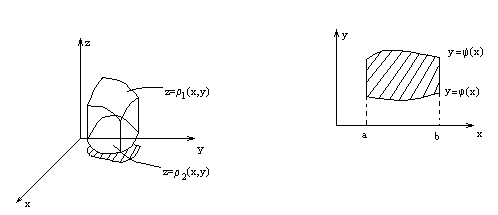
Вычисление тройного интеграла по произвольной области сводится к вычислению трехкратного повторного интеграла, причем внутренний интеграл берется между двумя ограничивающими поверхностями, средний – между двумя ограничивающими линиями, внешний – между двумя числами. Пределы интегрирования повторного интеграла не должны зависеть от внутренних переменных.
Пример:
u=f(x,y,z)
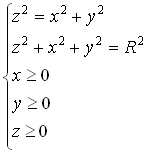
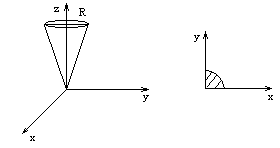
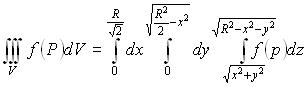
В этом примере удобно перейти в цилиндрическую систему координат.