4.2. Низкая вероятность обнаружения
4.3. Криптозащищенность сигнала
4.4. Электромагнитная совместимость
4.5. Эффекты распространения радиоволн в беспроводных системах
4.1. Помехоустойчивость
Окружающая обстановка, в которой конкретная система передает и извлекает информацию, не всегда полностью дружественна по отношению к ней. На приемной стороне полезному сигналу могут сопутствовать наряду с тепловым шумом и иные искажения различной природы. Следуя повсеместно принятой терминологии, будем называть подобные искажения помехами. Этот термин применяется повсеместно для учета непреднамеренного воздействия, обусловленного системами, работающими в том же или смежном частотном диапазоне, так и создаваемого преднамеренно как средства радиоэлектронного противодействия. Рассмотрим две основные модели помех, начав с узкополосной помехи.
4.1.1. Узкополосная помеха
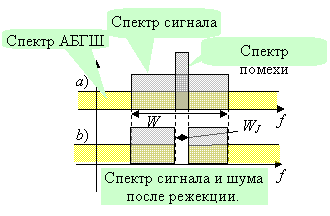
Данный тип помех наиболее характерен для ситуаций, когда некоторая соседствующая система или системы не имеют враждебных намерений по отношению к рассматриваемой, и создают помехи только как результат штатного функционирования. Предположим, что часть спектра сигнала подвергается воздействию не только АБГШ шума, но и помехи мощности J. Тогда спектр полезного сигнала, белого шума и помехи с полосой 
имеет вид, представленный на рисунке (a) справа. Назовем помеху узкополосной только по той причине, что занимаемая ею полоса 
уже полосы 
, занимаемой сигналом, и имеются области, где спектр сигнала не подвержен искажению помехой.
Предположим вначале, что рассматриваемая система не предпринимает никаких специальных мер для противодействия помехе за исключением, возможно, выбора подходящего сигнала. Подобного рода сценарий означает, что при проектировании возможность присутствия помехи принята в расчет на этапе выбора сигнала, однако система не подстраивает каждый раз закон модуляции сигнала и алгоритмы обработки под текущую помеховую обстановку. Другими словами, приемник системы всегда использует только фильтр, согласованный с АБГШ, невзирая на наличие или отсутствие помехи на входе. В первом приближении работа системы в этом случае характеризуется не классическим отношением сигнал-шум на выходе согласованного фильтра
,
а выходным отношением сигнал-(шум + помеха) 
, учитывающим наряду с АБГШ и деструктивное воздействие помехи. Для отыскания отношения сигнал-(шум + помеха) на выходе согласованного фильтра разделим выходную мощность сигнала 2EW на полную мощность 
отфильтрованных шума и помехи, поскольку последняя проходит через фильтр без всякого ослабления
Очевидно, что сигналы с широким спектром обладают иммунитетом к воздействию помехи. Поскольку 
, где P и T, как обычно, мощность и длительность сигнала соответственно, то при наложении ограничений на величину пиковой мощности сигнала (T не может быть уменьшено) существует только один способ повышения стойкости в отношении узкополосной помехи: использовать широкополосную стратегию.
Рассмотрим теперь иной сценарий, в котором система способна адаптировать приемник к текущей помеховой обстановке. При помехе, многократно превышающей естественный уровень АБГШ, оптимальная процедура обработки эквивалентна простому вырезанию частотного интервала спектра сигнала, в котором сосредоточена помеха. С этой целью используется полосовой режекторный фильтр, на выходе которого спектр сигнала и шума имеет вид, изображенный на рисунке (b). Подобный спектральный рисунок может трактоваться, как если бы исходный сигнал занимал лишь часть полосы , свободную от помех, и имел энергию 
. Тогда согласованный фильтр, очищая этот «остаточный» сигнал от АБГШ, обеспечивал бы выходное отношение мощностей сигнала и шума
которое снова свидетельствует о выгодах сигналов с широким спектром с точки зрения иммунитета к узкополосным помехам.
Итогом является следующий вывод: достижение высокой помехоустойчивости к узкополосной помехе без обращения к «грубой силе» (увеличению энергии и пиковой мощности) возможно только при расширении спектра сигнала независимо от его длительности, т.е. использовании широкополосной технологии.
4.1.2. Заградительная помеха
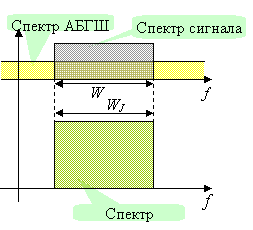
Во многих военных сценариях или приложениях, характерных для спецслужб, встречается ситуация, когда помеха создается преднамеренно как средство радиоэлектронного противодействия. В подобных случаях применяют так называемую заградительную шумовую помеху, спектр мощности которой покрывает спектр сигнала без пропусков 
(см. рисунок справа). Ясно, что заградительная помеха воздействует на сигнал как дополнительный АБГШ со спектральной плотностью мощности, равной 
. Поэтому отношение сигнал-(шум+помеха) по мощности после согласованного фильтра подавляемой системы
,
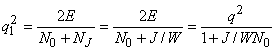В этом случае, однако, для нанесения большего вреда постановщик постарается обеспечить значительное превышение спектром помехи спектра естественного шума, т.е. 
, откуда следует, что
.
Вновь можно констатировать, что при лимите как пиковой мощности полезного сигнала, так и мощностного ресурса постановщика помех, единственным способом повышения иммунитета системы к заградительной помехе является привлечение сигналов с большим значением частотно-временного произведения 
, т.е. широкополосных сигналов.
Последняя формула объясняет другое популярное название частотно-временного произведения . Как видно, отношение мощностей сигнала и шума с равномерным спектром в полосе сигнала увеличивается согласованным фильтром в 
раз по сравнению со входным значением 
. Таким образом, можно назвать выигрышем от обработки.
4.2. Низкая вероятность обнаружения
При радиоэлектронном противодействии эффективная помеха может быть организована только после обнаружения присутствия противостоящей системы в эфире и оценки таких ее параметров как несущая частота и ширина спектра. Поэтому широко распространен сценарий конфронтации двух систем, при котором первая (назовем ее защищаемой) старается действовать по возможности скрытно и предотвратить обнаружение своего сигнала, тогда как вторая (перехватчик) находится в постоянной готовности, предпринимая все меры для обнаружения активной работы первой. Принимая сторону защищаемой системы, исследуем возможности широкополосной передачи в плане обеспечения скрытности и низкой вероятности обнаружения присутствия сигнала в эфире.
Предположим, что защищаемая система использует сигнал с некоторым замысловатым законом модуляции, детали которого неизвестны перехватчику, не давая последнему шанса применить согласованный фильтр или коррелятор для обнаружения сигнала. При этом естественно полагать, что у перехватчика нет иного выбора, как считать перехватываемый сигнал случайным и пытаться обнаруживать его только по признаку появления или отсутствия некоторого избытка энергии в сканируемом участке частотного диапазона. Таким образом, энергетический приемник (радиометр), являющийся оптимальным при обнаружении ограниченного по полосе шумового сигнала на фоне АБГШ, принимается в качестве рабочего инструмента перехватчика. На нижеприведенном рисунке показана структура энергетического приемника.
Полосовой фильтр с полосой 
, пропускающей весь спектр сигнала или только его часть, фильтрует наблюдение с целью устранения внеполосного шума. Квадратичный амплитудный детектор осуществляет оценку мгновенной мощности, которая в дальнейшем интегрируется для выработки оценки энергии 
в пределах интервала наблюдения 
. Полученная оценка энергии сравнивается затем с порогом 
, и при выполнении неравенства 
принимается решение о наличии в наблюдении сигнала наряду с естественным шумом, тогда как непревышение порога трактуется как признак отсутствия сигнала. Качество работы приемника перехватчика будет главным образом зависеть от показателей энергетического приемника, настроенного на истинную частотно-временную зону перехватываемого сигнала. Это позволяет идеализировать априорную осведомленность перехватчика и предполагать, что ему известно, где в плоскости время-частота концентрируется энергия обнаруживаемого сигнала. Поскольку наблюдение вне длительности сигнала не содержит информации о его присутствии, можно положить 
.
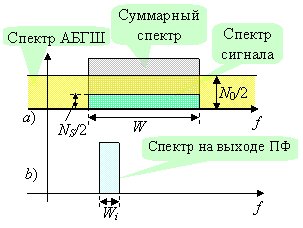
На рисунке справа представлена прямоугольная аппроксимация спектра сигнала вместе с равномерной спектральной плотностью мощности естественного АБГШ (a) и амплитудно-частотной характеристикой полосового фильтра радиометра (b). С точки зрения перехватчика указанием на присутствие сигнала служит избыточная (сигнальная) спектральная плотность мощности 
, добавляемая сигналом к спектральной плотности мощности теплового шума 
.
Поскольку выходное напряжение 
квадратичного детектора равняется мгновенной входной мощности, то отношение сигнал-шум по напряжению на его выходе определится как
,
где 
и 
– соответственно мощность сигнала и шума на выходе полосового фильтра.
Для сглаживания случайных флюктуаций постоянной составляющей напряжения на выходе детектора на интервале наблюдения 
производится накопление 
статистически независимых отсчетов, так что результирующее отношение сигнал-шум на входе компаратора составит величину
.
Очевидно, что перехватчик, заинтересованный в максимизации характеристики приемника, должен выбрать ширину полосы пропускания ПФ максимально возможной, т.е. равной полосе сигнала: 
, обеспечивая наибольшее отношение сигнал-шум
,
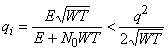где 
, как и ранее, отношение сигнал-шум на выходе согласованного фильтра приемника защищаемой системы.
Очевидно, что 
должно быть достаточно большим, поскольку в противном случае защищаемая система не сможет нормально функционировать. Ясно также, что у защищаемой системы имеется единственная возможность снизить риск обнаружения своего сигнала потенциальным перехватчиком: использовать широкополосный сигнал с максимально возможным частотно-временным произведением , обеспечивая 
. Возвращение к ранее приведенному рисунку позволяет физически обосновать подобное заключение. Расширение спектра сигнала при постоянстве энергии и длительности снижает его спектральную плотность мощности 
, маскируя ее под спектром естественного теплового шума, так что
.
В заключении еще раз подчеркнем, что действенным (фактически единственным) путем достижения высокой скрытности является использование широкополосной технологии.
Пример 4.2.1. Для надежной передачи цифровых данных вполне адекватным является отношение сигнал-шум 
(14 дБ). При использовании широкополосных сигналов с 
отношение сигнал-шум для приемника перехватчика оказывается 
(–8 дБ), что совершенно недостаточно для надежного обнаружения сигнала защищаемой системы. Не составляет труда убедиться, что если перехватчик готов мириться с вероятностью ложной тревоги 
, то вероятность правильного обнаружения составит 
, т.е. окажется чрезвычайно малой и не представляющей серьезной угрозы скрытности защищаемой системы.
Завершая параграф, отметим, что выгоды, связанные со скрытностью распределенного спектра, в наши дни широко эксплуатируются не только военными потребителями и спецслужбами. То обстоятельство, что широкополосный сигнал практически незаметен для оборудования систем радиоконтроля, серьезным образом влияет на лицензионную политику. В частности, рынок коммерческих систем, имеющих право выхода в эфир без получения лицензии, постоянно расширяется, и во многих регионах выделены специальные частотные диапазоны для подобного безлицензионного использования.
4.3. Криптозащищенность сигнала
Продолжая линию предыдущего параграфа, напомним, что единственной причиной, вынуждающей перехватчик использовать столь неэффективный инструмент как энергетический приемник, является отсутствие информации о тонкой структуре обнаруживаемого сигнала, т.е. его законе модуляции. По этой причине перехватчик не может обрабатывать сигнал по тем же алгоритмам, что и приемник защищаемой системы (т.е. осуществлять согласованную фильтрацию). Понятно, что при выборе закона модуляции из немногочисленного набора альтернатив, априорно известных перехватчику, последний может разгадать фактически использованную структуру сигнала с помощью простого перебора. Таким образом, важным фактором противоборства защищаемой системы с перехватчиком является применение сигналов с криптозащищенной (практически не поддающейся расшифровке) структурой.
Подобная задача весьма характерна и для защищаемых военных и коммерческих систем, постоянно присутствующих в эфире и потому не особенно озабоченных сокрытием самого факта активного функционирования. Первоочередным требованием для них является минимизация риска несанкционированного доступа к обслуживанию, адресованному лишь авторизованным пользователям, или фальсификации передаваемой информации.
В дисциплинах, связанных с информационной безопасностью, степень защиты данных определяется числом равновероятных конкурирующих ключей, которые криптоаналитик противной стороны должен перепробовать в попытке взломать шифротекст, т.е. засекреченные данные. В применении к структуре сигнала каждый из таких ключей есть не что иное, как конкретный закон модуляции, который обычно повторяется с некоторым периодом . Предположим, что сигнал построен из чипов (см. пример в 1.5.3) на основе 
-ичного алфавита, т.е. с использованием -символьной манипуляции чипов. Если полоса, отводимая системе, равна , то общее сигнальное пространство имеет размерность , т.е. закон модуляции можно считать сконструированным из чипов. Очевидно, что величина 
определяет общее число различных законов модуляции, т.е. конкурирующих ключей, и, значит, системный дизайнер в стремлении к высокой степени секретности модуляционного формата, должен ориентироваться на сигналы с достаточно большим частотно-временным произведением.
Заключением к дискуссии параграфа может служить следующий тезис: широкополосная технология весьма полезна в аспекте криптозащиты структуры сигнала.
Пример 4.3.1. Сигнал P-канала (P–код) в системе GPS является бинарным 
с полосой 
МГц. Его закон модуляции имеет регулярный характер и повторяется с периодом в семь суток. Будучи «спрятанным» под тепловым шумом, этот сигнал не может быть восстановлен путем посимвольного приема и только знание его тонкой структуры позволило бы эффективно очистить его от АБГШ. Чтобы предотвратить несанкционированный доступ к P-коду последний суммируется по модулю два с секретным ключом (W-кодом), маскирующим структуру результирующего Y-кода. Один символ W-кода перекрывает 20 символов P-кода, так что для взлома ключа перебором пришлось бы протестировать до 
вариантов. Так как 
, число проверяемых ключей больше чем два в степени десять миллиардов, т.е. невообразимо велико. По этой причине Y-код считается практически застрахованным от взлома, и в течение всей истории GPS случаи успешных криптоаналитических атак на него не засвидетельствованы.
4.4. Электромагнитная совместимость
Проблема электромагнитной совместимости (ЭМС) является одной из наиболее животрепещущих для современных беспроводных технологий. ЭМС подразумевает бесконфликтное сосуществование различных систем в эфире, несмотря на то, что каждая из них принимает не только свой собственный сигнал, но и сигналы остальных систем и в задачу системного разработчика входит минимизация потенциального вреда от подобного воздействия. К числу традиционных способов обеспечения ЭМС относятся детальное частотное планирование под контролем национальных и международных инстанций, использование узконаправленных антенн, улучшение избирательности радиочастотных трактов приемников и др. Приведенные ниже простые рассуждения показывают, что применение широкополосных сигналов может быть также внесено в этот список.
В части излучающей системы следующая логика представляется оправданной. Поскольку существует возможность сделать сигнал практически незаметным даже для специальных приемников радиомониторинга за счет усложнения закона модуляции (см. параграф 4.2), т.е. расширения спектра, подобный сигнал тем более не окажет вредного влияния на обычную принимающую систему, работающую в том же диапазоне. Задача состоит лишь в выборе такого частотно-временного произведения , которое позволило бы удержать спектральную плотность мощности на входе принимающей системы ниже заданного порога. Как самое грубое приближение примем за «достаточно низкий» уровень в 
дБ по отношению к тепловому шуму, что для сигнала с энергией E, мощностью P и выигрышем от обработки WT означает
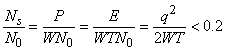или 
,
где снова целевой параметр определен в терминах отношения сигнал-шум «своего» приемника и выигрыша от обработки . Если бы, например, отношение сигнал-шум излучающей системы в точке расположения принимающей системы было 20 дБ, то величину 
можно было бы считать удовлетворительной в смысле ЭМС.
С позиций принимающей системы любой сигнал, пришедший от сторонней излучающей, может трактоваться как узкополосная или широкополосная помеха, и все аргументы в пользу широкополосности в борьбе с помехами (см. 4.1) дословно приложимы и к рассматриваемой задаче. Тем самым, широкополосная технология оказывается одним из действенных средств обеспечения ЭМС.
4.5. Эффекты распространения радиоволн в беспроводных системах
Проблемы, связанные с распространением волн в физических средах, достаточно сложны и нередко с трудом поддаются теоретическому анализу. Имеет место большое разнообразие факторов, вызывающих как детерминированное, так и случайное ослабление сигнала, достигающего приемной стороны. Как результат их воздействия принимаемый сигнал искажается не только аддитивным шумом (АБГШ), но и мультипликативной помехой, название которой вытекает из того факта, что она меняет интенсивность сигнала, т.е. перемножается с его амплитудой.
Начнем с идеализированной модели распространения в свободном пространстве, где отсутствуют препятствия между передающей и приемной антеннами, и излученная волна распространяется по единственно возможному пути, называемому линией прямой видимости (ЛПВ). Тогда на основе элементарной геометрии мощность принятого сигнала 
может быть предсказана с помощью формулы Фрииза:
,
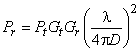где 
– мощность излученного сигнала, 
и 
– коэффициенты усиления передающей и приемной антенны соответственно, 
– длина волны несущего колебания, а D – расстояние между передатчиком и приемником. Как показывает последняя формула, ослабление мощности сигнала вдоль линии прямой видимости в свободном пространстве обратно пропорционально квадрату расстояния.
Модель распространения в свободном пространстве можно непосредственно использовать в расчетах линий связи, где окружающую обстановку можно уподобить открытому пространству, например, между космическими объектами или летательными аппаратами, наземным центром контроля и спутником и т.п. Среда распространения наземных систем намного менее благоприятна и главными факторами влияния на интенсивность сигнала оказываются затенение и многолучевой фединг (замирание).
Затенение обусловлено деталями ландшафта, препятствующими прямолинейному распространению: возвышенностями, растительностью, постройками и т.п. Вследствие их влияния интенсивность сигнала падает с расстоянием значительно быстрее, чем предсказывает формула Фрииза. Очевидно, что нерегулярный характер земных ландшафтов делает невозможной или бесполезной попытку создания некоторой универсальной теоретической модели затенения. Предложен целый ряд эмпирических моделей возможных зависимостей между принимаемой мощностью и длиной пути распространения. Среди специалистов в области мобильной связи одной из наиболее приемлемых признана модель Окамуры–Хаты (Ocumura-Hata). Согласно последней зависимость средней принятой мощности 
подчиняется равенству
,
в котором конкретное значение показателя 
зависит от типа подстилающей поверхности, изменяясь от 3 (сельская местность) до 5 (плотная городская застройка), а коэффициент 
– определяется частотным диапазоном и высотой антенн.
Принятая мощность, рассчитанная таким образом, дает лишь очень грубую отправную цифру, соответствующую усреднению по различным положениям приемника, равноудаленным на 
от передатчика. Флюктуации 
по дуге радиуса с центром в месте расположения передатчика значительны и часто аппроксимируются логнормальным законом, означающим, что распределение принятой мощности в децибелах 
, является гауссовским (нормальным):
.
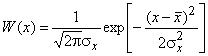Среднеквадратическое отклонение
величины 
обычно принимается лежащим в пределах от 6 до 12 дБ.
Затухание сигнала, обусловленное затенением, носит статический характер и даже для движущегося приемника принятая мощность меняется во времени сравнительно медленно в связи с относительно большой пространственной протяженностью элементов ландшафта (десятки-сотни метров). По этой причине затенение иногда фигурирует и под такими названиями, как крупномасштабные или долговременные замирания (фединг).
Рассмотрим теперь второй фактор, влияющий на интенсивность принимаемого сигнала: многолучевое распространение. В реальности излученный сигнал может достичь приемной антенны разнообразными путями. Прямой путь может оказаться одним из них, но может быть и полностью блокирован, тогда как все остальные пути обязаны своим происхождением рефракции волн, и, что гораздо характернее, отражению излученной волны различными объектами. Подобными отражателями могут оказаться здания, заводские трубы, воздушные суда, подстилающая поверхность и многое другое (см. рисунок).
Предположим, что, распространяясь по 
-му пути, переданный сигнал с комплексной огибающей 
приобретает амплитуду 
, задержку 
и начальную фазу 
. Тогда комплексная огибающая принятого сигнала запишется как
,
где, без потери общности, действительная амплитуда исходного сигнала принята равной единице.
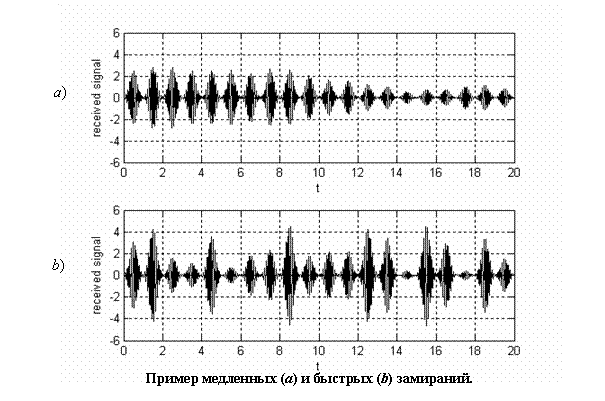
В том случае, когда диапазон рассеяния по задержке 
, т.е. максимальное значение взаимной задержки между сигналами различных путей, не превосходит длительности сигнала, все многолучевые реплики перекрываются и интерферируют между собой. Хаотичность распределения отражателей или рассеивателей на пути распространения волн придает интерференционной картине непредсказуемый характер: мощность результирующего сигнала может, как возрастать, если фазы сигналов отдельных путей близки, так и спадать, если они противоположны (см. рисунок). Именно этот феномен и получил название многолучевого фединга (замирания, обусловленного многолучевым распространением), которому присваивают и другие названия: мелкомасштабный или кратковременный фединг. Причины, обуславливающие подобные наименования, поясняются примером.
Пример 4.5.1. Пусть излученный сигнал поступает на приемник по путям, созданным двумя отражателями (зданиями, машинами и т.п.), а прямой путь (ЛПВ) полностью блокирован препятствием (зданием). Отражатели ориентированы в пространстве таким образом, что излучаемые ими вторичные волны распространяются навстречу друг другу (см. рисунок слева на следующем слайде).
На входе приемника, расположенного на линии, соединяющей отражатели, будет наблюдаться суперпозиция двух интерферирующих колебаний, которая образует стоячую волну с периодом 
. Двигаясь вдоль оговоренной линии, приемник будет наблюдать чередование максимумов и минимумов амплитуды с периодом метров. Если амплитуды отраженных сигналов близки по величине (что вполне вероятно), то результирующая мощность спадает почти (или в точности) до нуля, когда приемник проходит узлы стоячей волны. Поскольку пространственное расстояние между соседними пиками сравнимо с длиной волны, то для систем, работающих в метровом и дециметровом диапазонах, временные циклы изменения на входе мобильного приемника будут достаточно короткими (обычно доли секунды).
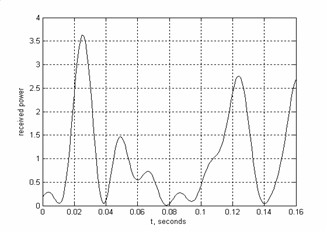
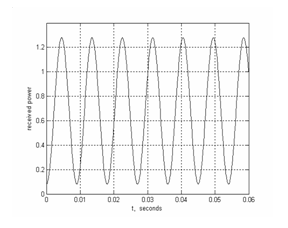
График зависимости от времени, представленный на рисунке справа, отвечает значениям параметров, характерным для мобильной связи: 
м и скорости носителя приемника 
км/час. Как видно из диаграммы, даже при относительно невысокой скорости принимаемая мощность меняется достаточно быстро.
Разумеется, приведенный пример искусственно упрощен с тем, чтобы представить исследуемый эффект наиболее наглядно. В действительности, число одновременно принимаемых многолучевых сигналов 
может быть очень большим, делая интерференционную картину гораздо более сложной. Характерная временная зависимость принимаемой мощности на входе приемника мобильного телефона представлена на рисунке справа, которая наглядно демонстрирует нерегулярный характер изменения мощности, как и наличие глубоких провалов в интенсивности принимаемого сигнала.
Убедится в том, что эффект замираний носит весьма деструктивный характер, можно на примере передачи бинарных данных по каналу с быстрыми замираниями. При отсутствии замираний (стабильности энергии сигнала E, т.е. отношения сигнал-шум q) вероятность ошибки на бит определяется соотношением
.
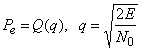Если амплитуда 
принятого сигнала случайна и меняется от одного сеанса приема к другому, то энергия сигнала для некоторого конкретного значения амплитуды составит 
, где 
– энергия эталонного сигнала, отвечающая случаю 
. Удобна нормировка, полагающая средний квадрат амплитуды флуктуирующего сигнала, равным единице, поскольку в этом случае средняя энергия совпадает с энергией эталонного сигнала
.
Тогда при фиксированной и равной амплитуде сигнала отношение сигнал-шум 
и условная вероятность ошибки 
становятся равными
.
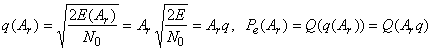Отметим, что среднее значение отношения сигнал-шум по мощности совпадает со значением отношения сигнал-шум 
для эталонного сигнала:
.
При флуктуирующем по амплитуде сигнале естественно принять за показатель качества коммуникационной системы значение , усредненное по всем
,
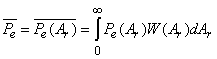где 
– плотность распределения вероятности случайной амплитуды . Подобное усреднение особенно оправдано в случае быстрых флюктуаций, когда в течение одной сессии приема уровень сигнала меняется много раз (см. рисунок).
Одной из наиболее достоверных моделей быстрых флюктуаций является модель, описываемая законом Рэлея:
где использована ранее упомянутая нормировка среднего квадрата . График плотности вероятности Рэлея приведен на рисунке.
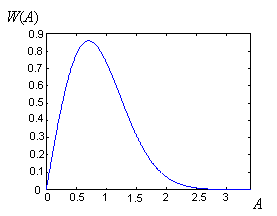
Правомерность применения рэлеевской модели базируется на центральной предельной теореме. Плотность вероятности суперпозиции примерно независимых и близких по вкладу случайных слагаемых стремится к гауссовской по мере роста их числа. Следовательно, интерференция множества пришедших по разным путям сигналов, подчиняющихся названным условиям, порождает на входе приемника гауссовский радиопроцесс. Если среди входных компонентов отсутствует доминирующая детерминированная составляющая (подобная ЛПВ сигналу), результирующий гауссовский процесс будет иметь нулевое среднее. Огибающая же такого процесса подчиняется рэлеевскому распределению и, таким образом, приходим к модели канала с рэлеевскими замираниями.
Осуществив усреднение, получаем
.
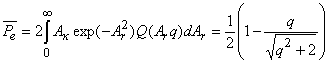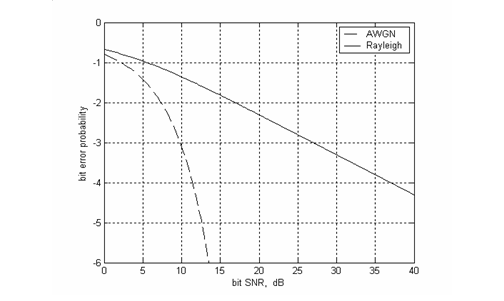
Количественно оценить масштаб вреда от замираний можно с помощью рисунка, на котором представлены вероятности ошибки передачи БФМ сигналов по гауссовскому (пунктир) и рэлеевскому (сплошная линия) каналам. Как следует из графиков, вероятность ошибки 
гарантируется для АБГШ канала при отношении сигнал-шум на бит близком к 10 дБ, тогда как для рэлеевского канала подобная достоверность передачи возможна лишь при отношении сигнал-шум не менее 27 дБ, т.е. большем в 50 раз. Столь внушительные энергетические потери от замираниями, становятся еще большими при ужесточении требований к надежности передачи и близки к 25 дБ (300 раз) при 
.
4.6. Разнесение
Основная идея борьбы с деструктивными эффектами многолучевости заключается в использовании разнесения, состоящего в организации нескольких независимых каналов или ветвей передачи. Хотя каждая из ветвей при этом по-прежнему подвержена рэлеевским (или другим) замираниям, вероятность того, что интерференционные картины во всех из них будут одновременно неблагоприятными, определяется правилом умножения вероятностей и, таким образом, существенно меньше вероятности «плохого» состояния индивидуальной ветви. Например, если каким-либо способом организованы две независимые идентичные ветви и вероятность возникновения неблагоприятных условий распространения в одной из них равна 0.1, то вероятность одновременного спада интенсивности сигнала в обеих будет 0.01, т.е. станет заметно меньше. С увеличением количества ветвей подобный выигрыш от разнесения становится все более и более заметным. Работая параллельно, ветви как бы подстраховывают друг друга, смягчая последствия замираний.
В зависимости от способа организации независимых каналов передачи выделяют несколько традиционных методов разнесения.
4.6.1. Пространственное (антенное) разнесение
Возникновение быстрых замираний обусловлено случайностью фазовых сдвигов многолучевых сигналов, что, в свою очередь, вызвано случайностью расположения отражателей, порождающих различные пути распространения. Как правило, фазовые диаграммы в двух точках пространства, разнесенных более чем на 7…10 длин волн, могут рассматриваться как независимые. Следовательно, отделенные в пространстве друг от друга расстоянием в 7…10 длин волны или более, две или несколько приемных антенн обеспечат практическую независимость параллельных интерференционных картин на приемной стороне, а значит каналов передачи (см. рисунок на следующем слайде).
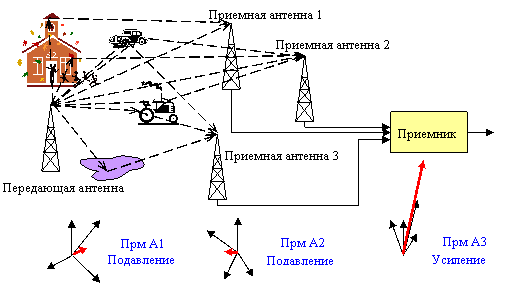
После индивидуальной согласованной фильтрации сигналы с выхода своей антенны могут быть скомбинированы согласно алгоритму селекции ветви с максимальным сигналом или по максимуму отношения сигнал-шум (взвешенное суммирование, обеспечивающее максимально возможное результирующее отношение сигнал-шум).
Параллельные антенны можно использовать также и на передающей стороне, однако в этом случае ограниченный ресурс полной мощности передатчика приходится дробить между несколькими передающими антеннами, что снижает энергопотенциал каналов разнесения. Тем не менее разнесение на передаче в некоторых ситуациях может оказаться выгодным. Так этот метод разнесения используется базовыми станциями систем мобильного телефона третьего поколения.
Метод разнесения на приеме, несомненно, является очень эффективным и широко практикуемым инструментом (например, он используется базовыми станциями системы мобильного телефона в канале «вверх»), однако не является универсальным. Так он с трудом может быть применен в мобильных приемниках (т.е. в канале «вниз») из-за малых размеров трубок.
4.6.2. Частотное разнесение
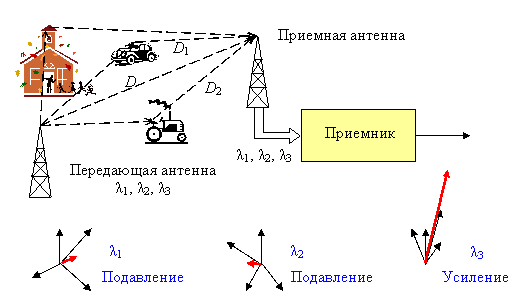
Идея частотного разнесения связана с понятием полосы когерентности канала. Эта величина характеризует максимальную ширину частотного интервала, в пределах которого фединг может считаться плоским, т.е. замирания гармоник сигнала практически стопроцентно зависимы. При этом замирания гармоник, разделенных по частоте интервалом, превышающим полосу когерентности, принимаются за независимые. Очевидно, что одновременная передача одного и того же сигнала несколькими несущими, частоты которых разнятся на полосу когерентности или более, образует ряд ветвей разнесения. Следующий рисунок дает элементарное толкование этому методу разнесения.
Частотный интервал плоского фединга обратно пропорционален диапазону рассеяния по задержке , так что чем сильнее рассеяние многолучевых сигналов по времени, тем уже полоса когерентности. Так, для систем мобильной связи типичной является величина 
мкс, что соответствует полосе когерентности близкой 50 КГц. Тогда для организации разнесения по частоте несущие должны выбираться со сдвигом не меньшим 50 КГц. Отметим, что аналогично разнесению на передаче частотное разнесение также предполагает дробление ресурса полной излучаемой мощности (теперь между несущими), что тем не менее оказывается продуктивным. Примером использования разнесения по частоте служит система мобильного телефона GSM.
4.6.3. Временное разнесение
Временное разнесение базируется на флюктуациях многолучевого профиля во времени. Даже тогда, когда приемник неподвижен, интерференционная картина может меняться со временем из-за движения передатчика или окружающих отражателей. Вследствие этого возникает доплеровское рассеяние принимаемого сигнала, и чем шире его разброс, тем меньше время когерентности канала, т.е. интервал времени, в течение которого мощность результирующего многолучевого сигнала остается примерно постоянной. Вновь обращает на себя внимание дуальность частоты и времени: интервал корреляции в частотной области (полоса когерентности) обратно пропорционален диапазону рассеяния по задержке, тогда как аналогичный интервал во временной области (время когерентности) обратно пропорционален диапазону частотного (доплеровского) рассеяния. Поскольку в моменты, разделенные временем когерентности или более, многолучевые интерференционные картины можно считать независимыми, повторная передача нескольких копий одного и того же сообщения с соответствующим интервалом создает ряд ветвей разнесения. С некоторой адаптацией этот принцип используется в телекоммуникационных системах в форме процедуры перемежения совместно с корректирующими кодами. Для разнесения во времени символов некоторого кодового слова на интервал, превышающий время когерентности, производится перемешение символов группы следующих друг за другом кодовых слов. В результате поражающий данное кодовое слово пакет ошибок, обусловленный замиранием, распределяется между рядом слов в виде независимых, а модель канала трансформируется в модель без памяти. Подобная форма разнесения во времени реализована в системах мобильной связи стандарта GSM и IS-95 как в прямом, так и обратном канале. Однако сопутствующая этому методу задержка в передаче может существенно ограничить его применимость.
4.6.4. Многолучевое разнесение
Метод многолучевого разнесения уникален в том смысле, что он радикально меняет отношение к эффектам многолучевости, которые на первый взгляд представляются безоговорочно вредными. В самом деле, любой отражатель, причастный к приему сигнала, направляет к приемнику часть излученной энергии, которая в его отсутствие была бы безвозвратно потеряна. В обстоятельствах, когда соответствующе отраженные сигналы могут быть отделены друг от друга (разрешены во времени), их энергию можно использовать для улучшения характеристик системы в сравнении со случаем отсутствия многолучевости. Многолучевой канал как будто сам создает ветви разнесения, и единственной проблемой является адекватный выбор сигнала, который позволил бы разделить сигналы разных лучей.
Пусть время корреляции сигнала 
, т.е. протяженность его АКФ, не превышает минимальной взаимной задержки между последовательными во времени многолучевыми сигналами 
. Очевидно, что в такой ситуации все многолучевые сигналы после согласованного фильтра не перекроются и полностью разрешаются во времени, не мешая друг другу.
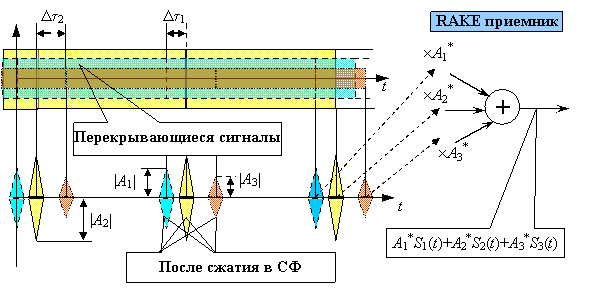
Ясно, что для применимости схемы многолучевого разнесения сигнал должен иметь узкую АКФ. Возвращаясь к дискуссии раздела 3.1, можно вспомнить, что лобовое решение этой задачи состоит в использовании коротких сигналов. Подобный путь, однако, предполагает излучение сигналов с высокой пиковой мощностью, что может оказаться неприемлемым во многих приложениях. Значительно более изящной представляется ориентация на широкополосные сигналы с 
. В этом случае вложение необходимой энергии происходит при умеренной пиковой мощности, что обеспечивается за счет большой длительности сигнала, тогда как разрешение во времени достигается после временной компрессии в согласованном фильтре. Рисунок на следующем слайде иллюстрирует подобный подход при передаче данных с бинарной ФМ.
Пусть требуемая скорость передачи составляет 
бит/сек. Возьмем широкополосный сигнал 
длительности 
и будем отображать каждый бит обычным для бинарной ФМ способом. Передача нулевого значения бита осуществляется прямым сигналом , а единичного – инверсией сигнала 
. При полосе 
и правильно синтезированном сигнале все многолучевые копии не будут перекрываться после временного сжатия в согласованном фильтре. Их комбинирование с учетом полярности (например, по методу с максимальным отношением) обеспечит более высокое качество, чем при использовании только одного из многолучевых сигналов, например, сигнала прямой видимости.
Реализованный подобным образом прием многолучевых сигналов называется RAKE («грабли») алгоритмом, поскольку пики на выходе согласованного фильтра напоминают в некоторой степени зубцы этого популярного садового инструмента. По этой причине каждый отдельный отклик фильтра получил наименование пальца. RAKE алгоритм с 3-мя и более пальцами применяется как в прямом, так и в обратном канале системы мобильного телефона стандарта IS-95. Проекты систем мобильной связи 3-го поколения также ориентированы на утилизацию достоинств RAKE приемников.
С точки зрения рассмотренной проблемы уместно ввести еще один термин: коэффициент расширения. Использование его для обозначения частотно-временного произведения типично для цифровых систем связи. Происхождение данного термина объясняется тем, что произведение 
показывает во сколько раз расширена полоса сигнала по сравнению с передачей данных простым сигналом.
Завершая данный параграф, в перечень достоинств технологии расширенного спектра может быть добавлено еще одно: возможность организации многолучевого разнесения.